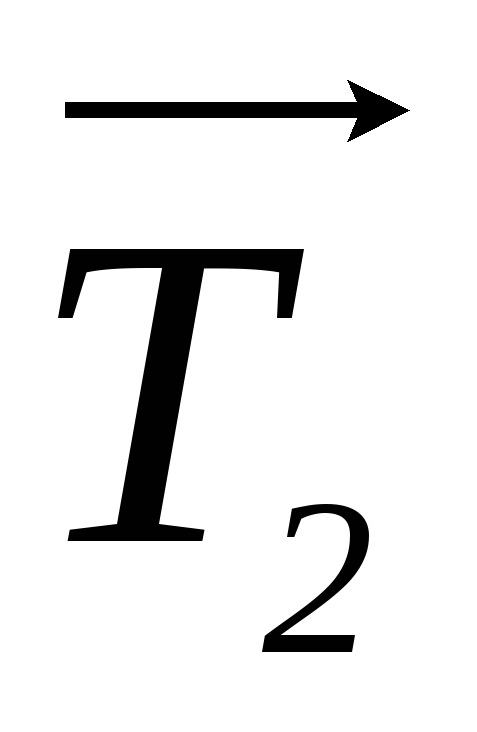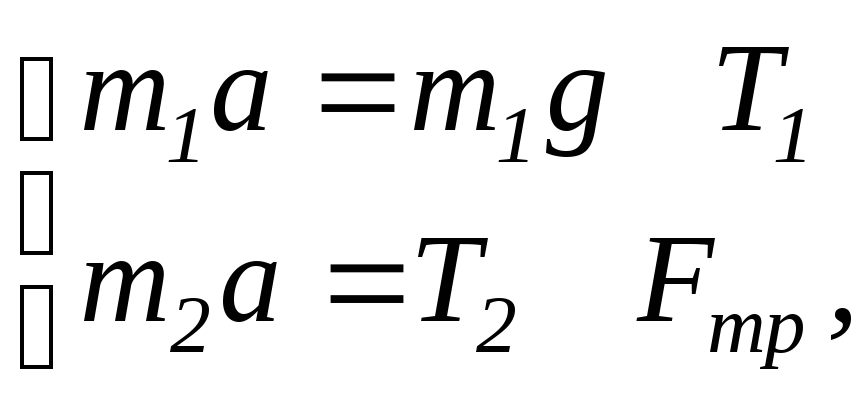Динамика вращательного движения
Основные законы и формулы
1. При криволинейном движении сила, действующая на материальную точку, может быть определена по формуле
где 

Если касательная составляющая равнодействующей силы, действующей на точку, 

2. Между двумя точечными телами массами m1 и m2, находящимися на расстоянии r друг от друга, действует сила тяготения, которая определяется законом всемирного тяготения:
где γ – гравитационная постоянная: γ≈6,67∙10-11 Н∙м2/кг2.
3. Для характеристики вращательного движения твердых тел часто пользуются моментом М силы F относительно оси вращения.
Момент М является векторной величиной. Величина момента М некоторой силы F относительно оси вращения определяется формулой:
где l – расстояние от оси вращения до прямой, вдоль которой действует сила.
4. Основное уравнение динамики вращательного движения:
а) в общем случае
М
где М – момент силы, действующей на тело в течении времени dt, J – момент инерции тела, 

б) в случае постоянных момента силы и момента инерции
в) в случае постоянного момента инерции
где 
5. Момент импульса материальной точки
где m – масса точки, 
Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси z:

где Jz – момент инерции системы тел относительно оси z; 
6. Момент инерции материальной точки:
где m – масса точки; r – расстояние до оси вращения.
Моменты инерции некоторых тел массой m относительно оси z, проходящей через центр масс:
а) стержня длиной l относительно оси, перпендикулярной стержню:
б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра):
где R – радиус обруча (цилиндра);
в) диска или сплошного цилиндра радиусом R относительно оси, перпендикулярной плоскости основания:
г) однородного шара радиуса R относительно оси, проходящей через его центр:
где 

Общее условие равновесия тела гласит, что для того, чтобы тело находилось в равновесии, необходимо, чтобы были равны нулю равнодействующая приложенных к телу сил и сумма моментов этих сил относительно оси вращения:
F

Примеры решения задач


Решение. В данном случае нормальные ускорения шариков вызваны действием сил натяжения Т1 и Т2. Поскольку шарики не смещаются относительно оси вращения, то Т1=Т2. Согласно второму закону Ньютона, можно записать:
Сила натяжения нити будет равна:

Решение. На шарик действуют: mg – сила тяжести, Т- сила натяжения нити (рис.8). Запишем для шарика уравнение второго закона Ньютона в векторной форме: Рис. 8
Спроецируем это уравнение на выбранные направления осей X и Y:

Учитывая, что 


Решив уравнения (2) получим:
При равномерном движении шарика по окружности его период вращения




Решение. 1. На тело в верхней точке действуют сила тяжести
сила натяжения Т стержня (рис.9). В результате действия двух сил тело движется по окружности, т.е. с центростремительным ускорением

где 


Направление сил Т1 и Р совпадает с вектором ац.с, поэтому второй закон Ньютона запишем в скалярном виде:



Выразим в СИ числовые значения R и g: R=0,125 м, g=9,81 м/с2.
Вычислим по формуле (5) искомую силу натяжения стержня в верхней точке траектории:

2. В нижней точке траектории на тело действуют (рис.10) те же силы 


После подстановки имеем
Пример 4. Маховик в виде диска массой m=50 кг и радиусом r=20 см, был раскручен до частоты n1=480 об/мин и затем предоставлен самому себе. Под воздействием трения маховик остановился.
Найти момент М сил трения, считая его постоянным, принимая, что: а) маховик остановился через t=50 c; б) маховик до полной остановки сделал N=200 об.
Решение. а). По второму закону динамики вращательного движения изменение момента импульса вращающегося тела равно произведению момента силы, действующего на тело, на время действия этого момента
где J – момент инерции маховика, 

Так как 

Момент инерции диска относительно его геометрической оси
Подставив выражение момента инерции в формулу (1), найдем:

Выразим угловую скорость маховика через частоту вращения

Подставим числовые значения в формулу (2), получим

б). В условии задачи дано число оборотов, сделанных маховиком до остановки, т.е. его угловое перемещение. Поэтому следует применить формулу, выражающую связь работы с изменением кинетической энергии:

так как
Работа при вращательном движении определяется по формуле:
Подставим это выражение работы, а также выражение момента инерции диска в формулу (3), получим:
Отсюда момент силы трения

Угол поворота в радианах

Подставим числовые значения в выражение (4), найдем

Знак «минус» показывает, что момент силы трения оказывает тормозящее действие.
Пример 5. Определить расстояние от центра Земли до искусственного спутника и скорость его относительно поверхности Земли, если спутник запущен так, что он движется в плоскости земного экватора и с Земли все время кажется неподвижным.
Решение. С достаточной степенью точности можно считать, что на спутник при его движении действует только сила земного притяжения:
где m – масса спутника; М – масса Земли; R – расстояние от центра Земли до спутника.
Под действием этой силы спутник, равномерно движется по окружности с ускорением 



Поскольку спутник с Земли все время кажется неподвижным, то 

Определим скорость движения спутника:
Пример 6. Сравнить ускорение свободного падения у поверхности Луны с ускорением свободного падения у поверхности Земли.
Решение. На тело массой m вблизи поверхности Земли и Луны будут действовать соответственно силы:
где 
Поскольку угловое перемещение φ, угловая скорость
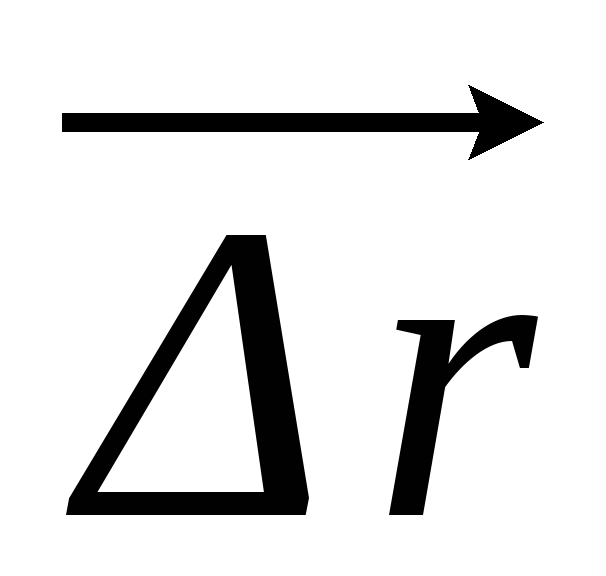


Если тело одновременно участвует в двух вращательных движениях с угловыми скоростями 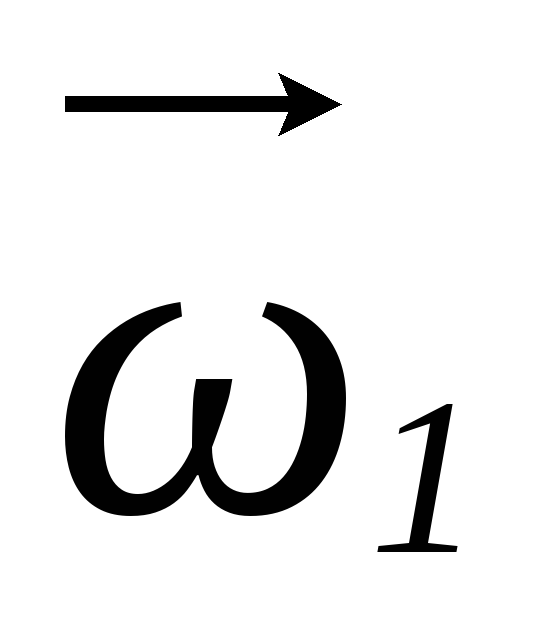
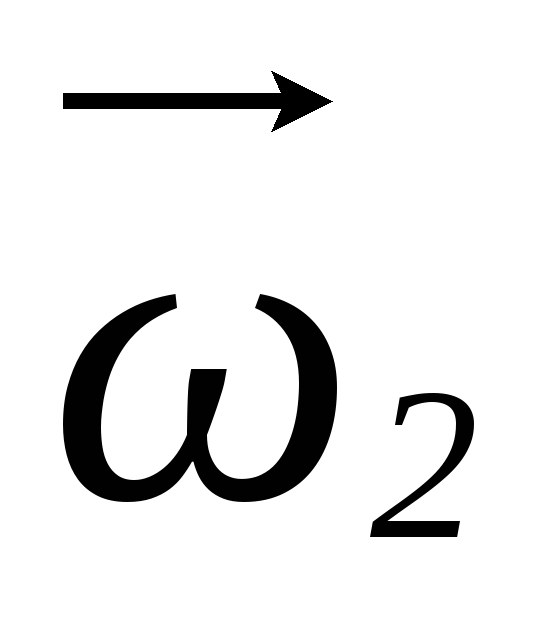

W=
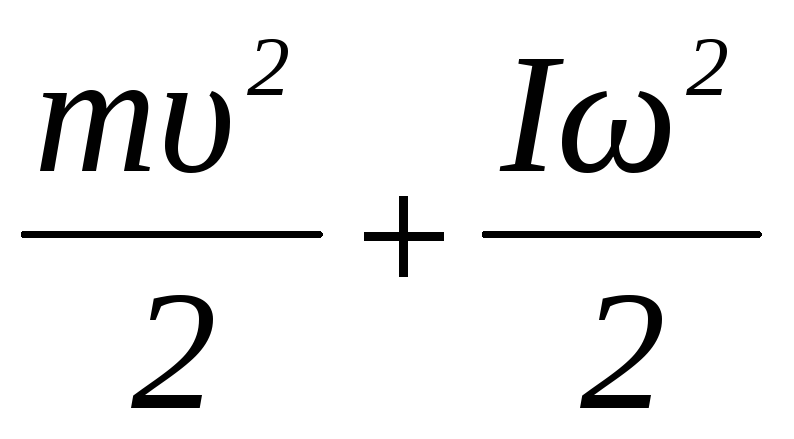
где – I– момент инерции тела относительно оси, проходящей через центр
тяжести параллельно образующей;

Момент инерции сплошного цилиндра относительно его оси равен
I = 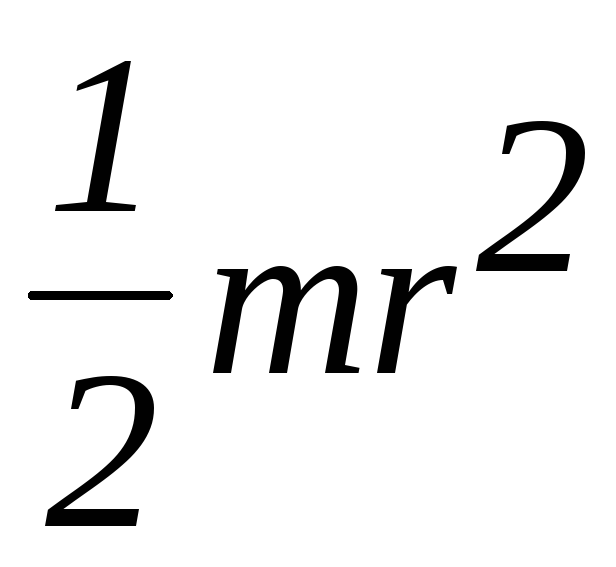
где r– радиус цилиндра.
Линейная скорость точек поверхности качения


Подставим I и 
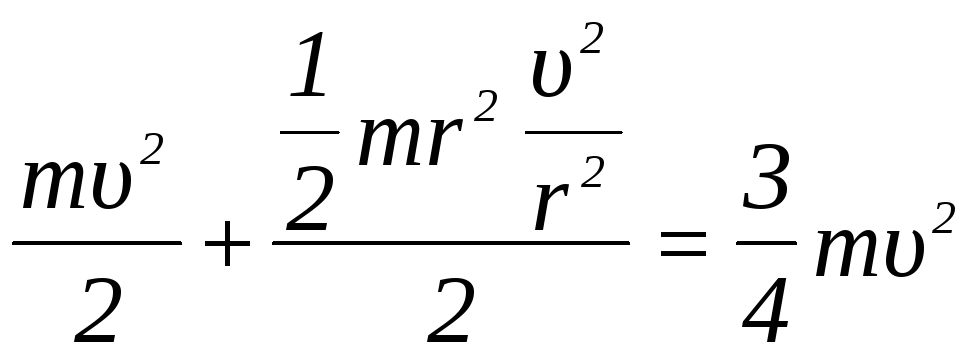
Кинетическая энергия цилиндра погашена работой силы торможения, то есть
F S = 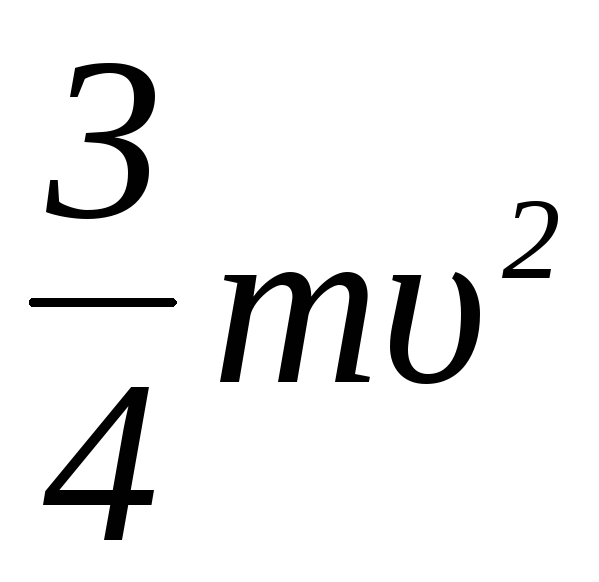
Искомая скорость 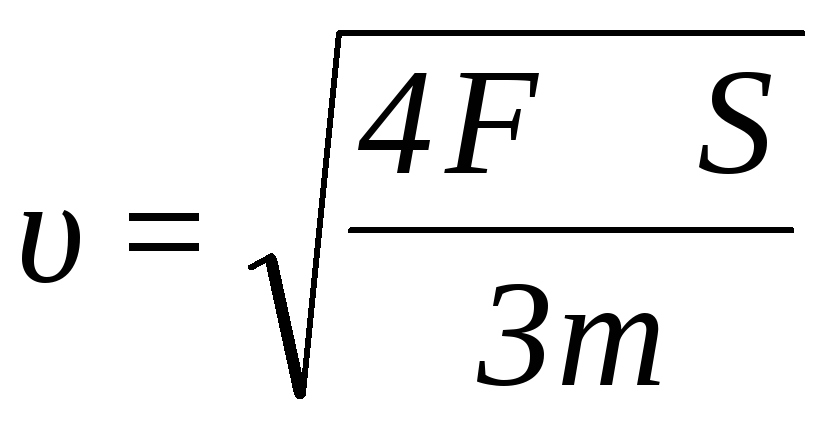
Вычисляем: 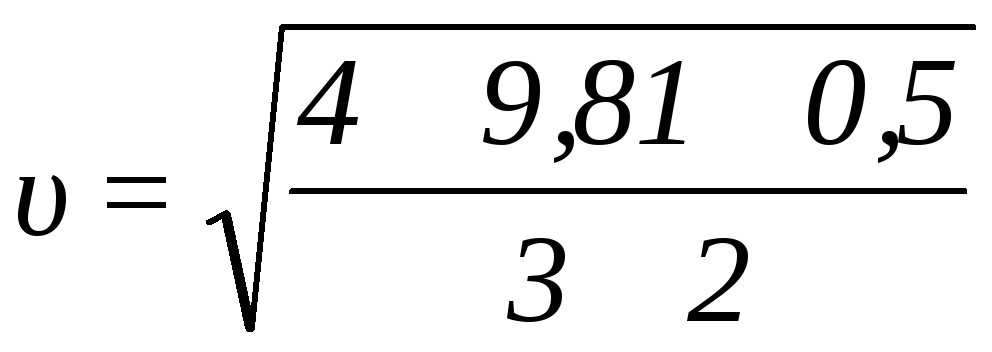
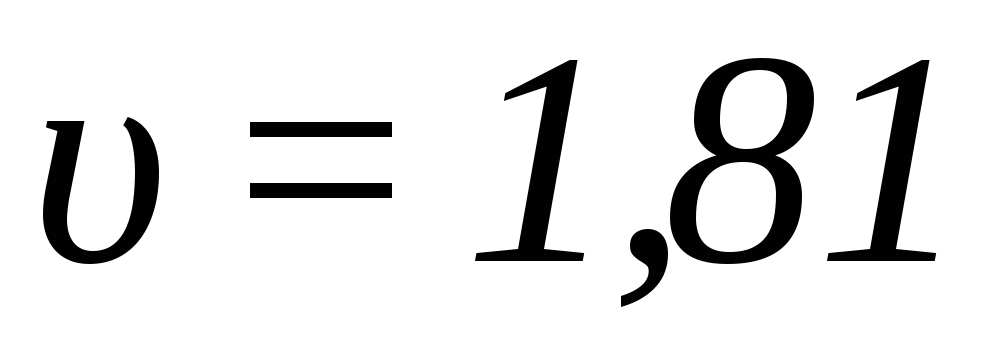
Пример 5. Две гири с массамиm1=2кг и m2=1кгсоединены нитью, перекинутой через блок массойm=1кг. Найти ускорениеа, с которым движутся гири, и силы натяженияТ1иТ2нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
Рисунок 6 – Пример 5
Запишем в векторной форме уравнения поступательного движения первой и второй гири
m1

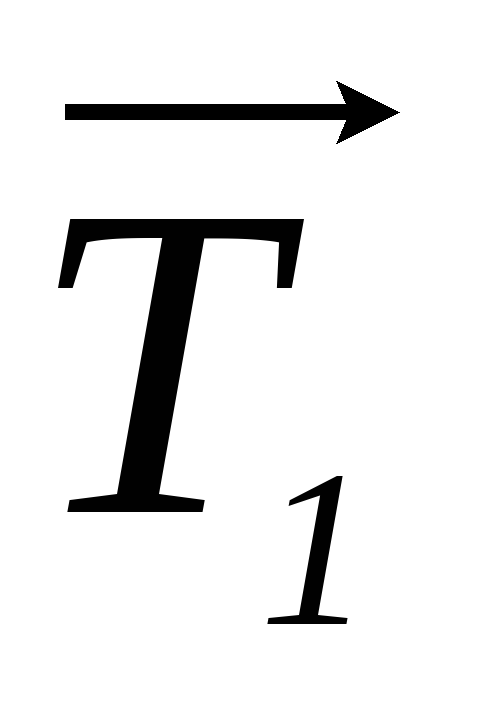

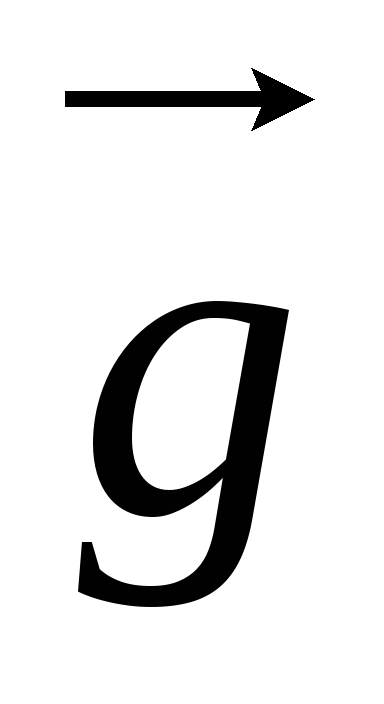
и уравнение вращательного движения диска
J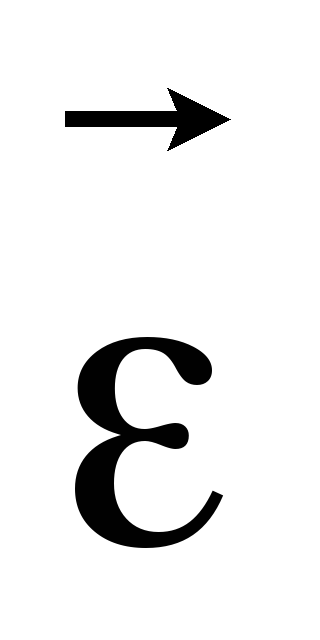
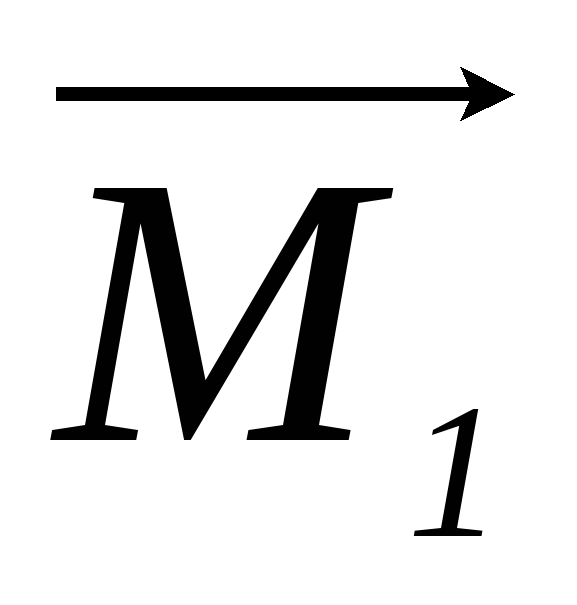

Спроектируем первые два уравнения на ось х, а последнее на ось yи добавим уравнение кинематической связи. Получим систему 4-х уравнений:
Подставим (23) в (22): J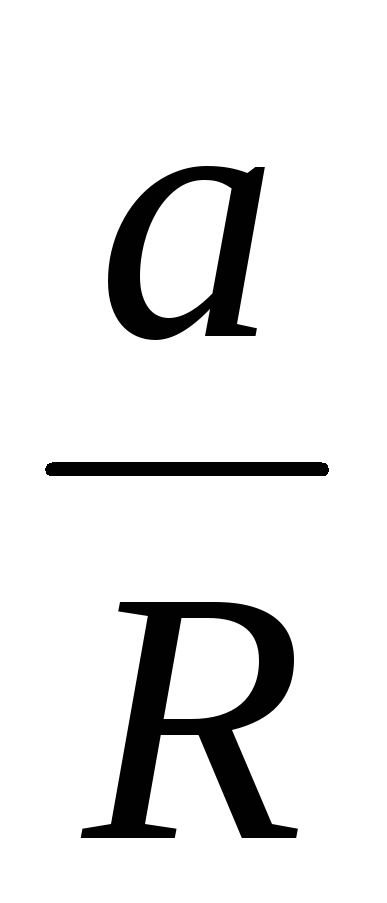
Вычтем (21) из (20), подставим в полученное выражение (24) и найдем
а =
Подставляя (25) в (20) и (21), получим
Пример 6. Блок массойm=1кгукреплен на конце стола. Гири1и2одинаковой массойm1 = m2 = 1 кгсоединены нитью, перекинутой через блок. Коэффициент трения гири2о столk =0,1.Найти ускорениеa, с которым движутся гири, и силы натяженияТ1 иТ2нитей. Блок считать однородным диском. Трением в блоке пренебречь.
Рисунок 7 –Пример 6
Запишем второй закон Ньютона в проекциях на ось х и у:
где 
(Т1-Т2)R=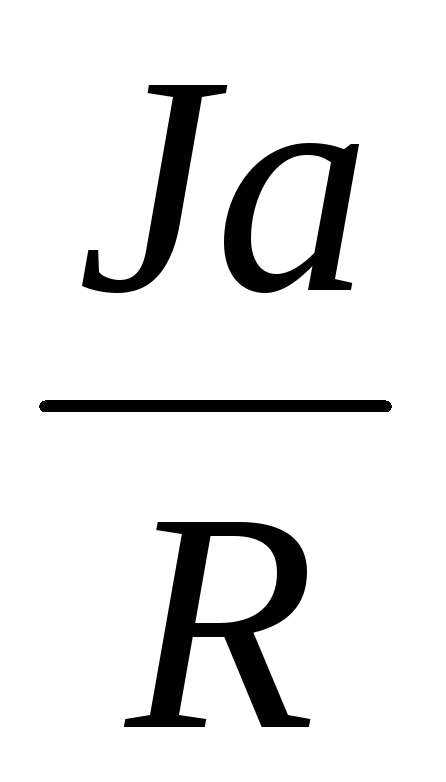
где J = 
откуда Т1-Т2 = 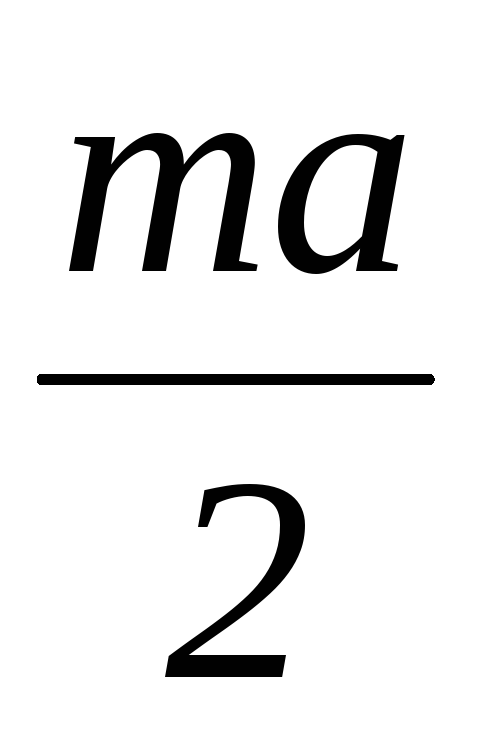
Из уравнений (26) – (28) найдем
Т1= 
Т2=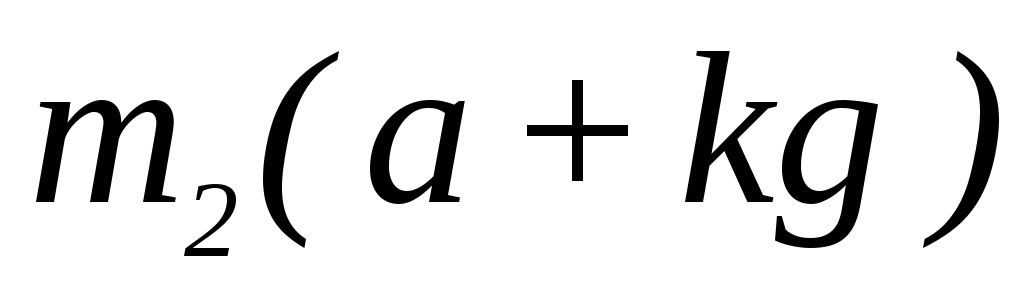
mg (1-k) = 

откуда а = 
Тогда из уравнения (30)
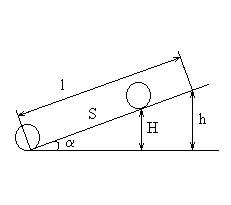
Пример 7. Мальчик катит обруч по горизонтальной дороге со скоростью =7,2 км/ч. На какое расстояниеSможет вкатиться обруч на горку за счет его кинетической энергии? Уклон горки равен10мна каждые100мпути.
Рисунок 8 – Пример 7
У основания горки обруч обладал кинетической энергией Wk, которая складывалась из кинетической энергии поступательного движения и кинетической энергии вращения. Когда обруч вкатился на горку на расстояниеS, его кинетическая энергия перешла в потенциальную.Wk = Wп.
Wk = 
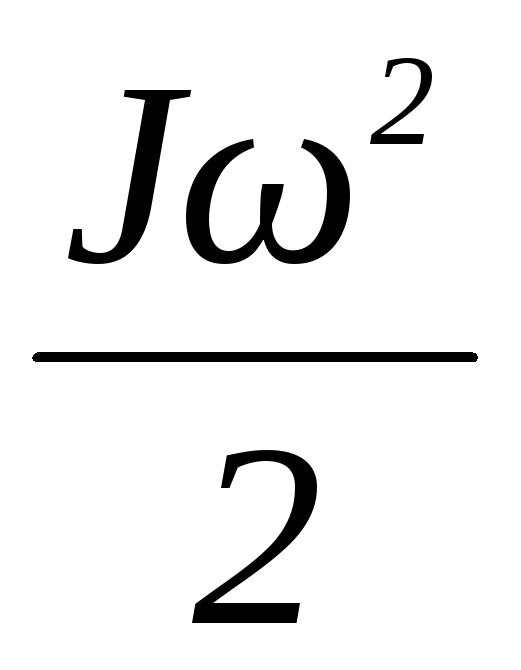
Момент инерции обруча J=mR 2 , частота вращения = 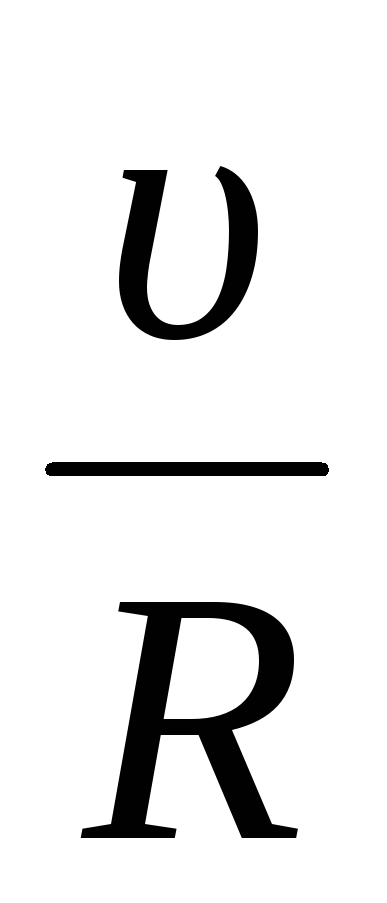
Тогда Wk = 

откуда Н = 
Из рисунка видно, что 
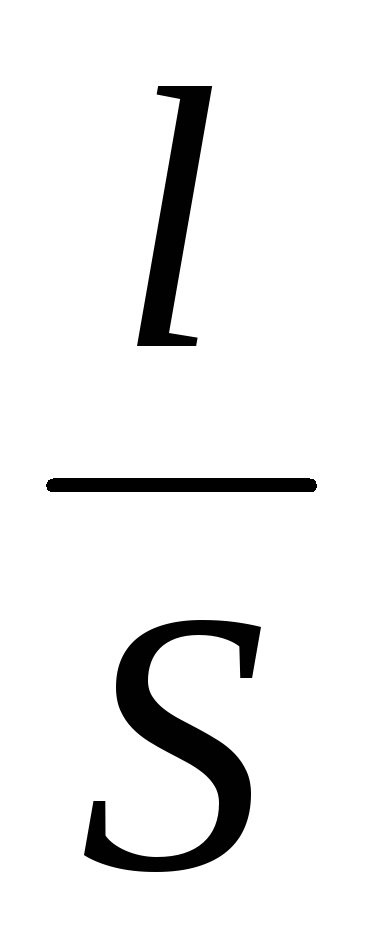
откуда S = 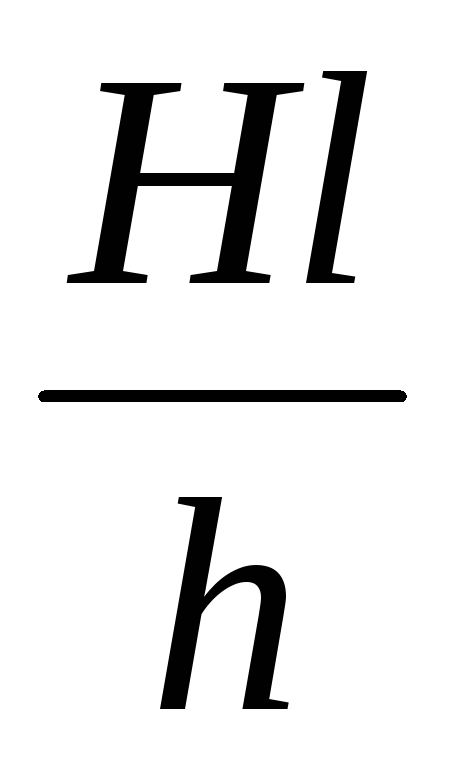
или S = 
Подставив числовые данные с учетом = 2 м/с, получимS = 4,1м.
При решении задач на динамику твердого тела, как правило, необходимо применять основное уравнение динамики вращательного движения. Часто в подобных задачах твердое тело приводится в движение силами натяжения нитей, к которым подвешены грузы, поэтому необходимо также записывать уравнения движения (второй закон Ньютона) для грузов. Условие, связывающее два типа движения, как правило, заключается в отсутствии проскальзывания нити, что позволяет получить кинематическую связь между линейным ускорением груза и угловым ускорением твердого тела. Рассмотрим конкретные примеры.
 |
Задача 1. Два тела, массы которых 
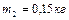
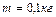
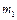
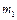
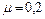
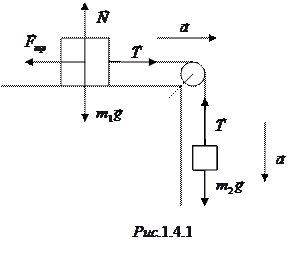
Применим для грузов второй закон Ньютона, а для блока – основное уравнение динамики вращательного движения. Силы, действующие на грузы, показаны на рис.1.4.1.
Для груза 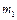
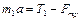

а по определению сила трения скольжения
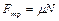
Для груза 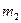
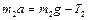
Наконец, уравнение вращательного движения блока
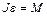
где 
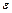

При отсутствии скольжения нити по блоку его угловое ускорение связано с линейным ускорением грузов по формуле 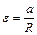
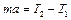
Исключая из (1.4.1) силы трения и реакции опоры, получаем
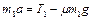
Наконец, складывая уравнения (1.4.2), (1.4.4), (1.4.5), получаем
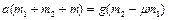
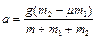
Подставляя числовые значения, получаем
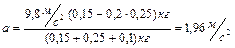
Подставляя (1.4.6) в (1.4.2) и (1.4.5), находим силы натяжения:
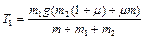
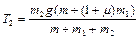
Вычисления приводят к результатам:

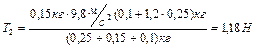
Задача 2. В однородном диске массой 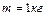

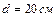
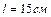
Данное тело можно представить как совокупность сплошного диска, изготовленного из материала с некоторой плотностью, и другого диска из материала с такой же по величине, но противоположной по знаку плотностью, расположенного в отверстии первого диска. Тогда результирующий момент инерции этой системы можно найти, вычитая из момента инерции первого диска момент инерции второго диска.
Для первого диска

а для второго по теореме Штейнера
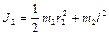
где 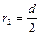
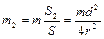
Тогда 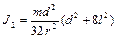
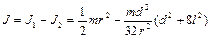
Выполняя вычисления, находим
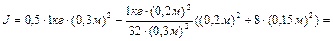
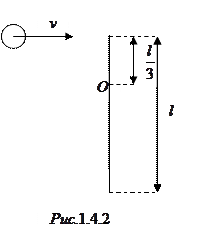 |
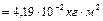
Задача 3. Однородный тонкий стержень массой 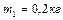
длиной 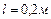
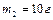

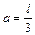
Для определения угловой скорости вращения стержня воспользуемся законом сохранения момента импульса. Рассматривая шарик как материальную точку, получаем:
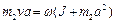
где момент инерции стержня относительно точки О по теореме Штейнера равен

Из (1.4.7) и (1.4.8) находим угловую скорость стержня сразу после удара
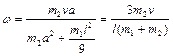
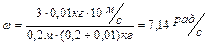
Для определения линейной скорости нижнего конца стержня воспользуемся связью линейной и угловой скорости: 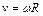
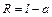
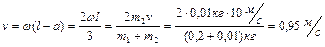
 |
Задача 4. На ступенчатый цилиндрический блок намотаны в противоположных направлениях две нити с подвешенными к ним грузами массами 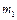

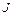
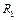
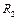
Запишем второй закон Ньютона для грузов в проекции на вертикальное направление
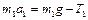

где 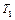
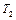
Уравнение вращательного движения блока
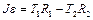
В силу отсутствия проскальзывания нитей по блоку можно записать

Из (1.4.9) – (1.4.11) следует
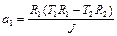
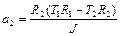
Подставляя в уравнения движения грузов, получаем систему уравнений для определения сил натяжения нитей


Решая систему (1.4.13), находим
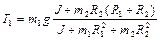
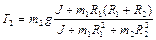
Подстановка полученных результатов в (1.4.12) дает
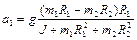
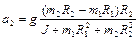
Задача 5. Два диска с моментами инерции 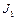

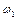
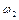
Применим закон сохранения момента импульса. Получаем

где 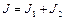

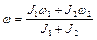
Для определения количества теплоты, выделившегося в результате взаимодействия дисков, воспользуемся законом сохранения энергии, согласно которому
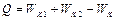
где 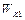
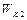
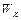
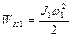
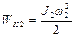
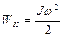
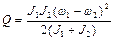
Задача 6. Тонкий обруч радиуса 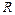
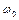
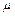
Так как действующая на обруч сила трения постоянна, то вращение обруча будет равнозамедленным, и мы можем применить уравнения равнозамедленного вращения
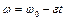
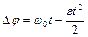
Если обруч сделает до остановки 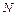
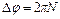

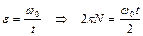
Воспользуемся законом сохранения энергии, согласно которому работа силы трения равна изменению кинетической энергии обруча

Здесь 
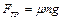
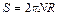
Решая систему уравнений (1.4.14), (1.4.15) с учетом выписанных соотношений для пути, силы трения и момента инерции, получаем
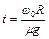
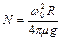
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8832 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
“>