Галочка вниз в информатике

Каждого, кто начинает изучать информатику, учат двоичной системе исчисления. Именно она используется для вычисления логических операций. Рассмотрим ниже все самые элементарные логические операции в информатике. Ведь если задуматься, именно они используются при создании логики вычислительных машин и приборов.

Отрицание

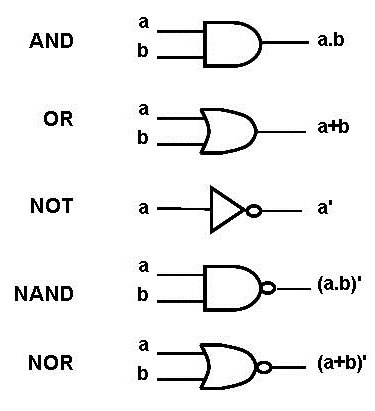
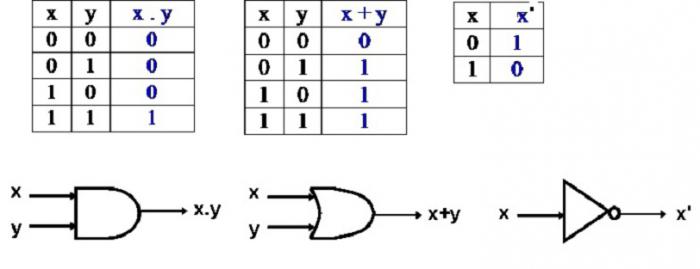
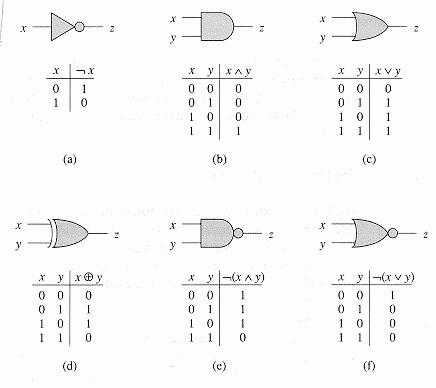
Перед тем как начать подробно рассматривать конкретные примеры, перечислим основные логические операции в информатике:

Также перед началом изучения логических операций стоит сказать, что в информатике ложь обозначается "0", а правда "1".

Для каждого действия, как и в обычной математике, используются следующие знаки логических операций в информатике: ¬, v, &, ->.

Каждое действие возможно описать либо цифрами 1/0, либо просто логическими выражениями. Начнём рассмотрение математической логики с простейшей операции, использующей всего одну переменную.

Логическое отрицание – операция инверсии. Суть заключается в том, что если исходное выражение – истина, то результат инверсии – ложь. И наоборот, если исходное выражение – ложь, то результатом инверсии станет – правда.

При записи этого выражения используется следующее обозначение "¬A".

Приведём таблицу истинности – схему, которая показывает все возможные результаты операции при любых исходных данных.

Таблица истинности для инверсии

А	х	о
¬A	о	х

То есть, если у нас исходное выражение – истина (1), то его отрицание будет ложным (0). А если исходное выражение – ложь (0), то его отрицание – истина (1).

Сложение

Оставшиеся операции требуют наличия двух переменных. Обозначим одно выражение –

1. Е=1, Н=1 ,тогда Е v Н = 1. Если оба выражения истинны, тогда и их дизъюнкция также истинна.
2. Е=0, Н=1 ,в итоге Е v Н = 1. Е=1, Н=0 , тогда Е v Н= 1. Если хотябы одно из выражений истинно, тогда и результат их сложения будет истиной.
3. Е=0, Н=0 ,результат Е v Н = 0. Если оба выражения ложны, то их сумма также – ложь.

Для краткости создадим таблицу истинности.

Дизъюнкция

Е	х	х	о	о
Н	х	о	х	о
Е v Н	х	х	х	о

Умножение

Разобравшись с операцией сложения, переходим к умножению (конъюнкции). Воспользуемся теми же обозначениями, которые были приведены выше для сложения. При письме логическое умножение обозначается значком "&", либо буквой "И".

1. Е=1, Н=1 ,тогда Е & Н = 1. Если оба выражения истинны, тогда их конъюнкция – истина.
2. Если хотя бы одно из выражений – ложь, тогда результатом логического умножения также будет ложь.

• Е=1, Н=0, поэтому Е & Н = 0.
• Е=0, Н=1, тогда Е & Н = 0.
• Е=0, Н=0, итог Е & Н = 0.

Конъюнкция

Е	х	х
Н	х		х
Е & Н	х

Следствие

Логическая операция следования (импликация) – одна из простейших в математической логике. Она основана на единственной аксиоме – из правды не может следовать ложь.

1. Е=1, Н=, поэтому Е -> Н = 1. Если пара влюблена, то они могут целоваться – правда.
2. Е=0, Н=1, тогда Е -> Н = 1. Если пара не влюблена, то они могут целоваться – также может быть истиной.
3. Е=0, Н=0, из этого Е -> Н = 1. Если пара не влюблена, то они и не целуются – тоже правда.
4. Е=1, Н=0, результатом будет Е -> Н = 0. Если пара влюблена, то они не целуются – ложь.

Для облегчения выполнения математических действий также приведём таблицу истинности.

Импликация

Е	х	х	о	о
Н	х	о	х
Е -> Н	х	о	х	х

Равенство

Последней рассмотренной операцией станет логическое тождественное равенство или эквивалентность. В тексте оно может обозначаться как ". тогда и только тогда, когда. ". Исходя из этой формулировки, напишем примеры для всех исходных вариантов.

1. А=1, В=1, тогда А≡В = 1. Человек пьёт таблетки тогда и только тогда, когда болеет. (истина)
2. А=0, В=0, в итоге А≡В = 1. Человек не пьёт таблетки тогда и только тогда, когда не болеет. (истина)
3. А=1, В=0, поэтому А≡В = 0. Человек пьёт таблетки тогда и только тогда, когда не болеет. (ложь)
4. А=0, В=1 ,тогда А≡В = 0. Человек не пьёт таблетки тогда и только тогда, когда болеет. (ложь)

Эквивалентность

А	х	о	х	о
В	х	о		х
А≡В	х	х	о	о

Свойства

Итак, рассмотрев простейшие логические операции в информатике, можем приступить к изучению некоторых их свойств. Как и в математике, у логических операций существует свой порядок обработки. В больших логических выражениях операции в скобках выполняются в первую очередь. После них первым делом подсчитываем все значения отрицания в примере. Следующим шагом станет вычисление конъюнкции, а затем дизъюнкции. Только после этого выполняем операцию следствия и, наконец, эквивалентности. Рассмотрим небольшой пример для наглядности.

Порядок выполнения действий следующий.

Для того чтобы решить этот пример, нам потребуется построить расширенную таблицу истинности. При её создании помните, что столбцы лучше располагать в том же порядке, в каком и будут выполняться действия.

Решение примера

А

В

х о х о х х х х х о о х х х о о х о о х о о х о о о х о

Как мы видим, результатом решения примера станет последний столбец. Таблица истинности помогла решить задачу с любыми возможными исходными данными.

Заключение

В этой статье были рассмотрены некоторые понятия математической логики, такие как информатика, свойства логических операций, а также – что такое логические операции сами по себе. Были приведены некоторые простейшие примеры для решения задач по математической логике и таблицы истинности, необходимые для упрощения этого процесса.

Обозначения в логических операциях

Обозначения для логических связок:

отрицание (инверсия, логическое НЕ) обозначается ¬ (например, ¬А);

конъюнкция (логическое умножение, логическое И) обозначается /

дизъюнкция (логическое сложение, логическое ИЛИ) обозначается /

следование (импликация) обозначается → (например, А → В);

тождество обозначается ≡ (например, A ≡ B). Выражение A ≡ B истинно тогда и только тогда, когда значения A и B совпадают (либо они оба истинны, либо они оба ложны);

символ 1 (единица) используется для обозначения истины (истинного высказывания);

символ 0 (ноль) используется для обозначения лжи (ложного высказывания).

Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А → В и (¬А) / В равносильны, а А / В и А / В – нет (значения выражений разные, например, при А = 1, В = 0).

Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество. Таким образом, ¬А / В / С / D означает то же, что и

Возможна запись А / В / С вместо (А / В) / С. То же относится и к конъюнкции: возможна запись А / В / С вместо (А / В) / С.

Свойства логических операций

Общие свойства логических операций

Для набора из n логических переменных существует ровно 2n различных значений. Таблица истинности для логического выражения от n переменных содержит n+1 столбец и 2n строк.

Дизъюнкция

Если хоть одно из подвыражений, к которым применяется дизъюнкция, истинно на некотором наборе значений переменных, то и вся дизъюнкция истинна для этого набора значений.

Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже истинна.

Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже ложна.

Значение дизъюнкции не зависит от порядка записи подвыражений, к которым она применяется.

Конъюнкция

Если хоть одно из подвыражений, к которым применяется конъюнкция, ложно на некотором наборе значений переменных, то и вся конъюнкция ложна для этого набора значений.

Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то конъюнкция этих выражений тоже истинна.

Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то конъюнкция этих выражений тоже ложна.

Значение конъюнкции не зависит от порядка записи подвыражений, к которым она применяется.

Простые дизъюнкции и конъюнкции

Назовем (для удобства) конъюнкцию простой, если подвыражения, к которым применяется конъюнкция, – различные переменные или их отрицания. Аналогично, дизъюнкция называется простой, если подвыражения, к которым применяется дизъюнкция, – различные переменные или их отрицания.

Простая конъюнкция принимает значение 1 (истина) ровно на одном наборе значений переменных.

Простая дизъюнкция принимает значение (ложь) ровно на одном наборе значений переменных.

Импликация

Импликация A →B равносильна дизъюнкции (¬А) / В. Эту дизъюнкцию можно записать и так: ¬А / В.

Импликация A →B принимает значение 0 (ложь) только если A=1 и B=0. Если A=0, то импликация A →B истинна при любом значении B.

НЕКОТОРЫЕ

СВОЙСТВА ЛОГИЧЕСКИХ ОПЕРАЦИЙ

1. Обозначения

1.1. Обозначения для логических связок (операций):

a) отрицание (инверсия, логическое НЕ) обозначается ¬ (например, ¬А);

b) конъюнкция (логическое умножение, логическое И) обозначается /
(например, А / В) либо & (например, А & В);

c) дизъюнкция (логическое сложение, логическое ИЛИ) обозначается /
(например, А / В);

d) следование (импликация) обозначается → (например, А → В);

e) тождество обозначается ≡ (например, A ≡ B). Выражение A ≡ B истинно тогда и только тогда, когда значения A и B совпадают (либо они оба истинны, либо они оба ложны);

f) символ 1 используется для обозначения истины (истинного высказывания); символ 0 – для обозначения лжи (ложного высказывания).

1.2. Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А → В и (¬А) / В равносильны, а А / В и А / В – нет (значения выражений разные, например, при А = 1, В = 0).

1.3. Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество. Таким образом, ¬А / В / С / D означает то же, что и

Возможна запись А / В / С вместо (А / В) / С. То же относится и к конъюнкции: возможна запись А / В / С вместо (А / В) / С.

2. Свойства

Приведенный ниже список НЕ претендует на полноту, но, надеемся, достаточно представителен.

2.1. Общие свойства

1. Для набора из n логических переменных существует ровно 2n различных значений. Таблица истинности для логического выражения от n переменных содержит n+1 столбец и 2n строк.

2.2.Дизъюнкция

1. Если хоть одно из подвыражений, к которым применяется дизъюнкция, истинно на некотором наборе значений переменных, то и вся дизъюнкция истинна для этого набора значений.
2. Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже истинна.
3. Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже ложна.
4. Значение дизъюнкции не зависит от порядка записи подвыражений, к которым она применяется.

2.3. Конъюнкция

1. Если хоть одно из подвыражений, к которым применяется конъюнкция, ложно на некотором наборе значений переменных, то и вся конъюнкция ложна для этого набора значений.
2. Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то конъюнкция этих выражений тоже истинна.
3. Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то конъюнкция этих выражений тоже ложна.
4. Значение конюнкции не зависит от порядка записи подвыражений, к которым она применяется.

2.4. Простые дизъюнкции и конъюнкции

Назовем (для удобства) конъюнкцию простой, если подвыражения, к которым применяется конъюнкция, – различные переменные или их отрицания. Аналогично, дизъюнкция называется простой, если подвыражения, к которым применяется дизъюнкция, – различные переменные или их отрицания.

1. Простая конъюнкция принимает значение 1 (истина) ровно на одном наборе значений переменных.
2. Простая дизъюнкция принимает значение 0 (ложь) ровно на одном наборе значений переменных.

2.5. Импликация

1. Импликация A →B равносильна дизъюнкции (¬А) / В. Эту дизъюнкцию можно записать и так: ¬А / В.
2. Импликация A →B принимает значение 0 (ложь) только если A=1 и B=0. Если A=0, то импликация A →B истинна при любом значении B.