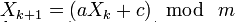Содержание
- 1 Генератор псевдослучайных чисел и генератор случайных чисел
- 2 Придумываем свой алгоритм ГПСЧ
- 3 Линейный конгруэнтный ГПСЧ
- 4 Как устроен Math.random()
- 5 Предсказываем Math.random()
- 5.0.1 Введение
- 5.0.2 Как отличить случайную последовательность чисел от неслучайной?
- 5.0.3 Чуть более сложный пример или число Пи
- 5.0.4 Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)
- 5.0.5 Уязвимости ГПСЧ
- 5.0.6 Линейный конгруэнтный ГПСЧ(LCPRNG)
- 5.0.7 Предсказание результатов линейно-конгруэнтного метода
- 5.0.8 Взлом встроенного генератора случайных чисел в Java
- 5.0.9 Взлом ГПСЧ Mersenne twister в PHP
- 5.0.10 Область для взлома
- 5.0.11 Задание распределения для генератора псевдослучайных чисел
- 5.0.12 Экспоненциальное распределение
- 5.0.13 Тесты ГПСЧ
- 6 Алгоритм Лемера
- 7 Алгоритм Вичмана-Хилла
- 8 Линейный конгруэнтный алгоритм
- 9 Алгоритм Фибоначчи с запаздываниями
- 10 Заключение
Вы когда-нибудь задумывались, как работает Math.random()? Что такое случайное число и как оно получается? А представьте вопрос на собеседовании?—?напишите свой генератор случайных чисел в пару строк кода. И так, что же это такое, случайность и возможно ли ее предсказать?
Меня очень увлекают различные IT головоломки и задачки и генератор случайных чисел — одна из таких задачек. Обычно в своем телеграм канале я разбираю всякие головоломки и разные задачи с собеседований. Задача про генератор случайных чисел набрала большую популярность и мне захотелось увековечить ее в недрах одного из авторитетных источников информации — то бишь здесь, на Хабре.
Данный материал будет полезен всем тем фронтендерам и Node.js разработчикам, кто на острие технологий и хочет попасть в блокчейн проект/стартап, где вопросы про безопасность и криптографию, хотя бы на базовом уровне, спрашивают даже у фронтендеров.
Генератор псевдослучайных чисел и генератор случайных чисел
Для того, чтобы получить что-то случайное, нам нужен источник энтропии, источник некого хаоса из который мы будем использовать для генерации случайности.
Этот источник используется для накопления энтропии с последующим получением из неё начального значения (initial value, seed), которое необходимо генераторам случайных чисел (ГСЧ) для формирования случайных чисел.
Генератор ПсевдоСлучайных Чисел использует единственное начальное значение, откуда и следует его псевдослучайность, в то время как Генератор Случайных Чисел всегда формирует случайное число, имея в начале высококачественную случайную величину, которая берется из различных источников энтропии.
Энтропия?—?это мера беспорядка. Информационная энтропия?—?мера неопределённости или непредсказуемости информации.
Выходит, что чтобы создать псевдослучайную последовательность нам нужен алгоритм, который будет генерить некоторую последовательность на основании определенной формулы. Но такую последовательность можно будет предсказать. Тем не менее, давайте пофантазируем, как бы могли написать свой генератор случайных чисел, если бы у нас не было Math.random()
ГПСЧ имеет некоторый алгоритм, который можно воспроизвести.
ГСЧ?—?это получение чисел полностью из какого либо шума, возможность просчитать который стремится к нулю. При этом в ГСЧ есть определенные алгоритмы для выравнивания распределения.
Придумываем свой алгоритм ГПСЧ
Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG)?—?алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).
Мы можем взять последовательность каких-то чисел и брать от них модуль числа. Самый простой пример, который приходит в голову. Нам нужно подумать, какую последовательность взять и модуль от чего. Если просто в лоб от 0 до N и модуль 2, то получится генератор 1 и 0:
Эта функция генерит нам последовательность 01010101010101… и назвать ее даже псевдослучайной никак нельзя. Чтобы генератор был случайным, он должен проходить тест на следующий бит. Но у нас не стоит такой задачи. Тем не менее даже без всяких тестов мы можем предсказать следующую последовательность, значит такой алгоритм в лоб не подходит, но мы в нужном направлении.
А что если взять какую-то известную, но нелинейную последовательность, например число PI. А в качестве значения для модуля будем брать не 2, а что-то другое. Можно даже подумать на тему меняющегося значения модуля. Последовательность цифр в числе Pi считается случайной. Генератор может работать, используя числа Пи, начиная с какой-то неизвестной точки. Пример такого алгоритма, с последовательностью на базе PI и с изменяемым модулем:
Но в JS число PI можно вывести только до 48 знака и не более. Поэтому предсказать такую последовательность все так же легко и каждый запуск такого генератора будет выдавать всегда одни и те же числа. Но наш генератор уже стал показывать числа от 0 до 9.
Мы получили генератор чисел от 0 до 9, но распределение очень неравномерное и каждый раз он будет генерировать одну и ту же последовательность.
Мы можем взять не число Pi, а время в числовом представлении и это число рассматривать как последовательность цифр, причем для того, чтобы каждый раз последовательность не повторялась, мы будем считывать ее с конца. Итого наш алгоритм нашего ГПСЧ будет выглядеть так:
Вот это уже похоже на генератор псевдослучайных чисел. И тот же Math.random()?—?это ГПСЧ, про него мы поговорим чуть позже. При этом у нас каждый раз первое число получается разным.
Собственно на этих простых примерах можно понять как работают более сложные генераторы случайных числе. И есть даже готовые алгоритмы. Для примера разберем один из них?—?это Линейный конгруэнтный ГПСЧ(LCPRNG).
Линейный конгруэнтный ГПСЧ
Линейный конгруэнтный ГПСЧ(LCPRNG)?—?это распространённый метод для генерации псевдослучайных чисел. Он не обладает криптографической стойкостью. Этот метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой формулой. Получаемая последовательность зависит от выбора стартового числа?—?т.е. seed. При разных значениях seed получаются различные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:
Многие языки программирования используют LСPRNG (но не именно такой алгоритм(!)).
Как говорилось выше, такую последовательность можно предсказать. Так зачем нам ГПСЧ? Если говорить про безопасность, то ГПСЧ?—?это проблема. Если говорить про другие задачи, то эти свойства?—?могут сыграть в плюс. Например для различных спец эффектов и анимаций графики может понадобиться частый вызов random. И вот тут важны распределение значений и перформанс! Секурные алгоритмы не могут похвастать скоростью работы.
Еще одно свойство?—?воспроизводимость. Некоторые реализации позволяют задать seed, и это очень полезно, если последовательность должна повторяться. Воспроизведение нужно в тестах, например. И еще много других вещей существует, для которых не нужен безопасный ГСЧ.
Как устроен Math.random()
Метод Math.random() возвращает псевдослучайное число с плавающей запятой из диапазона [0, 1), то есть, от 0 (включительно) до 1 (но не включая 1), которое затем можно отмасштабировать до нужного диапазона. Реализация сама выбирает начальное зерно для алгоритма генерации случайных чисел; оно не может быть выбрано или сброшено пользователем.
Как устроен алгоритм Math.random()?—?интересный вопрос. До недавнего времени, а именно до 49 Chrome использовался алгоритм MWC1616:
Именно этот алгоритм генерит нам последовательность псевдослучайных чисел в промежутке между 0 и 1.
Предсказываем Math.random()
Чем это было чревато? Есть такой квест: alf.nu/ReturnTrue
В нем есть задача:
Что нужно вписать вместо вопросов, чтобы функция вернула true? Кажется что это невозможно. Но, это возможно, если вы заглядывали в спеку и видели алгоритм ГПСЧ V8. Решение этой задачи в свое время мне показал Роман Дворнов:
Этот код работал в 70% случаев для Chrome
Введение
Генераторы случайных чисел — ключевая часть веб-безопасности. Небольшой список применений:
- Генераторы сессий(PHPSESSID)
- Генерация текста для капчи
- Шифрование
- Генерация соли для хранения паролей в необратимом виде
- Генератор паролей
- Порядок раздачи карт в интернет казино
Как отличить случайную последовательность чисел от неслучайной?
Пусть есть последовательность чисел: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 . Является ли она случайной? Есть строгое определение для случайной величины. Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать. Но оно не помогает ответить на наш вопрос, так как нам не хватает информации для ответа. Теперь скажем, что данные числа получились набором одной из верхних строк клавиатуры. «Конечно не случайная» — воскликните Вы и тут же назовете следующие число и будете абсолютно правы. Последовательность будет случайной только если между символами, нету зависимости. Например, если бы данные символы появились в результате вытягивания бочонков в лото, то последовательность была бы случайной.
Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.
Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)
Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.
Уязвимости ГПСЧ
- Предсказуемая зависимость между числами.
- Предсказуемое начальное значение генератора.
- Малая длина периода генерируемой последовательности случайных чисел, после которой генератор зацикливается.
Линейный конгруэнтный ГПСЧ(LCPRNG)
Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:
где a(multiplier), c(addend), m(mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.
Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].
Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений
Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.
Предсказание результатов линейно-конгруэнтного метода
Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.
Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.
Взлом встроенного генератора случайных чисел в Java
Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код(jdk1.7) данного класса можно увидеть используемые константы
Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)
Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).
Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:
до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так
Вывод данной программы будет примерно таким:
Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.
И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));
И всё, мы успешно взломали ГПСЧ в Java.
Взлом ГПСЧ Mersenne twister в PHP
Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.
Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:
10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor
Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так
Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.
Область для взлома
Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed’а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.
Задание распределения для генератора псевдослучайных чисел
Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.
Треугольное распределение
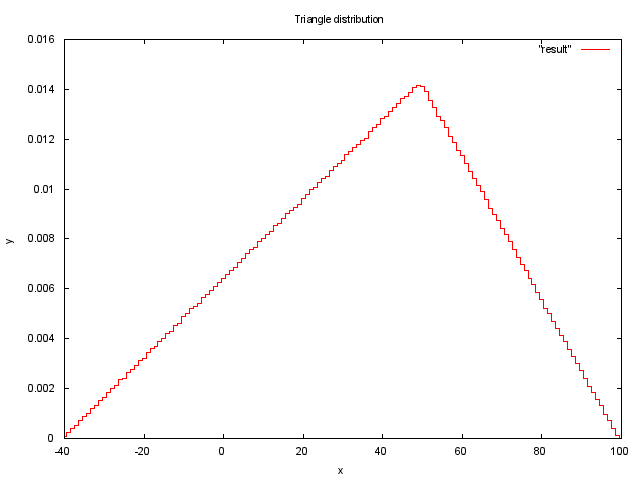
Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.
В данном случае мы берем случайную величину rand() и задаем ей распределение, исходя из функции треугольного распределения. Для параметров a = -40, b = 100, c = 50 график 10000000 измерений будет выглядеть так
Экспоненциальное распределение
Пусть требуется получить датчик экспоненциально распределенных случайных величин. В этом случае F(x) = 1 – exp(-lambda * x). Тогда из решения уравнения y = 1 – exp(-lambda * x) получаем x = -log(1-y)/lambda.
Можно заметить, что выражение под знаком логарифма в последней формуле имеет равномерное распределение на отрезке [0,1), что позволяет получать другую, но так же распределённую последовательность по формуле: x = -log(y)/lambda, где y есть случайная величина(rand()).
Тесты ГПСЧ
Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.
Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.
В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.

В этой статье я покажу, как генерировать случайные числа с помощью четырех разных алгоритмов: алгоритма Лемера (Lehmer), линейного конгруэнтного алгоритма ( linear congruential algorithm), алгоритма Вичмана-Хилла (Wichmann-Hill) и алгоритма Фибоначчи с запаздываниями (lagged Fibonacci algorithm).
Но зачем обременять себя созданием собственного генератора случайных чисел (random number generator, RNG), когда в Microsoft .NET Framework уже есть эффективный и простой в использовании класс Random? Существует два сценария, где вам может понадобиться создать свой RNG. Во-первых, в разные языки программирования встроены разные алгоритмы генерации случайных чисел, а значит, если вы пишете код, который будет переноситься на несколько языков, можно создать собственный RNG, чтобы реализовать его во всех нужных вам языках. Во-вторых, некоторые языки, в частности R, имеют лишь глобальный RNG, поэтому, если вы захотите создать несколько генераторов, вам придется писать свой RNG.
Хороший способ получить представление о том, куда я клоню в этой статье, — взглянуть на демонстрационную программу на рис. 1. Демонстрационная программа начинает с создания очень простого RNGЮ используя алгоритм Лемера. Затем с помощью RNG генерируется 1000 случайных целых чисел между 0 и 9 включительно. За кулисами записываются счетчики для каждого из сгенерированных целых чисел, которые потом отображаются на экране. Этот процесс повторяется для линейного конгруэнтного алгоритма, алгоритма Вичмана-Хилла и алгоритм Фибоначчи с запаздываниями.
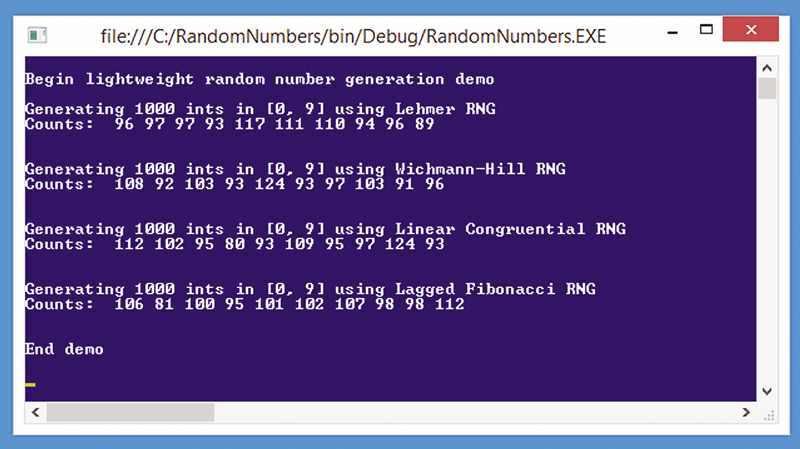
Рис. 1. Демонстрация упрощенной генерации случайных чисел
В этой статье предполагается, что вы умеете программировать хотя бы на среднем уровне, но ничего не знаете о генерации случайных чисел. Демонстрационная программа написана на C#, но, поскольку один из основных случаев использования собственной генерации случайных чисел — написание портируемого кода, эта программа разработана так, чтобы ее можно было легко транслировать на другие языки.
Алгоритм Лемера
Самый простой приемлемый метод генерации случайных чисел — алгоритм Лемера. (Для простоты я использую термин «генерация случайных чисел» вместо более точного термина «генерация псевдослучайных чисел».) Выраженный в символьном виде, алгоритм Лемера представляет собой следующее:
На словах это звучит так: «новое случайное число является старым случайным числом, умножаемым на константу a, после чего над результатом выполняется операция по модулю константы m». Например, предположим, что в некий момент текущее случайное число равно 104, a = 3 и m = 100. Тогда новое случайное число будет равно 3 * 104 mod 100 = 312 mod 100 = 12. Вроде бы просто, но в реализации этого алгоритма много хитроумных деталей.
Чтобы создать демонстрационную программу, я запустил Visual Studio, выбрал шаблон C# Console Application и назвал проект RandomNumbers. В этой программе нет значимых зависимостей от .NET Framework, поэтому подойдет любая версия Visual Studio.
После загрузки кода шаблона в окно редактора я переименовал в окне Solution Explorer файл Program.cs в более описательный RandomNumbersProgram.cs, и Visual Studio автоматически переименовала класс Program за меня. В начале кода я удалил все лишние выражения using, оставив только ссылки на пространства имен верхнего уровня System и Collections.Generic.
Затем я добавил класс с именем LehmerRng для реализации RNG-алгоритма Лемера. Код показан на рис. 2. Версия алгоритма Лемера за 1988 год использует a = 16807 и m = 2147483647 (которое является int.MaxValue). Позднее, в 1993 году Лемер предложил другую версию, где a = 48271 как чуть более качественную альтернативу. Эти значения берутся из математической теории. Демонстрационный код основан на знаменитой статье С. К. Парка (S. K. Park) и К. У. Миллера (K. W. Miller) «Random Number Generators: Good Ones Are Hard to Find».
Рис. 2. Реализация алгоритма Лемера
Проблема реализации в том, чтобы предотвращать арифметическое переполнение. Алгоритм Лемера использует ловкий алгебраический трюк. Значение q является результатом m / a (целочисленное деление), а значение r равно m % a (m по модулю a).
При инициализации RNG Лемера начальным (зародышевым) значением можно использовать любое целое число в диапазоне [1, int.MaxValue – 1]. Многие RNG имеют конструктор без параметров, который получает системные дату и время, преобразует их в целое число и использует в качестве начального значения.
RNG Лемера вызывается в методе Main демонстрационной программы:
Каждый вызов метода Next возвращает значение в диапазоне [0.0, 1.0) — больше или равно 0.0 и строго меньше 1.0. Шаблон (int)(hi – lo) * Next + lo) будет возвращать целое число в диапазоне [lo, hi–1].
Алгоритм Лемера весьма эффективен, и в простых сценариях я обычно выбираю именно его. Но заметьте, что ни один алгоритм из представленных в этой статье не обладает надежностью криптографического уровня и что их следует применять только в ситуациях, где не требуется статической строгости (statistical rigor).
Алгоритм Вичмана-Хилла
Этот алгоритм датируется 1982 годом. Идея Вичмана-Хилла заключается в генерации трех предварительных результатов и последующего их объединения в один финальный результат. Код, реализующий алгоритм Вичмана-Хилла, представлен на рис. 3. Демонстрационный код основан на статье Б. А. Вичмана (B. A. Wichmann) и А. Д. Хилла (I. D. Hill) «Algorithm AS 183: An Efficient and Portable Pseudo-Random Number Generator».
Рис. 3. Реализация алгоритма Вичмана-Хилла
Поскольку алгоритм Вичмана-Хилла использует три разных генерирующих уравнения, он требует трех начальных значений. В этом алгоритме три m-значения равны 30269, 30307 и 30323, поэтому вам понадобятся три начальных значения в диапазоне [1, 30000]. Вы могли бы написать конструктор, принимающий эти три значения, но тогда вы получили бы несколько раздражающий программный интерфейс. В демонстрации применяется параметр с одним начальным значением, генерирующим три рабочих зародыша.
Вызов RNG Вичмана-Хилла осуществляется по тому же шаблону, что и других демонстрационных RNG:
Алгоритм Вичмана-Хилла лишь немного труднее в реализации, чем алгоритм Лемера. Преимущество первого над вторым в том, что алгоритм Вичмана-Хилла генерирует более длинную последовательность (более 6 000 000 000 000 значений) до того, как начнет повторяться.
Линейный конгруэнтный алгоритм
Оказывается, и алгоритм Лемера, и алгоритм Вичмана-Хилла можно считать особыми случаями так называемого линейного конгруэнтного алгоритма (linear congruential, LC). Выраженный в виде уравнения, LC выглядит так:
Это точно соответствует алгоритму Лемера с добавлением дополнительной константы c. Включение c придает универсальному LC-алгоритму несколько лучшие статистические свойства по сравнению с алгоритмом Лемера. Демонстрационная реализация LC-алгоритма показана на рис. 4. Код основан на стандарте POSIX (Portable Operating System Interface).
Рис. 4. Реализация линейного конгруэнтного алгоритма
LC-алгоритм использует несколько битовых операций. Здесь идея в том, чтобы в базовых математических типах работать не с целым типом (32 бита), а с длинным целым (64 бита). По окончании 32 из этих битов (с 16-го по 47-й включительно) извлекаются и преобразуются в целое число. Этот подход дает более качественные результаты, чем при использовании просто 32 младших или старших битов, но за счет некоторого усложнения кодирования.
В демонстрации генератор случайных чисел LC вызывается так:
Заметьте, что в отличие от генераторов Лемера и Вичмана-Хилла генератор LC может принимать начальное значение 0. Конструктор в демонстрации LC копирует значение входного параметра seed непосредственно в член класса — поле seed. Многие распространенные реализации LC выполняют предварительные манипуляции над входным начальным значением, чтобы избежать генерации хорошо известных серий начальных значений.
Алгоритм Фибоначчи с запаздываниями
Этот алгоритм, выраженный уравнением, выглядит так:
Если на словах, то новое случайное число является тем, которое было сгенерировано 7 раз назад, плюс случайное число, сгенерированное 10 раз назад, и деленное по модулю на большое значение m. Значения (7, 10) можно изменять, как я вскоре поясню.
Допустим, что в некий момент времени последовательность сгенерированных чисел следующая:
где 561 — самое последнее из сгенерированных значений. Если m = 100, то следующим случайным числом будет:
Заметьте, что в любой момент вам всегда нужны 10 самых последних сгенерированных значений. Поэтому ключевая задача в алгоритме Фибоначчи с запаздываниями состоит в генерации начальных значений, необходимых для запуска процесса. Демонстрационная реализация алгоритма Фибоначчи с запаздываниями приведена на рис. 5.
Рис. 5. Реализация алгоритма Фибоначчи с запаздываниями
Демонстрационный код использует предыдущие случайные числа X(i–7) и X(i–10) для генерации следующего случайного числа. В научно-исследовательской литературе по этой тематике значения (7, 10) обычно обозначаются (j, k). Существуют другие пары (j, k), которые можно применять для алгоритма Фибоначчи с запаздываниями. Несколько значений, рекомендованных в хорошо известной книге «Art of Computer Programming» (Addison-Wesley, 1968), — (24,55), (38,89), (37,100), (30,127), (83,258), (107,378).
Чтобы инициализировать (j, k) в RNG Фибоначчи с запаздываниями, вы должны предварительно заполнить список значениями k. Это можно сделать несколькими способами. Однако наименьшее из начальных значений k обязательно должно быть нечетным. В демонстрации применяется грубый метод копирования значения параметра seed для всех начальных значений k с последующим удалением первой 1000 сгенерированных значений. Если значение параметра seed четное, тогда первое из значений k выставляется равным 11 (произвольному нечетному числу).
Чтобы предотвратить арифметическое переполнение, метод Next использует тип long для вычислений и математическое свойство: (a + b) mod n = [(a mod n) + (b mod n)] mod n.
Заключение
Позвольте мне подчеркнуть, что все четыре RNG, представленные в этой статье, предназначены только для некритичных случаев применения. С учетом этого я прогнал все RNG через набор хорошо известных базовых тестов на степень случайности, и они прошли эти тесты. Но даже при этом коварство RNG всем хорошо известно, и время от времени даже в стандартных RNG обнаруживаются дефекты, иногда лишь спустя годы их использования. Например, в 1960-х годах IBM распространяла реализацию линейного конгруэнтного алгоритма под названием RANDU, которая, как оказалось, обладала невероятно плохими качествами. А в Microsoft Excel 2008 была выявлена ужасно проблемная реализация алгоритма Вичмана-Хилла.
Нынешний фаворит в генерации случайных чисел — алгоритм Фортуна (Fortuna) (названный в честь римской богини удачи). Алгоритм Фортуна был опубликован в 2003 году и основан на математической энтропии плюс сложных шифровальных методах, таких как AES (Advanced Encryption System).
Джеймс Маккафри (Dr. James McCaffrey) — работает на Microsoft Research в Редмонде (штат Вашингтон). Принимал участие в создании нескольких продуктов Microsoft, в том числе Internet Explorer и Bing. С ним можно связаться по адресу jammc@microsoft.com.
Выражаю благодарность за рецензирование статьи экспертам Microsoft Крису Ли (Chris Lee) и Кирку Олинику (Kirk Olynyk).