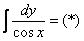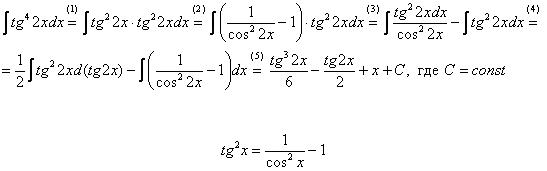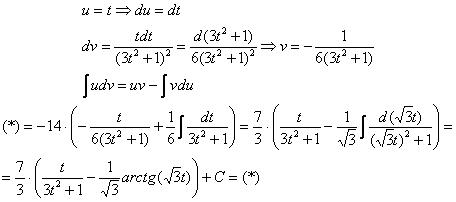Содержание
Интеграл от синуса
(largeint
ormalsize <sin x,dx>= – cos x + C)
Интеграл от косинуса
(largeint
ormalsize <cos x,dx>= sin x + C)
Интеграл от синуса в квадрате
(largeint
ormalsize <<<sin >^2>x,dx> = largefrac
ormalsize – largefrac<1><4>
ormalsize sin <2x>+ C)
Интеграл от косинуса в квадрате
(largeint
ormalsize <<<cos >^2>x,dx> = largefrac
ormalsize + largefrac<1><4>
ormalsize sin <2x>+ C)
Интеграл от синуса в кубе
(largeint
ormalsize <<<sin >^3>x,dx> = largefrac<1><3>
ormalsize<cos ^3>x – cos x + C = largefrac<1><<12>>
ormalsizecos <3x>- largefrac<3><4>
ormalsize cos x + C)
Интеграл от косинуса в кубе
(largeint
ormalsize <<<cos >^3>x,dx> = sin x – largefrac<1><3>
ormalsize<sin ^3>x + C = largefrac<1><<12>>
ormalsizesin <3x>+ largefrac<3><4>
ormalsize sin x + C)
Интеграл от секанса
(largeint <frac<
ormalsize = largeint
ormalsize <sec x,dx>= ln left| < an left( <largefrac
ormalsize + largefrac<pi ><4>
ormalsize>
ight)>
ight| + C)
Интеграл от косеканса
(largeint <frac<
ormalsize = largeint
ormalsize <csc x,dx>= ln left| < an <largefrac
ormalsize>>
ight| + C)
Интеграл от секанса в квадрате
(largeint <frac<
ormalsize = largeint
ormalsize <<<sec >^2>x,dx> = an x + C)
Интеграл от косеканса в квадрате
(largeint <frac<
ormalsize = largeint
ormalsize <<<csc >^2>x,dx> = -cot x + C)
Интеграл от секанса в кубе
(largeint <frac<
ormalsize = largeint
ormalsize <<<sec >^3>xdx> = largefrac<<sin x>><<2<<cos >^2>x>>
ormalsize + largefrac<1><2>
ormalsizeln left| < an left( <largefrac
ormalsize + largefrac<pi ><4>>
ormalsize
ight)>
ight| + C)
Интеграл от косеканса в кубе
(largeint <frac<
ormalsize = largeint
ormalsize <<<csc >^3>xdx> = -largefrac<<cos x>><<2<<sin >^2>x>>
ormalsize + largefrac<1><2>
ormalsizeln left| < an largefrac
ormalsize>
ight| + C)
Интеграл от произведения синуса и косинуса
(largeint
ormalsize <sin xcos x,dx>= – largefrac<1><4>
ormalsizecos <2x>+ C)
Интеграл от произведения синуса в квадрате и косинуса
(largeint
ormalsize <<<sin >^2>xcos x ,dx> = largefrac<1><3>
ormalsize <sin^3>x + C)
Интеграл от произведения косинуса в квадрате и синуса
(largeint
ormalsize <<<cos >^2>xsin x ,dx> = -largefrac<1><3>
ormalsize <cos^3>x + C)
Интеграл от произведения квадратов синуса и косинуса
(largeint
ormalsize <<<sin >^2>x,<<cos >^2>x,dx> = largefrac
ormalsize – largefrac<1><<32>>
ormalsize sin <4x>+ C)
Интеграл от тангенса
(largeint
ormalsize < an x,dx>= – ln left| <cos x>
ight| + C)
(largeint
ormalsize <largefrac<<sin x>><<<<cos >^2>x>>
ormalsize dx> = largefrac<1><<cos x>>
ormalsize + C = sec x + C)
(largeint
ormalsize <largefrac<<<<sin >^2>x>><<cos x>>
ormalsize dx> = ln left| < an left( <largefrac
ormalsize + largefrac<pi ><4>
ormalsize>
ight)>
ight| – sin x + C)
Интеграл от тангенса в квадрате
(largeint
ormalsize <<< an >^2>x,dx> = an x – x + C)
Интеграл от котангенса
(largeint
ormalsize <cot x,dx>= ln left| <sin x>
ight| + C)
(largeint
ormalsize <largefrac<<cos x>><<<<sin >^2>x>>
ormalsize dx> = – largefrac<1><<sin x>>
ormalsize + C = – csc x + C)
Интеграл от котангенса в квадрате
(largeint
ormalsize <<<cot >^2>x,dx> = – cot x – x + C)
(largeint
ormalsize <largefrac<
ormalsize> = – largefrac<1><<sin x>>
ormalsize + ln left| < an left( <largefrac
ormalsize + largefrac<pi ><4>>
ormalsize
ight)>
ight| + C)
Подынтегральное выражение можно преобразовать из произведения тригонометрических функций в сумму
Рассмотрим интегралы, в которых подынтегральная функция представляет собой произведение синусов и косинусов первой степени от икса, умноженного на разные множители, то есть интегралы вида

Воспользовавшись известными тригонометрическими формулами



можно преобразовать каждое из произведений в интегралах вида (31) в алгебраическую сумму и проинтегрировать по формулам


Решение. По формуле (2) при
Применяя далее формулу (5), получим
Решение. По формуле (3) при 
Применяя далее формулу (6), получим
Решение. По формуле (4) при 
Применяя формулу (6), получим
Интеграл произведения степеней синуса и косинуса одного и того же аргумента
Рассмотрим теперь интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.е.

В частных случаях один из показателей (m или n) может равняться нулю.
При интегрировании таких функций используется то, что чётную степень косинуса можно выразить через синус, а дифференциал синуса равен cos x dx (или чётную степень синуса можно выразить через косинус, а дифференциал косинуса равен – sin x dx ) .
Следует различать два случая: 1) хотя бы один из показателей m и n нечётный; 2) оба показателя чётные.
Пусть имеет место первый случай, а именно показатель n = 2k + 1 – нечётный. Тогда, учитывая, что
Подынтегральное выражение представлено в таком виде, что одна его часть – функция только синуса, а другая – дифференциал синуса. Теперь с помощью замены переменной t = sin x решение сводится к интегрированию многочлена относительно t. Если же только степень m нечётна, то поступают аналогично, выделяя множитель sinx, выражая остальную часть подынтегральной функции через cos x и полагая t = cos x . Этот приём можно использовать и при интегрировании частного степеней синуса и косинуса, когда хотя бы один из показателей – нечётный. Всё дело в том, что частное степеней синуса и косинуса – это частный случай их произведения: когда тригонометрическая функция находится в знаменателе подынтегрального выражения, её степень – отрицательная. Но бывают и случаи частного тригонометрических функций, когда их степени – только чётные. О них – следующем абзаце.
Если же оба показателя m и n – чётные, то, используя тригонометрические формулы
понижают показатели степени синуса и косинуса, после чего получится интеграл того же типа, что и выше. Поэтому интегрирование следует продолжать по той же схеме. Если же один из чётных показателей – отрицательный, то есть рассматривается частное чётных степеней синуса и косинуса, то данная схема не годится. Тогда используется замена переменной в зависимости от того, как можно преобразовать подынтегральное выражение. Такой случай будет рассмотрен в следующем параграфе.
Пример 4. Найти интеграл от тригонометрической функции
Решение. Показатель степени косинуса – нечётный. Поэтому представим
и произведём замену переменной t = sin x (тогда dt = cos x dx ). Тогда получим
Возвращаясь к старой переменной, окончательно найдём
Пример 5. Найти интеграл от тригонометрической функции

Решение. Показатель степени косинуса, как и в предыдущем примере – нечётный, но больше. Представим
и произведём замену переменной t = sin x (тогда dt = cos x dx ). Тогда получим

Возвращаясь к старой переменной, получаем решение
Пример 6. Найти интеграл от тригонометрической функции
Решение. Показатели степени синуса и косинуса – чётные. Поэтому преобразуем подынтегральную функцию так:
Во втором интеграле произведём замену переменной, полагая t = sin2x . Тогда (1/2)dt = cos2x dx . Следовательно,
Найти интеграл от тригонометрической функции самостоятельно, а затем посмотреть решение
Пример 7. Найти интеграл от тригонометрической функции

Использование метода замены переменой
Метод замены переменной при интегировании тригонометрических функций можно применять в случаях, когда в подынтегральном выражении присутствует только синус или только косинус, произведение синуса и косинуса, в котором или синус или косинус – в первой степени, тангенс или котангенс, а также частное чётных степеней синуса и косинуса одного и того же аргумента. При этом можно производить перестановки не только sinx = t и sinx = t , но и tgx = t и ctgx = t .
Пример 8. Найти интеграл от тригонометрической функции

Решение. Произведём замену переменной: 


Возвращаясь к первоначальной переменной, окончательно получаем:
Пример 9. Найти интеграл от тригонометрической функции

Решение. Преобразуем тангенс в отношение синуса и косинуса:

Произведём замену переменной: 


Возвращаясь к первоначальной переменной, окончательно получаем:

Пример 10. Найти интеграл от тригонометрической функции

Решение. Произведём замену переменной: 

Преобразуем подынтегральное выражение, чтобы применить тригонометрическое тождество 
Производим замену переменной, не забывая перед интегралом поставить знак минус (смотрите выше, чему равно dt ). Далее раскладываем подынтегральное выражение на множители и интегрируем по таблице:

Возвращаясь к первоначальной переменной, окончательно получаем:

Найти интеграл от тригонометрической функции самостоятельно, а затем посмотреть решение
Пример 11. Найти интеграл от тригонометрической функции

Универсальная тригонометрическая подстановка
Универсальную тригонометрическую подстановку можно применять в случаях, когда подынтегральное выражение не подпадает под случаи, разобранные в предыдущих параграфах. В основном, когда синус или косинус (или и то, и другое) находятся в знаменателе дроби. Доказано, что синус и косинус можно заменить другим выражением, содержащим тангенс половины исходного угла следующим образом:
где 
Тогда 
Но заметим, что универсальная тригонометрическая подстановка часто влечёт за собой довольно сложные алгебраические преобразования, поэтому её лучше применять, когда никакой другой метод не работает. Разберём примеры, когда вместе с универсальной тригонометрической подстановкой используются подведение под знак дифференциала и метод неопределённых коэффициентов.
Пример 12. Найти интеграл от тригонометрической функции

Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой. Тогда 
Дроби в числителе и знаменателе умножаем на 
Чтобы в результате преобразований прийти к табличному интегралу, попытаемся получить в знаменателе полный квадрат. Для этого умножим числитель и знаменатель подынтегрального выражения на 2. Применяем интегрирование подведением под знак дифференциала. Получим
К полученному результату преобразований можем теперь применить табличный интеграл 21. В результате получаем окончательное решение:

Пример 13. Найти интеграл от тригонометрической функции

Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой. Тогда 
Дроби в числителе и знаменателе умножаем на 

Чтобы в результате преобразований прийти к табличному интегралу, попытаемся получить в знаменателе полный квадрат. Для этого умножим числитель и знаменатель подынтегрального выражения на 3. Применяем интегрирование подведением под знак дифференциала. Получим
К полученному результату преобразований можем теперь применить табличный интеграл 21. В результате получаем окончательное решение:

Пример 14. Найти интеграл от тригонометрической функции

Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой. Тогда
Используем метод неопределённых коэффициентов. Получим следующее подынтегральное выражение:
Чтобы найти коэффициенты, решим систему уравнений:
Используем подведение под знак дифференциала:
К последнему слагаемому применяем замену переменной 

Преобразуем и вернём на место первоначальную переменную и окончательно получим решение:
Это пример для самостоятельного решения. В образце решения дважды последовательно использована вышеупомянутая формула.
Если под степенью находится неразложимый на множители квадратный трехчлен, то решение сводится к двучлену путем выделения полного квадрата, например:
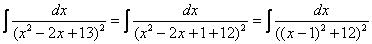
Далее следует «безболезненная» линейная замена 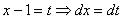
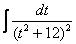
Что делать, если дополнительно в числителе есть многочлен? В этом случае используется метод неопределенных коэффициентов, и подынтегральная функция раскладывается в сумму дробей. Если такой интеграл встретится, смотрите учебник – там всё просто.
Интегрирование сложных тригонометрических функций
На уроке Интегралы от тригонометрических функций мы разобрали интеграл от тангенса в квадрате. В том примере для нахождения интеграла мы применяли тригонометрическую формулу

Интеграл от тангенса в четвертой, пятой степени (редко в более высоких степенях) решается с помощью этой же формулы!
Пример 15 Найти неопределенный интеграл
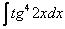
Идея решения подобных интегралов состоит в том, чтобы с помощью формулы 
(1) Готовим подынтегральную функцию к применению формулы.
(2) Для одного из множителей используем формулу
(3) Раскрываем скобки и сразу же используем свойство линейности неопределенного интеграла.
(4) В первом интеграле используем метод подведения функции под знак дифференциала , во втором интеграле еще раз используем формулу

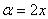
(5) Берём все три интеграла и получаем ответ.
Найти неопределенный интеграл
Это пример для самостоятельного решения.
Для котангенса существует аналогичная формула:

Если возникли затруднения или недопонимание, следует вернуться к уроку Интегралы от тригонометрических функций . На вышеупомянутом уроке мы рассматривали универсальную тригонометрическую подстановку для решения определенного вида интегралов от тригонометрических функций. Недостаток универсальной тригонометрической подстановки заключается в том, что при её применении часто возникают громоздкие интегралы с трудными вычислениями. И в ряде случаев универсальной тригонометрической подстановки можно избежать! Рассмотрим еще один канонический пример – интеграл от единицы, деленной на синус:
Пример 17 Найти неопределенный интеграл
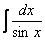
Здесь можно использовать универсальную тригонометрическую подстановку и получить ответ, но существует более рациональный путь. Приведём это решение с комментариями к каждому шагу:
(1) Используем тригонометрическую формулу синуса двойного угла
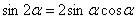
(2) Проводим искусственное преобразование: В знаменателе делим и умножаем на
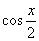
(3) По известной формуле в знаменателе превращаем дробь в тангенс.
(4) Подводим функцию под знак дифференциала.
(5) Берём интеграл.
Пример 18 Найти неопределенный интеграл
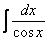
Указание: Самым первым действием следует использовать формулу прив е дения
и аккуратно провести аналогичные предыдущему примеру действия.
Пример 19 Найти неопределенный интеграл
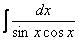
Ну, это совсем простой пример. Полные решения и ответы в конце урока.
Думаем, теперь ни у кого не возникнет проблем с интегралами:

В чём состоит идея метода? Идея состоит в том, чтобы с помощью тождественных преобразований и тригонометрических формул организовать в подынтегральной функции только тангенсы и производную тангенса
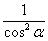
То есть, речь идет о замене:

В Примерах 17-19 мы фактически и применяли данную замену, но интегралы были настолько просты, что дело обошлось эквивалентным действием – подведением функции под знак дифференциала.
Примечание: аналогичные рассуждения можно провести и для котангенса.
Существует и формальное правило для применения вышеуказанной замены:
Если сумма степеней косинуса и синуса – целое отрицательное число, то интеграл можно свести к тангенсам и его производной .
Для интеграла 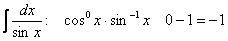
Для интеграла 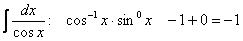
Для интеграла 
Пример 20 Найти неопределенный интеграл
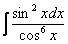
Сумма степеней синуса и косинуса 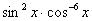
(1) Преобразуем знаменатель.
(2) По известной формуле получаем 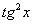
(3) Преобразуем знаменатель.
(4) Используем формулу
(5) Подводим функцию под знак дифференциала.
(6) Проводим замену 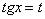
Далее берётся простой интеграл и проводится обратная замена.
Пример 21 Найти неопределенный интеграл
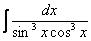
Это пример для самостоятельного решения.
Пример 22 Найти неопределенный интеграл
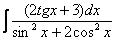
В этом интеграле изначально присутствует тангенс, что сразу наталкивает на уже знакомую мысль:
Пара творческих примеров для самостоятельного решения:
Пример 23 Найти неопределенный интеграл
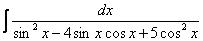
Пример 24 Найти неопределенный интеграл
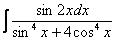
Да, в них, конечно, можно понизить степени синуса, косинуса, использовать универсальную тригонометрическую подстановку, но решение будет гораздо эффективнее и короче, если его провести через тангенсы. Полное решение и ответы в конце урока.
Переходим к заключительному пункту путешествия в мир сложных интегралов:
Интеграл от корня из дроби
Интеграл, который мы рассмотрим, встречается достаточно редко, но я буду очень рад, если единственный пример данного параграфа вам поможет.
Корнями всё начиналось, корнями и закончится. Рассмотрим неопределенный интеграл:

В подынтегральной функции у нас находится корень, а под корнем – дробь, в числителе и знаменателе которой располагаются линейные функции.
Метод стар – необходимо избавиться от корня. Стар и уныл, но сейчас станет веселее, поскольку придется проводить непростую замену.
Замена, с помощью которой мы гарантированно избавимся от корня, такова:

Теперь нужно выразить «икс» и найти, чему равен дифференциал dx . Выражаем «икс»:
Теперь найдем дифференциал:
Зачем были эти нелепые скучные телодвижения?
Мы вывели готовые формулы, которыми можно пользовать при решении интеграла вида
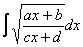
Формулы замены таковы:
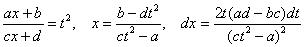
Пример 25 Найти неопределенный интеграл
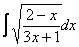

В данном примере: a =-1, b = 2, c = 3, d = 1. Тогда для dx имеем:
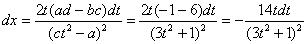

Такой интеграл, кстати, уже фигурировал в Примере 13. Интегрируем по частям:
Проведем обратную замену. Если изначально
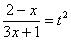
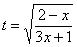
Некоторым страшно, а я это продифференцировал, ответ верный! Иногда встречаются интегралы вида
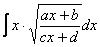
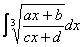
но это нужно быть либо слишком умным, либо попасть под раздачу.
Идея та же – избавиться от корня, причем во втором случае, как все догадались, следует проводить подстановку

и самостоятельно выводить, чему будет равняться дифференциал dx . Теперь вам практически любой интеграл по силам, успехов!
Решения и ответы:
Пример 2: Решение:
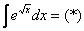
Интегрируем по частям:

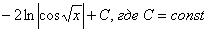
Пример 6: Решение:
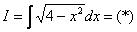
Интегрируем по частям:
Пример 8: Решение:
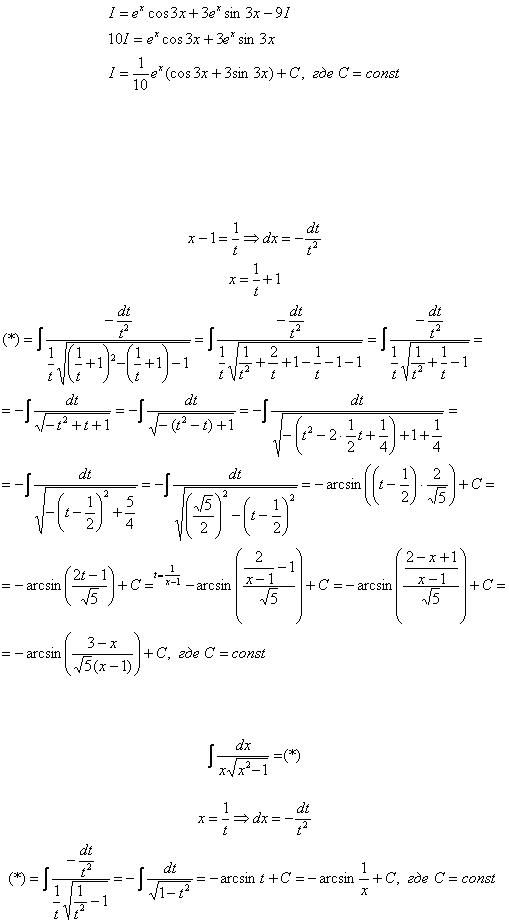
Дважды интегрируем по частям и сводим интеграл к самому себе:
Пример 10: Решение:
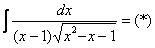
Пример 11: Решение:
Пример 12: Решение:
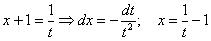
Пример 14: Решение:
Дважды используем рекуррентную формулу
Пример 16: Решение:
Пример 18: Решение: