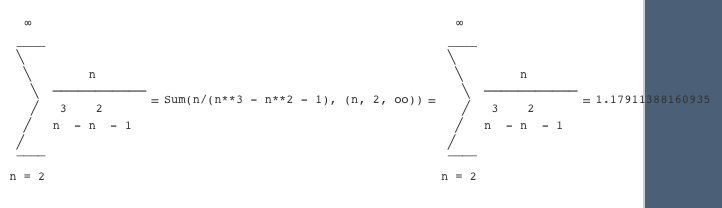Содержание
Даны два ряда (sumlimits_
ormalsize> ) сходится при (p > 1) и расходится при (0 1.) Применяя далее признак сравнения, находим [ <sumlimits_
ormalsize>>>><<>>> > <le sumlimits_
ormalsize>) сходится как обобщенный гармонический ряд с показателем степени (p = 2,) то исходный ряд также сходится.
Воспользуемся признаком сравнения. Заметим, что (largefrac <<- 1>><<>>
ormalsize 1) и, следовательно, сходится.
Таким образом, исходный ряд сходится по признаку сравнения.
Можно заметить, что ( – 3 frac<1><<>>,>;; <Rightarrow frac<<>> <<- 3>> > frac<<>><<>> = frac<1>
ormalsize> ) − гармонический ряд, то он расходится. Следовательно, исходный ряд также расходится по признаку сравнения.
Перед началом работы с этой темой советую посмотреть раздел с терминологией для числовых рядов. Особенно стоит обратить внимание на понятие общего члена ряда и свойства числовых рядов (в частности, нам понадобятся свойства №3 и №4). Если у вас есть сомнения в правильности выбора признака сходимости, советую глянуть тему "Выбор признака сходимости числовых рядов".
Признаки сравнения применяются для исследования числовых рядов, члены которых неотрицательны, т.е. больше или равны нулю. Такие ряды называются положительными (в части литературы – неотрицательными или знакоположительными). Именно такие ряды мы и станем рассматривать в данной теме.
Первый признак сравнения (или первая теорема сравнения) формулируется следующим образом:
Первый признак сравнения
Упрощённо говоря, если ряд с меньшими членами не имеет суммы (расходится), то и ряд с бо́льшими членами тоже будет расходиться. И это логично, ибо если исходная сумма была бесконечно большой, то после увеличения слагаемых она такой и останется.
Ну, и если ряд с бо́льшими членами имеет сумму (сходится), то и ряд с меньшими членами тоже будет сходиться.
Признак сравнения можно сформулировать также и в иной форме. Обычно говорят, что это второй признак сравнения (или вторая теорема сравнения). Иногда его называют предельным признаком сравнения или признаком сравнения в предельной форме. Формулировка его такова:
Второй признак сравнения
Особо стоит обратить внимание на случай $alpha=1$, т.е. ряд $sumlimits_^<infty>frac<1>=sumlimits_^<infty>frac<1>
Кроме того, частенько для сравнения используется ряд такого вида:
Этот ряд представляет собой сумму членов геометрической прогрессии с первым членом $b_1=a$ и знаменателем $q$. Этот ряд сходится если $|q| 0$ и $2n^3+5n^2-4 > 0$, то $u_n > 0$. Следовательно, наш ряд является положительным. Кстати сказать, для положительного ряда достаточно выполнения условия $u_n≥ 0$. Однако для нашего ряда мы можем записать более точно: $u_n > 0$.
Для начала неплохо бы проверить выполнение необходимого условия сходимости, т.е. найти $lim_u_n$. Вдруг нам повезёт и окажется, что $lim_u_n
eq 0$? Тогда ряд будет расходиться, и решение на этом закончится. При нахождении предела будем использовать метод, описанный в теме "Предел отношения двух многочленов". В процессе решения разделим числитель и знаменатель на $n^3$:
Так как $lim_u_n=0$, то никакого вывода про сходимость нашего ряда мы сделать не в состоянии. Ряд может как сходиться, так и расходиться. Попробуем применить признаки сравнения.
Для того, чтобы эти признаки использовать, нам понадобится ряд, с которым станем сравнивать. Чтобы выбрать ряд для сравнения, поисследуем поведение общего члена заданного нам ряда при $n oinfty$. Это можно сделать с помощью несколько неформальных рассуждений. Так как эти рассуждения, возможно, будут интересны не всем читателям, то я скрою их под примечание.
Как выбрать ряд для сравнения? показатьскрыть
Я не буду касаться такой темы как порядок роста, просто приведу некие общие соображения. Давайте посмотрим на общий член ряда повнимательнее. Сначала обратимся, например, к знаменателю. В знаменателе общего члена ряда расположены степени $n^3$, $n^2$ и число -4. Номер $n$ всё увеличивается, стремясь в бесконечность. Вопрос: какой элемент ($n^3$ или $n^2$) с возрастанием номера $n$ будет расти быстрее прочих?
Ответ здесь прост: наиболее быстро будет увеличивать свои значения именно $n^3$. Например, когда $n=100$, то $n^2=10,000$, а $n^3=1,000,000$. И этот разрыв между значениями $n^2$ и $n^3$ будет всё больше и больше. Поэтому все слагаемые знаменателя, кроме тех, что содержат $n^3$, мы мысленно отбросим. В числителе также проведем подобную процедуру "отбрасывания", оставив лишь $9n$ (число 7 в числителе явно не сыграет никакой роли по сравнению с $9n$). Таким образом дробь $frac<9n+7><2n^3+5n^2-4>$ после всех отбрасываний станет такой: $frac<9n><2n^3>=frac<9><2>cdotfrac<1>$. Иными словами, если $n oinfty$, то общий член ряда будет крайне мало отличаться от выражения $frac<9><2>cdotfrac<1>$.
Множитель $frac<9><2>$ можно также отбросить, ибо он не влияет на сходимость. И останется после такой "очистки" лишь $frac<1>$. А что мы можем сказать про ряд с общим членом $v_n=frac<1>$? Это обобщенный гармонический ряд. В знаменателе общего члена этого ряда степень $n$ равна 2, поэтому так как $2 > 1$, то ряд $sumlimits_^<infty>frac<1>$ сходится.
Вот с этим сходящимся рядом $sumlimits_^<infty>frac<1>$ мы и станем сравнивать заданный нам ряд $sumlimits_^<infty>frac<9n+7><2n^3+5n^2-4>$. По сути, мы уже неформально решили задачу: наш ряд будет сходиться. Осталось лишь показать это строгими рассуждениями.
Рассмотрим, как решить нашу задачу с помощью как первого, так и второго признаков сравнения.
Решение с помощью первого признака сравнения
Итак, общий член ряда таков: $u_n=frac<9n+7><2n^3+5n^2-4>$. Неформальными рассуждениями (скрытыми выше под примечание) мы пришли к выводу, что наш ряд сходится. Для этого случая применяется второй пункт первого признака сравнения. Нам нужно показать, что общий член нашего ряда удовлетворяет неравенству $frac<9n+7><2n^3+5n^2-4>≤ v_n$, при этом ряд $sumlimits_^<infty>v_n$ сходится. Тогда и заданный нам ряд будет сходиться.
Станем увеличивать дробь $frac<9n+7><2n^3+5n^2-4>$. Наша цель: привести данную дробь к виду $frac<1>$. Почему именно к этому виду? Для ответа на данный вопрос прошу раскрыть примечание выше.
Чтобы увеличить некую дробь, есть два пути: увеличить числитель или уменьшить знаменатель. Согласитесь, что так как $n≥ 1$, то $9n+7 ≥ 9n+7n=16n$. Следовательно, если мы в числителе вместо $9n+7$ разместим выражение $16n$, то увеличим рассматриваемую дробь:
Пойдём далее и поработаем со знаменателем. Чтобы увеличить дробь, знаменатель нужно уменьшить. Например, можно рассудить так: мы знаем, что $n≥ 1$. Тогда $5n^2-4 > 0$. Значит, если мы отбросим в знаменателе выражение $5n^2-4$, то знаменатель уменьшится. Следовательно, наша дробь увеличится. Продолжим предыдущее неравенство:
Как и в предыдущем примере, попробуем проверить выполнение необходимого условия сходимости, т.е. найдём $lim_u_n$. При нахождении предела будем использовать метод, описанный в теме "Предел отношения двух многочленов". В ходе решения разделим и числитель и знаменатель на $n^4$:
Так как $lim_u_n=0$, то никакого вывода про сходимость нашего ряда мы сделать не в состоянии. Ряд может как сходиться, так и расходиться. Попробуем применить признаки сравнения.
Выясним, с каким же рядом нужно сравнивать заданный в условии ряд. Попробуем отбросить "лишние" элементы числителя и знаменателя точно так же, как это было сделано в примере №1. Останется у нас такая дробь: $frac<4n^3>=frac<4><9>cdotfrac<1>
Решение с помощью первого признака сравнения
Неформальными рассуждениями, проведенными выше, мы пришли к выводу, что наш ряд расходится. Для этого случая применяется первый пункт первого признака сравнения. Нам нужно показать, что общий член нашего ряда удовлетворяет неравенству $v_n≤ frac<4n^3+2n+9>$, при этом ряд $sumlimits_^<infty>v_n$ расходится. Тогда и заданный нам ряд будет расходиться.
Станем уменьшать дробь $frac<4n^3+2n+9>$. Наша цель: привести данную дробь к виду $frac<1>
Чтобы уменьшить некую дробь, есть два пути: уменьшить числитель или увеличить знаменатель. Так как $n≥ 1$, то $2n+9 > 0$. Поэтому если мы отбросим в числителе $2n+9$, то уменьшим числитель, тем самым уменьшив рассматриваемую дробь:
Поработаем с знаменателем. Если мы его увеличим, то дробь уменьшится. Так как $n≥ 1$, то $3n+5≤ 3n+5n=8n$. Итак, если мы вместо $3n+5$ запишем $8n$, то знаменатель увеличится:
Дальнейшие рассуждения стандартны: так как ряд $sumlimits_^<infty>frac<1>
ight)$. Так как ряд $sumlimits_^<infty>left( frac<1><16>cdotfrac<1>
ight)$ расходится и $frac<4n^3+2n+9> > frac<1><16>cdotfrac<1>
Решение с помощью второго признака сравнения
Ранее мы уже выяснили, что сравнивать заданный ряд нужно с расходящимся рядом $sumlimits_^<infty>frac<1>
Так как $0 0$, т.е. наш ряд положительный. Точно так же, как и в предыдущих примерах, можно проверить выполнение необходимого условия сходимости, однако эта проверка лишь покажет, что $lim_u_n=0$. Т.е. ничего определённого про сходимость ряда сказать нельзя и нужно использовать иные критерии.
Для проверки сходимости заданного ряда с помощью признаков сравнения для начала составим ряд, с которым станем сравнивать. Попробуем отбросить "лишние" элементы числителя и знаменателя точно так же, как это было сделано в примерах №1 и №2. Останется у нас такая дробь:
Вот с рядом $sumlimits_^<infty>frac<1><4><3>>>$ мы и станем сравнивать заданный ряд. Так как $frac<4> <3>> 1$, то ряд $sumlimits_^<infty>frac<1><4><3>>>$ сходится. Следовательно, и наш ряд будет сходиться, нам осталось лишь показать это формально с помощью признаков сравнения.
Решение с помощью первого признака сравнения
Неформальными рассуждениями выше мы пришли к выводу, что наш ряд сходится. Для этого случая применяется второй пункт первого признака сравнения. Нам нужно показать, что общий член нашего ряда удовлетворяет неравенству $frac<5n^2-3><sqrt[3]<7n^<10>+2n^3-4>>≤ v_n$ и ряд $sumlimits_^<infty>v_n$ сходится. Тогда и заданный нам ряд будет сходиться.
Станем увеличивать дробь $frac<5n^2-3><sqrt[3]<7n^<10>+2n^3-4>>$. Наша цель: привести данную дробь к виду $frac<1><4><3>>>$.
Чтобы увеличить данную дробь, для начала увеличим числитель. Если мы отбросим число (-3), то числитель станет больше. А значит и сама дробь увеличится:
$$ frac<5n^2-3><sqrt[3]<7n^<10>+2n^3-4>> sqrt<2n-1>$, то $u_n > 0$, т.е. наш ряд положительный. Можно при желании проверить выполнение необходимого условия сходимости, однако эта проверка ничего не даст (предел $lim_u_n$ вычисляется по аналогии с примером №8 на этой странице), так как $lim_u_n=0$. Перейдём к применению признаков сравнения.
Перед тем, как применять некие признаки сравнения, выражение общего члена ряда лучше немного преобразовать. Тут поможет домножение на сопряжённое выражение, т.е. на $sqrt<2n+3>+sqrt<2n-1>$. Естественно, что если мы домножаем на некое выражение, то на него же обязаны и разделить. При упрощении нам поможет формула $(a-b)(a+b)=a^2-b^2$. Итак:
Теперь наш ряд имеет вид $sumlimits_^<infty>frac<4><sqrt<2n+3>+sqrt<2n-1>>$. Применяя рассуждения, аналогичные проведённым в предыдущих примерах, получим, что сравнивать наш ряд надо с рядом $sumlimits_^<infty>frac<1><sqrt
Решение с помощью первого признака сравнения
Неформальными рассуждениями выше мы пришли к выводу, что наш ряд расходится. Станем уменьшать дробь $frac<4><sqrt<2n+3>+sqrt<2n-1>>$. Так как $sqrt<2n+3>> sqrt<2n-1>$, то записав выражение $sqrt<2n+3>$ вместо $sqrt<2n-1>$ мы увеличим знаменатель, тем самым уменьшив дробь:
Увеличим знаменатель ещё раз. Так как $2n+3 frac<2><sqrt<2n+3>> > frac<2><sqrt<9n>>=frac<2><3>cdotfrac<1><sqrt
Так как ряд $sumlimits_^<infty>frac<1><sqrt
ight)$. Так как ряд $sumlimits_^<infty>left(frac<2><3>cdotfrac<1><sqrt
ight)$ расходится и $frac<4><sqrt<2n+3>+sqrt<2n-1>> >frac<2><3>cdotfrac<1><sqrt
Решение с помощью второго признака сравнения
Мы уже выяснили, что сравнивать заданный ряд нужно с расходящимся рядом $sumlimits_^<infty>frac<1><sqrt
Как исследовать сходимость числового ряда онлайн? Допустим нам надо исследовать ряд ∑n/(n^3-n^2-1), где n от 2 до +∞ Чтобы исследовать числовой ряд и его сходимость онлайн на сайте kontrolnaya-rabota.ru – нужно зайти на страницу
– нажимаем кнопку "Сумма ряда"
Получаем результат как на странице n/(n^3-n^2-1)
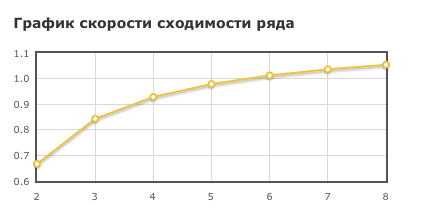
По данной ссылке вы увидете следующие интересные данные:
Опубликовано: Июнь 23, 2013
Тэги: ряд сходимость
© Контрольная работа РУ – примеры решения задач