Для чего нужен математический анализ

У меня непростые отношения с матанализом: с одной стороны он демонстрирует всю красоту и мощь математики, а с другой — агонию математического образования.

Математический анализ связывает различные темы в элегантной, но довольно сложной для ума манере. Ближайшая аналогия, которая приходит мне на ум, — Дарвиновская теория эволюции: стоит ее понять, и весь мир видится с позиции выживания. Вы понимаете, почему лекарства привели к резистентным микробам (выживает наиболее приспособленный). Вы понимаете, почему сахар и жир сладкие на вкус (вкус стимулирует потребление высококалорийных продуктов в условиях дефицита резервов организма). И все эти моменты складываются в единую, логическую картину.

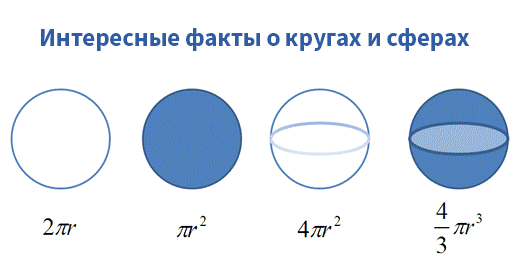
Матанализ таким же образом проливает свет на всю систему математики. Не кажется ли вам, что все эти формулы как-то связаны?

Так и есть. Но большинство из нас изучают эти формулы независимо друг от друга. Математический анализ позволяет начать с «длина окружности = 2 * π * r» и вывести остальные формулы для вычисления площади круга, сферы и даже объема шара — древним грекам очень бы пригодился подобный подход.

К сожалению, матанализ олицетворяет собой все трудности в изучении математики. Большинство уроков объясняются на натянутых, неправдоподобных примерах, заумных доказательствах и банальном заучивании, которое напрочь убивает интуицию.

Так действительно не должно происходить.

Математика, искусство и идеи

Кое-что я понял еще со школы: математика — не самая сложная часть математики; самое тяжелое — мотивация к ее освоению. Особенно, умение не терять энтузиазм, несмотря на:

• Преподавателей, больше сконцентрированных на штамповке публикаций и своей карьере, чем на преподавании
• Небеспочвенные опасения, что математика — это сложно, скучно, непопулярно или «не ваш предмет»
• Учебники и учебные планы, больше нацеленные на получение прибыли и хорошую статистику по тестированиям знаний, чем на пояснение сущности предмета.

«…если бы мне пришлось создавать механизм с единственной целью разрушить природное любопытство ребенка и его любовь к моделированию, вряд ли бы у меня получилось лучше, чем это уже реализовано — у меня бы просто не хватило фантазии, чтобы тягаться с такими бесчувственными, унылыми идеями, которые воплощены в современных методах изучения математики».

Представьте изучение изобразительного искусства так: Детки, никакого рисования в детском садике. Вместо этого, давайте-ка изучим химию лакокрасочных изделий, физику света и анатомию глаза. После 12 лет изучения этих аспектов, если дети (точнее уже подростки) всё еще не возненавидят искусство, они смогут начать рисовать самостоятельно. В конечном итоге, они теперь владеют полноценным фундаментом для того, чтобы начать уважать искусство. Верно?

Также и с поэзией. Представьте изучение этой цитаты (формулы):

«Но главное: будь верен сам себе; Тогда, как вслед за днем бывает ночь, Ты не изменишь и другим.» —Вильям Шекспир, Гамлет

Это элегантный способ сказать «будь собой» (и если это означает непочтительно писать о математике, пусть будет так). Но если бы мы рассматривали поэзию на уроке математики, вместо поиска смысла мы бы занялись подсчётом количества слогов, анализировали пятистопный ямб, разметкой существительных, глаголов и прилагательных.

Математика и поэзия — это как разные способы пояснить, охарактеризовать одно и то же. Формулы — это средства к достижению цели, способ выражения математической истины.

Мы забыли, что математика оперирует идеями, это не машинальное маниппулирование формулами, которые выражают эти идеи.

Ну это всё понятно, так в чем же твоя великая мысль?

Вот, что я не буду делать: я не буду пересказывать уже написанные учебники. Если вам нужны ответы здесь и сейчас, есть масса вебсайтов, видеоуроков и 20-минуток в помощь.

Вместо этого давайте освоим основные положения матанализа. Уравнений недостаточно — я хочу моментов озарения, чтобы вы действительно видели их смысл и понимали язык математики.

Формальный математический язык — это просто способ коммуникации. Графики, информативные анимированные модели и разговор простым языком могут дать больше знаний, чем целая страница заумных доказательств.

Но матанализ — это сложно!

Я думаю, что любой человек сможет понять основные положения матанализа. Нам не обязательно быть поэтами, чтобы наслаждаться произведениями Шекспира.

Вам будет гораздо проще, если вы знаете алгебру и интересуетесь математикой. Не так давно, чтение и письмо были работой специально обученных писцов. А сегодня это может сделать любой 10-летний ребенок. Почему?

Потому что мы этого ожидаем. Ожидания играют огромную роль в развитии возможностей. Так что ожидайте, что матанализ — это просто еще один предмет. Некоторые люди доходят до мельчайших подробностей (писатели/математики). Но остальные из нас могут просто восторгаться происходящим и попытаться его понять. Я бы хотел, чтобы каждый освоил основные понятия матанализа и сказал «Вот это да!».

Так о чем же матанализ?

Некоторые определяют матанализ как «область математики, которая изучает пределы, дифференцирование, интегрирование функций с одной или более переменных». Это определение верно, но оно совсем не полезно для новичков.

Вот мой ход: Матанализ делает с алгеброй то, что алгебра сделала с арифметикой.

• Арифметика — это манипуляция числами (сложение, умножение и т.д.).
• Алгебра находит связи между числами: a 2 + b 2 = c 2 — очень известная связь, описывающая соотношение сторон в прямоугольном треугольнике. Алгебра находит целые наборы чисел — если вы знаете a и b, вы можете вычислить и c.
• Матанализ находит связи между уравнениями: вы можете видеть, как одно уравнение (длина окружности = 2 * π * r) связано с другим (площадь круга = π * r 2 ).

Используя матанализ, мы можем спросить самые разные вопросы:

• Как уравнение растет и сокращается? Наращивается со временем?
• Когда оно достигнет самой высокой/низкой точки?
• Как мы используем переменные, которые постоянно меняются? (Тепло, движение, популяции, …).
• И многое, многое другое!

Алгебра и матанализ решают задачи вместе: матанализ находит новые уравнения, а алгебра их решает. Как эволюция, матанализ расширяет ваше понимание того, как работает матушка-природа.

Пример, пожалуйста

Представим, что мы знаем уравнение длины окружности (2 * π * r), и нам нужно найти площадь. С чего начнем?

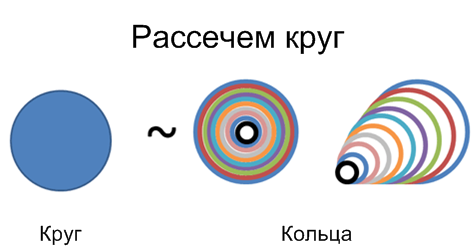
Представьте, что заполненный диск круга — это как набор матрешек.

Тут есть два способа нарисовать этот диск:

• Нарисовать окружность и закрасить ее
• Нарисовать набор колец толстым маркером

Количество «пространства» (площадь) должно быть одинаковым в обоих случаях, верно? И сколько пространства занимает кольцо?

Самое большое кольцо имеет радиус «r», и длина окружности кольца вычисляется как 2 * π * r. По мере того, как кольца уменьшаются, окружность также становится меньше, но всё равно сохраняется соотношение 2 * π * текущий радиус. Последнее кольцо больше похоже на булавочную головку, и длину окружности уже не вычислишь.

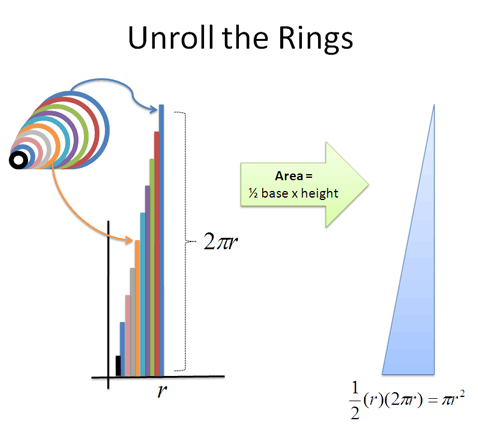
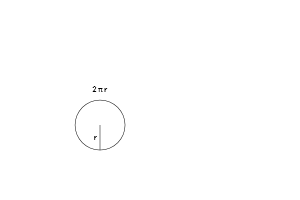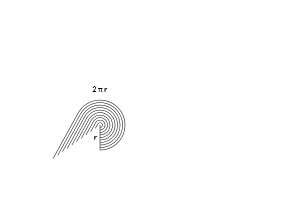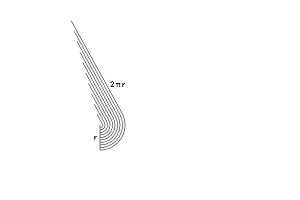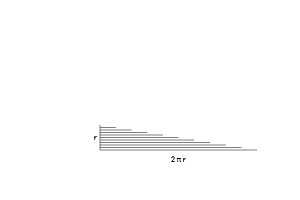
А теперь начинается самое интересное. Давайте раскрутим эти кольца и выровняем их. Что произойдет?

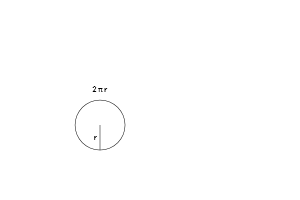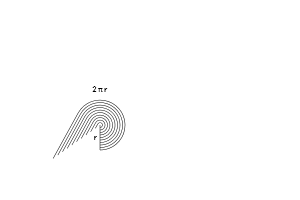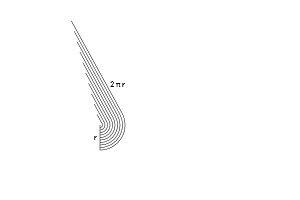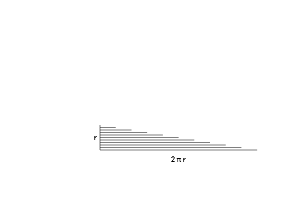
• У нас получится набор линий, который составит зубчатый треугольник. Но если взять более тонкие кольца, то треугольник становится уже менее зубчатым (об этом мы еще поговорим в других статьях).
• С одной стороны будет самое маленькое кольцо (0), а с другой — самое большое (2* π * r)
• Кольца имеют радиусы от 0 до «r». Для каждого возможного радиуса из этого диапазона (от 0 до r), мы просто помещаем раскрученное кольцо на свое место.
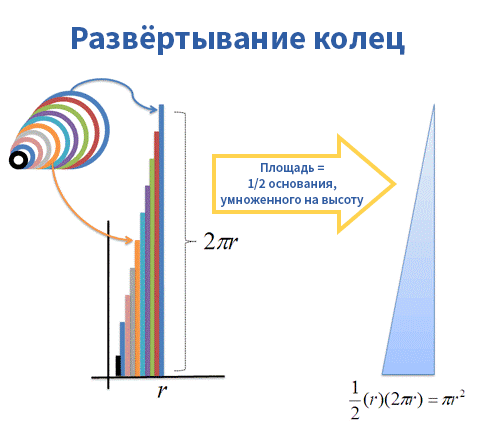
• Общая площадь «кольцевого треугольника» = 1/2 основания * высоту = 1/2 * r *(2 * π * r) = π * r 2 , а это и есть формула поиска площади круга!

Ух ты! Общая площадь колец = площадь треугольника = площадь круга!

Это был простой пример, но вы уловили основную идею? Мы взяли диск, разделили его, и сложили части вместе немного другим путем. Матанализ показал, что диск и кольцо тесно связаны друг с другом: диск — это действительно набор колец. Это очень популярная тема в матанализе: Большие предметы состоят из более мелких предметов. И иногда именно с этими мелкими предметами работается проще и понятнее.

Немного о примерах

Множество примеров в матанализе основано на физике. Это, конечно, замечательно, но бывает сложно их воспринимать: честно, далеко не всегда удается держать в голове разные физические формулы вроде формулы скорости объекта.

Я предпочитаю начать с простых визуальных примеров, потому что именно так и работает наш мозг. Кольцо/круг, которое мы исследовали — вы бы могли смоделировать то же самое из нескольких отрезков трубок разного диаметра: разделить их, выровнять и уложить в грубый треугольник, чтобы убедиться, что математика действительно работает. С простой физической формулой такое вряд ли удастся провернуть.

Немного о математической строгости (для фанатиков этой науки)

Я чувствую, как математики-педанты жгут свои клавиатуры. Поэтому я вставлю всего несколько слов о «строгости». Знаете ли вы, что мы не учим матанализ способами, которыми его открыл Ньютон или Лейбниц? Они использовали интуитивные идеи «флюксии» и «бесконечно малых величин», которые были заменены пределами, потому что «Конечно, это работает на практике. Но работает ли это в теории?».

Мы создали сложные механические модели, чтобы «точно» доказать матанализ, но мы утратили интуитивное восприятие предмета в процессе таких доказательств.

Мы смотрим на сладость сахара с точки зрения химии мозга, вместо того, чтобы пояснять это языком науки «В сахаре много энергии. Ешьте его».

Я не хочу (и не могу) преподавать матанализ студентам или обучать ученых. Но будет ли плохо, если каждый сможет понимать матанализ на том «неточном» уровне, на котором его понимал Ньютон? Чтобы это также изменило мир для вас, как когда-то изменило для него?

Преждевременная концентрация на точности рассредоточивает учеников и делает математику сложной для изучения. Вот хороший пример: число е технически определено пределом, но открыто оно было именно с помощью интуитивной догадки о росте. Натуральный логарифм может выглядеть как интеграл, или время, которому нужно расти. Какие объяснения лучше помогут новичкам?

Давайте немного порисуем от руки, а в химию погрузимся уже по ходу дела. Приятных вычислений.

Пройдя в универе полный курс математического анализа, а также линейную алгебру, комбинаторику, вычислительную математику, спец. главы мат. анализа, хотелось бы рассказать всем тем, кому это еще предстоит, и заодно попугать наших cute гуманитариев 🙂
Пост не сколько информативный, сколько дающий понять, что же из себя представляет тот самый матан.
Приготовьтесь к тому, что в матане вам придется узнать:

1) Есть такие комплексные числа – они как бы есть, но на самом деле их нет. Зачем они нужны, никто не знает, формальный предлог – расчет цепей переменного тока в ЭлТехе, ну и не только. На самом же деле, как я думаю, математики сами прутся от осознания, что есть что-то, чему они способны придать НУ ВООБЩЕ любое значение.

2) Если к бесконечности прибавить бесконечность, получится. бесконечность! Их еще можно делить друг на дружку, но это уже целая теорема. Небольшой спойлер – Лопиталь.

3) Делить на 0 можно. И что будет, если любое число разделить на ноль, как вы думаете. правильно, бесконечность!

4)Бесконечность бывает отрицательная и положительная, один из самых простых фактов.

5) Будьте готовы к самым разнообразным буковкам, так как преподаватель имеет право ввести свое обозначение, а вам придется его запоминать. Как следствие – в интернете будет чуть труднее искать решение домашки.

6) Отныне e(экспонента) – ваш бог, а натуральный логарифм – пастырь его! Серьезно, забудьте про всякие десятичные и логарифмы с заданным основанием, они понадобятся крайне редко.

6) Перемножать можно скалярно, а можно векторно(имеется ввиду вектора перемножать). Результат не одинаков, хотя операция – по сути одна и та же.

7) В отеле есть бесконечное количество однокомнатных комнат, все они заняты. Можно ли подселить в отель еще одного человека? – Да!

8) Дифференцировать и интегрировать вы будете не хуже, чем читать буковки в книжках. Притом сможете взять и тройной интеграл! А может, и четверной даже. вы будете способны по меньшей мере на многое, связанное с интегрированием и дифференцированием функций.

9)СЛАУ, ЧИ, ДУ – будут решаться без проблем, так как это лишь малая часть последующих вычислений. Не знаете что это? Я тоже не знал.

10) Вы изучите по меньшей мере 9/10 материала на mathprofi(не реклама, примеры решений, наиболее емкие и полезные).

11)Вычислить площадь любой фигуры через интеграл. Что? формула площади круга пирэр квадрат? Тру математики решают через интеграл!

12)Вы поймете, что математические формулы и вправду способны описать великолепие этого мира, но они будут слишком сложны, и сложны настолько, что некоторые из них не смогут подчиниться разуму человека. Потому математика -путь трудоемкий, и зачастую необоснованно сложный для восприятия. Дышите эмоциями.

небольшие краткие факты, что вспомнил. Не устаканивайтесь в чем-то одном, с вами был Ananasm)

Автор оригинала: Kalid Azad, перевёл: Филипп Сорокин.

Это третий перевод из серии статей на тему математического анализа, хотя по хронологии статья является первой. В дальнейшем переводы статей будут идти в соответствии с оригинальной хронологией, с пропуском уже переведённых.

Статья рассчитана на студентов и всех интересующихся высшей математикой, и представляет из себя введение в математический анализ с рассуждениями и интересными примерами его применения. Подойдёт и для чайников.

Введение

Мои отношения с математическим анализом строятся на любви и ненависти: этот предмет демонстрирует красоту математики и агонию математического образования.

Математический анализ связывает темы в элегантной, ломающей мозг манере. Моя ближайшая аналогия – теория эволюции Дарвина: однажды поняв, вы начинаете видеть природу с точки зрения выживания. Вы начинаете понимать, почему употребление лекарств приводит к появлению микробов, устойчивых к ним (выживание сильнейших). Вы понимаете, почему сахар и жир настолько вкусны (вкус, как поощрение за потребление высококалорийных продуктов в период дефицита). Всё начинает сходиться.

Математический анализ даёт такое же прозрение. Не кажется ли вам, что эти формулы каким-то образом связаны между собой?

Да, они связаны. Но большинство из нас изучает эти формулы по отдельности. Математический анализ помогает нам разобраться с каждой, начиная с длины окружности, равной 2πr – греки оценили бы это.

К сожалению, математический анализ может стать олицетворением того, что с математическим образованием что-то не так. Большинство уроков строятся на надуманных примерах, скрытых доказательствах и запоминании, что отбивает нашу интуицию и энтузиазм.

Так не должно быть.

Математика, искусство и идеи

Я кое-чему научился в школе: в математике самое трудное – не математика, а мотивация. В частности, мотивация оставаться воодушевлённым несмотря на:

– Преподавателей, которых больше заботит издание своих научных трудов, чем преподавание.

– Бытующие мнения, что математика – это сложно, скучно, непопулярно или «не ваш предмет».

– Учебники и программы обучения, которые больше заточены на получение прибыли и результатов тестирования, чем на понимание предмета.

«Плач математика» [pdf] является отличным эссе по этому вопросу, вызвавшим общественный резонанс (здесь было 3 ссылки, 2 из которых оказались битые – прим. пер.):

«…если бы мне пришлось разрабатывать механизм, предназначенный специально для разрушения естественного любопытства и любви к построению закономерностей у детей, я бы никогда не справился с этой работой так же хорошо, как это делается сейчас – у меня бы просто не хватило воображения, чтобы придумать настолько бессмысленные, душераздирающие идеи, которые составляют современное математическое образование.»

Представьте себе такое изучение искусства: Дети, никакого рисования руками в детском саду. Вместо этого, давайте-ка изучим химию красок, физику света и анатомию глаза. По прошествии 12 лет эти дети (которые уже подростки), если ещё не ненавидят искусство, смогут начать рисовать самостоятельно. В конце концов, у них есть «строгие, проверяемые» основы для того, чтобы начать ценить искусство. Правильно?

С поэзией также. Представьте себе процесс изучения этой цитаты (формулировки):

«Но главное – будь верен самому себе, и, следственно, как дважды два – четыре, ни перед кем не будешь ты фальшив.» – Вильям Шекспир, Гамлет

Математика и поэзия – это пальцы, указывающие на Луну. Не путайте палец с Луной. Формулы – это средство достижения цели, способ выразить математическую истину.

Мы забываем, что математика – это идеи, а не рутинные манипуляции с формулами, которые их выражают.

Ладно, приятель, в чём твоя отличная идея?

Дерзкие, да? Ну, чего я точно не буду делать, так это воссоздавать учебники по подобию уже существующих. Если вам прямо сейчас нужны ответы для какого-то серьёзного экзамена, то есть множество веб-сайтов, видеозаписей уроков и 20-минутных спринтов, чтобы помочь вам (оригинальные ссылки на англоязычные ресурсы – прим. пер.).

Вместо этого, давайте обсудим основные идеи математического анализа. Уравнений недостаточно – я хочу делиться «ага!»-моментами, от которых что-то щёлкает внутри.

Формальный математический язык – это лишь один из способов общения. Диаграммы, анимации и просто разговоры зачастую могут дать больше понимания, чем страница книги, полная доказательств.

Но мат. анализ – это сложно!

Я думаю, что любой сможет понять основные идеи математического анализа. Нам не нужно быть писателями, чтобы наслаждаться Шекспиром.

Это в пределах вашей досягаемости, если вы знаете алгебру и имеете простой интерес к математике. Не так давно чтение и письмо были работой опытных писцов. Но сегодня с этим может справиться и 10-летний ребёнок. Почему?

Потому что мы этого ожидаем. Ожидания играют огромную роль в том, что нам кажется возможным. Поэтому ожидайте, что мат. анализ – это просто ещё один предмет. Для немногих из нас это становится повседневной работой (писатели, математики). Но остальные всё ещё могут восхищаться тем, что происходит, и расширять свой кругозор.

Дело в том, как далеко ты намерен зайти. Я бы хотел, чтобы все смогли понять основные идеи математического анализа и сказали «вау».

Так о чём же мат. анализ?

Некоторые называют математический анализ «отраслью математики, которая занимается нахождением пределов, дифференцированием и интегрированием функций одной или нескольких переменных». Это правильно, но не несёт пользы для начинающих.

Вот моё мнение: мат. анализ делает с алгеброй то, что алгебра сделала с арифметикой.

– Арифметика – это манипулирование числами (сложение, умножение и т.д.).

– Алгебра находит закономерности между числами: a 2 + b 2 = c 2 – известное соотношение, описывающее стороны прямоугольного треугольника. Алгебра находит целые множества чисел – если вы знаете a и b, то вы можете найти c.

– Математический анализ находит закономерности между уравнениями: обратите внимание, как одно уравнение (длина окружности = 2πr) походит на другое (площадь окружности = πr 2 ).

При использовании мат. анализа у нас появляются новые вопросы:

– Как уравнение растёт и сжимается? Накапливается ли со временем?

– Когда оно достигает своего самого высокого/низкого значения?

– Как мы используем переменные, которые постоянно меняются? (тепло, движение, популяция, …).

– И множество других вопросов!

Алгебра и математический анализ – это дуэт для решения проблем: мат. анализ находит новые уравнения, а алгебра решает их. Как и эволюция, мат. анализ расширяет ваше понимание того, как работает природа.

Пример, пожалуйста

Давайте пройдёмся. Предположим, мы знаем уравнение для нахождения длины окружности (2πr) и хотим найти площадь круга. Что делать?

Представьте окружность в виде диска, который, как матрёшка, заполнен кольцами, идущими от краёв к центру.

Есть два способа изобразить диск:

– Нарисовать круг и закрасить его.

– Нарисовать множество колец толстым маркером.

Количество «пространства» (площади) должно быть одинаковым в обоих случаях, верно? Но как много пространства занимает одно кольцо?

Ну, самое большое кольцо имеет радиус «r» и длину окружности «2π», умноженную на текущий радиус. А последнее кольцо (самое маленькое – прим. пер.) больше похоже на точку без окружности.

Теперь всё выглядит совершенно необычно. Давайте развернём эти кольца и выстроим каждое из них в линию. Что произойдёт?

– Мы получим кучу линий, образующих неровный треугольник. Но чем тоньше и чаще будут расположены кольца, тем менее зубчатым будет треугольник (подробнее об этом в будущих статьях).

– С одной стороны будет наименьшее кольцо (0), а с другой наибольшее (2πr).

– У нас есть кольца, идущие от радиуса, равного 0, до равного «r». Для каждого возможного радиуса (от 0 до r) мы просто вставляем развёрнутое кольцо в соответствующее место.

– Общая площадь «кольцевого треугольника»: 1/2 основания * высоту = 1/2 (r) * (2πr) = πr 2 , что и является формулой для нахождения площади круга!

Вау! Площадь всех колец = Площадь треугольника = Площадь круга!

Это был быстрый пример, но вы ведь уловили основную мысль? Мы взяли диск, разделили его и сложили сегменты по-другому. Математический анализ показал нам, что диск и кольцо тесно связаны: диск на самом деле просто куча колец.

Это частая тема мат. анализа: Большие штуки складываются из маленьких частей. И иногда с маленькими частями проще работать.

Примечание о примерах

Многие примеры из математического анализа основаны на физике. Это здорово, но это же может быть трудно для понимания: ответьте честно, как часто вы вспоминаете уравнение для нахождения скорости объекта? Реже, чем раз в неделю.

Я предпочитаю начинать с физических, визуальных примеров, потому что так работает наш ум. Например, можем ли мы сделать такое же кольцо/круг, как в примере выше? Вы можете собрать такой круг из нескольких трубоочистителей, разделить на кольца и выпрямить их в грубый треугольник, чтобы проверить, действительно ли математика работает. С уравнением для вычисления скорости так не прокатит.

Примечание о соответствии канонам (для математических гиков)

Я чувствую, как математические педанты заводят свои клавиатуры. Несколько слов о «строгости».

Знаете ли вы, что мы изучаем не тот же самый мат. анализ, каким он был во времена открытия Ньютоном и Лейбницем? Они использовали интуитивные идеи «флюксий» и «бесконечных чисел», которые в последствии были вытеснены пределами, так как «Конечно, это работает на практике. Но работает ли это в теории?».

Мы создаём сложные механические конструкции, чтобы «в соответствии с канонами» доказывать математический анализ, но мы потеряли нашу интуитивное понимание в процессе.

Мы смотрим на сладость сахара, как на химическую реакцию в мозге вместо того, чтобы признать его способом природы сказать: «В этом много энергии. Ешь это.»

Я не хочу (и не могу) преподавать курсы анализа или обучать исследователей. Разве было бы плохо, если бы все понимали мат. анализ на «нестрогом» уровне, таким, каким его сделал Ньютон? Изменило ли бы это их взгляд на мир, как изменило у Ньютона?

Преждевременное внимание к «канонам» отталкивает студентов и затрудняет изучение математики. Пример: e технически определяется пределом, но интуитивное понимание экспоненциального роста в том, как он был открыт. Натуральный логарифм можно рассматривать, как интеграл, или как время, необходимое для роста. Какое из объяснений лучше подойдёт начинающим? (перевод двух статей из этого абзаца будет позже – прим. пер.)

Давайте немного порисуем руками и по ходу этого займёмся химией. Счастливой математики!