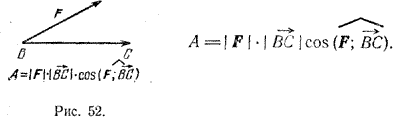Доказать свойства скалярного произведения векторов

Скалярное произведение векторов называют число, равное произведению дин этих векторов на косинус угла между ними.

Обозначение произведения векторов a → и b → имеет вид a → , b → . Преобразуем в формулу:

a → , b → = a → · b → · cos a → , b → ^ . a → и b → обозначают длины векторов, a → , b → ^ – обозначение угла между заданными векторами. Если хоть один вектор нулевой, то есть имеет значение 0, то и результат будет равен нулю, a → , b → = 0

При умножении вектора самого на себя, получим квадрат его дины:

a → , b → = a → · b → · cos a → , a → ^ = a → 2 · cos 0 = a → 2

Скалярное умножение вектора самого на себя называют скалярным квадратом.

Вычисляется по формуле:

a → , b → = a → · b → · cos a → , b → ^ .

Запись a → , b → = a → · b → · cos a → , b → ^ = a → · n p a → b → = b → · n p b → a → показывает, что n p b → a → – это числовая проекция a → на b → , n p a → a → – проекция b → на a → соостветсвенно.

Сформулируем определение произведения для двух векторов:

Скалярное произведение двух векторов a → на b → называют произведение длины вектора a → на проекцию b → на направление a → или произведение длины b → на проекцию a → соответственно.

Скалярное произведение в координатах

Вычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве.

Скаларное произведение двух векторов на плоскости, в трехмерном простарнстве называют сумму координат заданных векторов a → и b → .

При вычислении на плоскости скаларного произведения заданных векторов a → = ( a x , a y ) , b → = ( b x , b y ) в декартовой системе используют:

a → , b → = a x · b x + a y · b y ,

для трехмерного пространства применимо выражение:

a → , b → = a x · b x + a y · b y + a z · b z .

Фактически это является третьим определением скалярного произведения.

Для доказательства используем a → , b → = a → · b → · cos a → , b → ^ = a x · b x + a y · b y для векторов a → = ( a x , a y ) , b → = ( b x , b y ) на декартовой системе.

Следует отложить векторы

O A → = a → = a x , a y и O B → = b → = b x , b y .

Тогда длина вектора A B → будет равна A B → = O B → – O A → = b → – a → = ( b x – a x , b y – a y ) .

Рассмотрим треугольник O A B .

A B 2 = O A 2 + O B 2 – 2 · O A · O B · cos ( ∠ A O B ) верно , исходя из теоремы косинусов.

По условию видно, что O A = a → , O B = b → , A B = b → – a → , ∠ A O B = a → , b → ^ , значит, формулу нахождения угла между векторами запишем иначе

b → – a → 2 = a → 2 + b → 2 – 2 · a → · b → · cos ( a → , b → ^ ) .

Тогда из первого определения следует, что b → – a → 2 = a → 2 + b → 2 – 2 · ( a → , b → ) , значит ( a → , b → ) = 1 2 · ( a → 2 + b → 2 – b → – a → 2 ) .

Применив формулу вычисления длины векторов, получим:
a → , b → = 1 2 · ( ( a 2 x + a y 2 ) 2 + ( b 2 x + b y 2 ) 2 – ( ( b x – a x ) 2 + ( b y – a y ) 2 ) 2 ) = = 1 2 · ( a 2 x + a 2 y + b 2 x + b 2 y – ( b x – a x ) 2 – ( b y – a y ) 2 ) = = a x · b x + a y · b y

( a → , b → ) = a → · b → · cos ( a → , b → ^ ) = = a x · b x + a y · b y + a z · b z

– соответственно для векторов трехмерного пространства.

Скалярное произведение векторов с координатами говорит о том, что скалярный квадрат вектора равен сумме квадратов его координат в пространстве и на плоскости соответственно. a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) и ( a → , a → ) = a x 2 + a y 2 .

Скалярное произведение и его свойства

Существуют свойства скалярного произведения, которые применимы для a → , b → и c → :

1. коммутативность ( a → , b → ) = ( b → , a → ) ;
2. дистрибутивность ( a → + b → , c → ) = ( a → , c → ) + ( b → , c → ) , ( a → + b → , c → ) = ( a → , b → ) + ( a → , c → ) ;
3. сочетательное свойство ( λ · a → , b → ) = λ · ( a → , b → ) , ( a → , λ · b → ) = λ · ( a → , b → ) , λ – любое число;
4. скалярный квадрат всегда больше нуля ( a → , a → ) ≥ 0 , где ( a → , a → ) = 0 в том случае, когда a → нулевой.

Пример 1

Свойства объяснимы благодаря определению скалярного произведения на плоскости и свойствам при сложении и умножении действительных чисел.

Доказать свойство коммутативности ( a → , b → ) = ( b → , a → ) . Из определения имеем, что ( a → , b → ) = a y · b y + a y · b y и ( b → , a → ) = b x · a x + b y · a y .

По свойству коммутативности равенства a x · b x = b x · a x и a y · b y = b y · a y верны, значит a x · b x + a y · b y = b x · a x + b y · a y .

Отсюда следует, что ( a → , b → ) = ( b → , a → ) . Что и требовалось доказать.

Дистрибутивность справедлива для любых чисел:

( a ( 1 ) → + a ( 2 ) → + . . . + a ( n ) → , b → ) = ( a ( 1 ) → , b → ) + ( a ( 2 ) → , b → ) + . . . + ( a ( n ) → , b → )

и ( a → , b ( 1 ) → + b ( 2 ) → + . . . + b ( n ) → ) = ( a → , b ( 1 ) → ) + ( a → , b ( 2 ) → ) + . . . + ( a → , b → ( n ) ) ,

( a ( 1 ) → + a ( 2 ) → + . . . + a ( n ) → , b ( 1 ) → + b ( 2 ) → + . . . + b ( m ) → ) = = ( a ( 1 ) → , b ( 1 ) → ) + ( a ( 1 ) → , b ( 2 ) → ) + . . . + ( a ( 1 ) → , b ( m ) → ) + + ( a ( 2 ) → , b ( 1 ) → ) + ( a ( 2 ) → , b ( 2 ) → ) + . . . + ( a ( 2 ) → , b ( m ) → ) + . . . + + ( a ( n ) → , b ( 1 ) → ) + ( a ( n ) → , b ( 2 ) → ) + . . . + ( a ( n ) → , b ( m ) → )

Скалярное произведение с примерами и решениями

Любая задача такого плана решается с применением свойств и формул, касающихся скалярного произведения:

1. ( a → , b → ) = a → · b → · cos ( a → , b → ^ ) ;
2. ( a → , b → ) = a → · n p a → b → = b → · n p b → a → ;
3. ( a → , b → ) = a x · b x + a y · b y или ( a → , b → ) = a x · b x + a y · b y + a z · b z ;
4. ( a → , a → ) = a → 2 .

Рассмотрим некоторые примеры решения.

Длина a → равна 3, длина b → равна 7. Найти скалярное произведение, если угол имеет 60 градусов.

По условию имеем все данные, поэтому вычисляем по формуле:

( a → , b → ) = a → · b → · cos ( a → , b → ^ ) = 3 · 7 · cos 60 ° = 3 · 7 · 1 2 = 21 2

Ответ: ( a → , b → ) = 21 2 .

Заданны векторы a → = ( 1 , – 1 , 2 – 3 ) , b → = ( 0 , 2 , 2 + 3 ) . Чему равно скалярной произведение.

В данном примере рассматривается формула вычисления по координатам, так как они заданы в условии задачи:

( a → , b → ) = a x · b x + a y · b y + a z · b z = = 1 · 0 + ( – 1 ) · 2 + ( 2 + 3 ) · ( 2 + 3 ) = = 0 – 2 + ( 2 – 9 ) = – 9

Ответ: ( a → , b → ) = – 9

Найти скалярное произведение A B → и A C → . На координатной плоскости заданы точки A ( 1 , – 3 ) , B ( 5 , 4 ) , C ( 1 , 1 ) .

Для начала вычисляются координаты векторов, так как по условию даны координаты точек:

A B → = ( 5 – 1 , 4 – ( – 3 ) ) = ( 4 , 7 ) A C → = ( 1 – 1 , 1 – ( – 3 ) ) = ( 0 , 4 )

Подставив в формулу с использованием координат, получим:

( A B → , A C → ) = 4 · 0 + 7 · 4 = 0 + 28 = 28 .

Ответ: ( A B → , A C → ) = 28 .

Заданы векторы a → = 7 · m → + 3 · n → и b → = 5 · m → + 8 · n → , найти их произведение. m → равен 3 и n → равен 2 единицам, они перпендикулярные.

( a → , b → ) = ( 7 · m → + 3 · n → , 5 · m → + 8 · n → ) . Применив свойство дистрибутивности, получим:

( 7 · m → + 3 · n → , 5 · m → + 8 · n → ) = = ( 7 · m → , 5 · m → ) + ( 7 · m → , 8 · n → ) + ( 3 · n → , 5 · m → ) + ( 3 · n → , 8 · n → )

Выносим коэффициент за знак произведения и получим:

( 7 · m → , 5 · m → ) + ( 7 · m → , 8 · n → ) + ( 3 · n → , 5 · m → ) + ( 3 · n → , 8 · n → ) = = 7 · 5 · ( m → , m → ) + 7 · 8 · ( m → , n → ) + 3 · 5 · ( n → , m → ) + 3 · 8 · ( n → , n → ) = = 35 · ( m → , m → ) + 56 · ( m → , n → ) + 15 · ( n → , m → ) + 24 · ( n → , n → )

По свойству коммутативности преобразуем:

35 · ( m → , m → ) + 56 · ( m → , n → ) + 15 · ( n → , m → ) + 24 · ( n → , n → ) = = 35 · ( m → , m → ) + 56 · ( m → , n → ) + 15 · ( m → , n → ) + 24 · ( n → , n → ) = = 35 · ( m → , m → ) + 71 · ( m → , n → ) + 24 · ( n → , n → )

В итоге получим:

( a → , b → ) = 35 · ( m → , m → ) + 71 · ( m → , n → ) + 24 · ( n → , n → ) .

Теперь применим формулу для скалярного произведения с заданным по условию углом:

( a → , b → ) = 35 · ( m → , m → ) + 71 · ( m → , n → ) + 24 · ( n → , n → ) = = 35 · m → 2 + 71 · m → · n → · cos ( m → , n → ^ ) + 24 · n → 2 = = 35 · 3 2 + 71 · 3 · 2 · cos π 2 + 24 · 2 2 = 411 .

Ответ: ( a → , b → ) = 411

Если имеется числовая проекция.

Найти скалярное произведение a → и b → . Вектор a → имеет координаты a → = ( 9 , 3 , – 3 ) , проекция b → с координатами ( – 3 , – 1 , 1 ) .

По условию векторы a → и проекция b → противоположно направленные, потому что a → = – 1 3 · n p a → b → → , значит проекция b → соответствует длине n p a → b → → , при чем со знаком «-»:

n p a → b → → = – n p a → b → → = – ( – 3 ) 2 + ( – 1 ) 2 + 1 2 = – 11 ,

Подставив в формулу, получим выражение:

( a → , b → ) = a → · n p a → b → → = 9 2 + 3 2 + ( – 3 ) 2 · ( – 11 ) = – 33 .

Ответ: ( a → , b → ) = – 33 .

Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию.

Какое значение должна принять λ при заданном скалярном произведении a → = ( 1 , 0 , λ + 1 ) и b → = ( λ , 1 , λ ) будет равным -1.

Из формулы видно, что необходимо найти сумму произведений координат:

( a → , b → ) = 1 · λ + 0 · 1 + ( λ + 1 ) · λ = λ 2 + 2 · λ .

В дано имеем ( a → , b → ) = – 1 .

Чтобы найти λ , вычисляем уравнение:

λ 2 + 2 · λ = – 1 , отсюда λ = – 1 .

Физический смысл скалярного произведения

Механика рассматривает приложение скалярного произведения.

При работе А с постоянной силой F → перемещаемое тело из точки M в N можно найти произведение длин векторов F → и M N → с косинусом угла между ними, значит работа равна произведению векторов силы и перемещения:

Перемещение материальной точки на 3 метра под действием силы равной 5 ньтонов направлено под углом 45 градусов относительно оси. Найти A .

Так как работа – это произведение вектора силы на перемещение, значит, исходя из условия F → = 5 , S → = 3 , ( F → , S → ^ ) = 45 ° , получим A = ( F → , S → ) = F → · S → · cos ( F → , S → ^ ) = 5 · 3 · cos ( 45 ° ) = 15 2 2 .

Ответ: A = 15 2 2 .

Материальная точка, перемещаясь из M ( 2 , – 1 , – 3 ) в N ( 5 , 3 λ – 2 , 4 ) под силой F → = ( 3 , 1 , 2 ) , совершила работа равную 13 Дж. Вычислить длину перемещения.

При заданных координатах вектора M N → имеем M N → = ( 5 – 2 , 3 λ – 2 – ( – 1 ) , 4 – ( – 3 ) ) = ( 3 , 3 λ – 1 , 7 ) .

По формуле нахождения работы с векторами F → = ( 3 , 1 , 2 ) и M N → = ( 3 , 3 λ – 1 , 7 ) получим A = ( F ⇒ , M N → ) = 3 · 3 + 1 · ( 3 λ – 1 ) + 2 · 7 = 22 + 3 λ .

По условию дано, что A = 13 Д ж , значит 22 + 3 λ = 13 . Отсюда следует λ = – 3 , значит и M N → = ( 3 , 3 λ – 1 , 7 ) = ( 3 , – 10 , 7 ) .

Чтобы найти длину перемещения M N → , применим формулу и подставим значения:

Инструменты пользователя

Инструменты сайта

Содержание

Определение

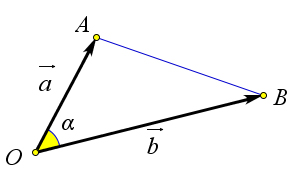
Углом между двумя ненулевыми векторами называется величина образуемого ими угла, когда они отложены от одной точки.

Определение

Скалярным произведением двух векторов называется произведение их модулей и косинуса угла между ними. Если хотя бы один из векторов нулевой, то их скалярное произведение полагают равным нулю.

Определение

Скалярным квадратом вектора называется его произведение самого на себя.

Теорема

Для любых двух ненулевых векторов их скалярное произведение равно нулю тогда и только тогда, когда они перпендикулярны.

Доказательство

А значит, $alpha=90^circ$.

Скалярное произведение в координатах

Скалярное произведение двух векторов равно сумме произведений их соответствующих координат.

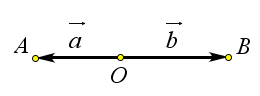
Доказательство

Рассмотрим случай, когда векторы $vec$ и $vec$ ненулевые.

Отложим от произвольной точки $O$ векторы $overrightarrow=vec$ и $overrightarrow=vec$.

Это равенство верно и в том случае, если векторы $vec$ и $vec$ коллинеарны.

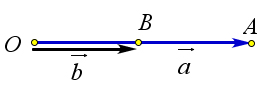
Если же $aupdownarrows b$, то $AB^2=(OA+OB)^2=OA^2+OB^2+2OAcdot OB=OA^2+OB^2-2OAcdot OBcos<180^circ>=OA^2+OB^2-2OAcdot OBcos<alpha>$.

Скалярное произведение двух векторов.

В физике работа А постоянной силы F при прямолинейном движении материальной точки из положения В в положение С (рис. 52) вычисляется по формуле

Эта формула вектору силы F и вектору перемещения ВС ставит в соответствие скалярную величину – работу. Величину А называют скалярным произведением векторов F и (overrightarrow). Скалярное произведение может быть определено для любых двух векторов. Оно широко используется в физике и в математике.

Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Если из двух векторов хотя бы один нулевой, то скалярное произведение этих векторов принимается равным нулю.

Скалярное произведение векторов а и b обозначается а • b. Итак, по определению

Если а = b, то скалярное произведение принимает вид а • a и называется скалярным квадратом вектора а и обозначается символом a 2 . Очевидно, что a 2 = а • a = |а| 2 .

Как известно, проекция вектора b на ось, направление которой совпадает с направлением вектора а, выражается формулой

Используя формулы (1) и (2), можно записать

Таким образом, скалярное произведение двух векторов равно произведению длины одного из них и проекции второго вектора на направление первого.

По формуле (1) находим

Задача 2. Найти всевозможные скалярные произведения базисных векторов i и j прямоугольной декартовой системы координат на плоскости.

По определению скалярного произведения

Задача 3. Какой знак имеет скалярное произведение векторов а и b, если
90° 0?

Свойства скалярного произведения векторов

1. Скалярное умножение векторов обладает переместительным свойством:

Если а = 0 или b = 0, то по определению скалярного произведения а Х b = 0 и b Х а = 0, т. е. а Х b = b Х а

2. Скалярное умножение векторов обладает сочетательным свойством по отношению к умножению вектора на число:

Используя свойства (1) и (4) скалярного произведения, получаем

Теорема. Для того чтобы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю:

Необходимость. Пусть a ⊥ b. Тогда

Скалярное произведение векторов, заданных своими координатами

Пусть на плоскости имеется некоторая прямоугольная декартова система координат и пусть заданы векторы а = (x₁ ; y₁ ) и b = (x₂ ; y₂). Так как

то, используя соответствующие свойства скалярного умножения векторов, получаем

Пусть теперь в пространстве имеется некоторая прямоугольная декартова система координат и заданы векторы

Аналогично предыдущему получим

Итак, скалярное произведение двух векторов равно сумме произведений одноименных координат этих векторов.

Задача 3. Найти длину вектора а = (х; у; z).

Применяя формулу (2) при b = a, получим

С другой стороны, согласно определению скалярного произведения получаем