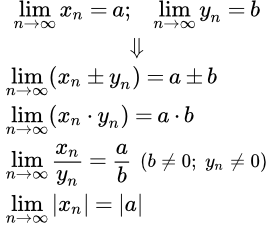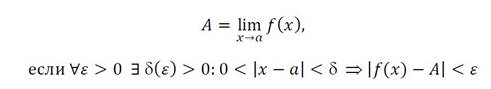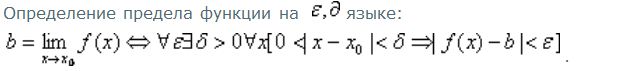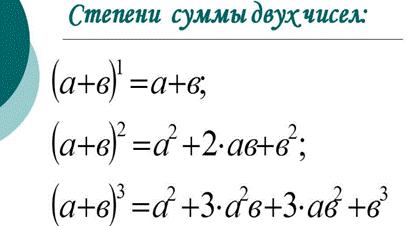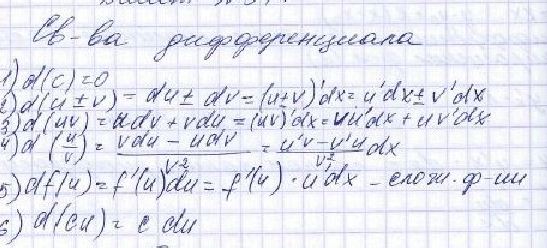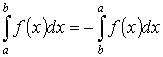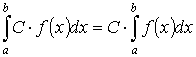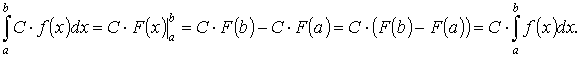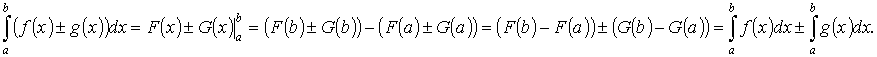Доказательство арифметических свойств пределов последовательности

Формулировки арифметических свойств

Пусть существуют конечные пределы и числовых последовательностей < x_n > и < y_n > . Тогда существуют пределы суммы, разности и произведения последовательностей, которые равны, соответственно, сумме, разности и произведению их пределов. Если b ≠ 0 и y_n ≠ 0 для всех n , то существует предел частного последовательностей, равный частному пределов:
(1) ; Доказательство ⇓
(2) ; Доказательство ⇓
(3) , если и ; Доказательство ⇓
(4) . Доказательство ⇓
Здесь C – постоянная, то есть заданное число.

Формулировки всех определений, теорем и свойств сходящихся последовательностей собраны на странице
Предел последовательности – основные теоремы и свойства.

Доказательство арифметических свойств

При доказательстве свойств, мы будем использовать определение предела последовательности:
.

Поскольку существует предел , то имеется функция такая, что для любого положительного числа ε ₁ выполняется неравенство:
(5) при .

Поскольку существует предел , то имеется функция такая, что для любого положительного числа ε ₂ выполняется неравенство:
(6) при .

Теорема о пределе суммы и разности числовых последовательностей

Все формулировки ⇑ Пусть существуют конечные пределы и последовательностей и . Тогда существуют пределы суммы и разности последовательностей < x_n ± y_n > , и они равны сумме и разности их пределов:
(1) .

Чтобы доказать свойство суммы и разности (1), нам нужно найти такую функцию , при которой, для любого положительного числа , выполняется неравенство:
(1.1) при .
При этом мы имеем функции и , при которых выполняются неравенства (5) и (6), для любых положительных и .

Воспользуемся известным неравенством
.
Преобразуем модуль разности в (1.1) и применим (5) и (6):
.
Последнее неравенство справедливо при и . Положим . Тогда, при и ,
.
Пусть, при заданном ε , есть наибольшее из чисел и . Тогда
при .

То есть мы нашли такую функцию , при которой, для любого положительного числа , выполняется неравенство:
(1.1) при .
Это и означает, что число a ± b является пределом последовательности .
Свойство доказано.

Теорема о пределе произведения числовых последовательностей

Все формулировки ⇑ Пусть существуют конечные пределы и числовых последовательностей и . Тогда существует предел произведения последовательностей < x_n· y_n > , и он равен произведению их пределов:
(2) .

Для доказательства свойства произведения (2), нам нужно найти такую функцию , при которой, для любого положительного числа , выполняется неравенство
(2.1) при .
При этом мы имеем функции и , при которых, для любых положительных и , выполняются неравенства (5) и (6):
(5) при ;
(6) при .

Преобразуем модуль разности в (2.1), применяя свойства неравенств:

.
Поскольку последовательность имеет конечный предел, то она ограничена некоторым положительным числом M_y : (см. Основные свойства пределов последовательностей). Применим (5) и (6). Тогда
.
Положим . Тогда при и ,
.
Пусть, при заданном ε , есть наибольшее из чисел и . Тогда
при .

То есть мы нашли такую функцию , при которой, для любого положительного числа , выполняется неравенство:
(2.1) при .
Это и означает, что число является пределом последовательности .
Свойство доказано.

Теорема о вынесении постоянной за знак предела

Все формулировки ⇑ Пусть существует конечный предел числовой последовательности . И пусть последовательность образована из , умножением ее на постоянное число C . Тогда постоянную C можно выносить за знак предела:
(4) .

Это свойство является следствием свойства произведения последовательностей. Для доказательства рассмотрим последовательность, все элементы которой равны числу C : . Предел этой последовательности равен этому числу:

(см. Основные свойства пределов последовательностей).

Применим свойство произведения последовательностей:
.
Свойство доказано.

Теорема о пределе частного числовых последовательностей

Все формулировки ⇑ Пусть существуют конечные пределы и числовых последовательностей и . Причем и для всех n . Тогда существует предел частного последовательностей < x_n / y > , и он равен частному их пределов:
(3) .

Для доказательства свойства частного (3), нам нужно найти такую функцию , при которой, для любого положительного , выполняется неравенство:
(3.1) при .
При этом мы имеем функции и , при которых, для любых положительных и , выполняются неравенства (5) и (6):
(5) при ;
(6) при .

Преобразуем модуль разности в (3.1), применяя свойства неравенств:

.
Тем самым мы получили следующую оценку:
(3.2) .

Сделаем оценку для . Подставим в (6) :
при .
Заметим, что есть расстояние между точками и на числовой прямой. Поскольку расстояние между точками и равно а расстояние между точками и меньше : , то расстояние между точками и больше :
, или
.
Это неравенство можно получить и другим способом. Применяя свойства неравенств и соотношение имеем:
;
;
.
Итак, мы нашли, что
при ,
где . Тогда
(3.3) при .

Подставим (5), (6) и (3.3) в (3.2):
.
Это неравенство выполняется при одновременном выполнении трех неравенств:
.
Подставим , . И пусть обозначает максимальное из чисел . Тогда
.

То есть мы нашли такую функцию
,
при которой, для любого положительного , выполняется неравенство
(3.1) при .
Это и означает, что число a/b является пределом последовательности .
Свойство доказано.

Теорема о пределе абсолютного значения элементов последовательности

Все формулировки ⇑ Пусть существует конечный предел числовой последовательности . И пусть последовательность составлена из элементов , взятых по абсолютной величине. Тогда
.

Для доказательства этого свойства, нам нужно найти такую функцию , при которой, для любого положительного , выполняется неравенство:
при .
При этом у нас есть функция , при которой выполняется неравенство (5):
(5) при .

Воспользуемся известным неравенством:

и применим (5):
.
Последнее выполняется при .
То есть мы можем взять .

Итак, для любого ,
при .
Свойство доказано.

Автор: Олег Одинцов . Опубликовано: 03-08-2017

Теоремы об арифметических свойствах пределов последовательностей.

Имеют место следующие арифметические свойства пределов вещественных последовательностей:

Признаки существования предела последовательности

1Теорема (признак существования предела). Теорема Вейерштрасса Если последовательность монотонна и ограничена, то она имеет предел.

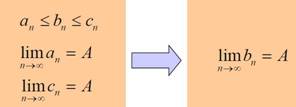
2Теорема (признак существования предела).или теорема о двух милиционерах. Если одна

последовательность заключена между двумя другими, имеющими одинаковый предел, то она имеет тот же предел.

3Критерий Коши:Для существования предела последовательности 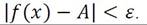, необходимо и достаточно, чтобы для любого эпсилон>0 существовало N=N(эпсилон) такое, что для всех n>N и p>0, |Xn-X(n+p)| 0, найдется такое число δ > 0 (зависящее от ε), что для всех x из δ-окрестности точки a, выполнено неравенство: Это определение называется определением на языке ε и δ,предложено французским математиком Огюстеном Коши и используется с начала XIX века по настоящее время, поскольку обладает необходимой математической строгостью и точностью.

Запишем на языке кванторов определение предела функции в точке:

25. определение предела функции на языке

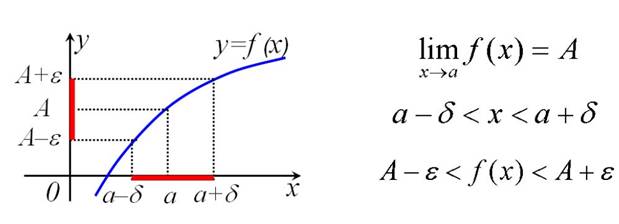
Геометрический смысл предела функции в точке

Выясним, в чем заключается геометрический смысл предела функции

в точке. Построим график функции y=f(x) и отметим на нем точки

Предел функции y=f(x) в точке x стремящееся к а существует и равен A, если

для любой ε-окрестности точки A можно указать такую δ-окрестность точки

a, что для любого x из этой δ-окрестности значение f(x) будет находиться в

ε-окрестности точки A.

Отметим, что по определению предела функции в точке для

существования предела при x → a не важно, какое значение принимает

функция в самой точке a. Можно привести примеры, когда функция не

определена при x=a или принимает значение, отличное от A. Тем не

менее, предел может быть равен A.

Свойства функций имеющих предел

Односторонние пределы функции в точке

Производная как скорость изменения функции

Производная сложной функции

Бином Ньютона

Свойства дифференциала

Таблица дифференциалов

Формула Ньютона—Лейбница

.

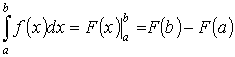
66.

1.Определённый интеграл численно равен площади криволинейной трапеции, ограниченной графиком функции у = f (x), осью абсцисс, и прямыми х = а, х = b.

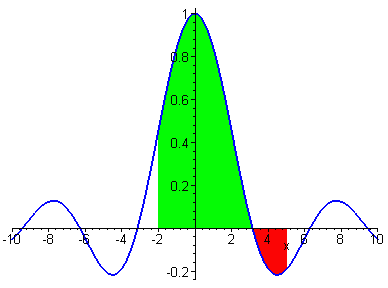
2. Если нижний и верхний пределы интегрирования поменять местами, то значение определённого интеграла изменится на противоположное

.

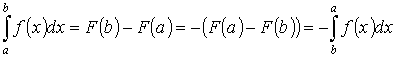
3. Если промежуток интегрирования стянут в точку, фигура под кривой стягивается в отрезок, площадь которого равна нулю

.

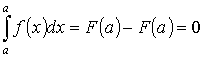
4. Постоянный множитель можно выносить за знак интеграла

,

гдеС — некоторое число.
Доказательство.

5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:

,

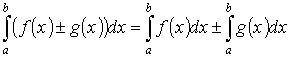
Это свойство остается справедливым для любого конечного числа слагаемых.
Доказательство.

6. Если промежуток интегрирования разбит на части, то интеграл по всему отрезку равен сумме интегралов по каждой части.

.

.

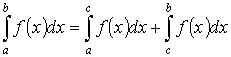
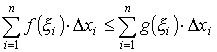
Переходя к пределу при max Δ x_i → 0, получим рассматриваемое неравенство для интегралов.
Следствие. Пусть на отрезке [a, b] гдеа

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Свойства пределов, связанные с алгебраическими операциями

Если функции и имеют конечные пределы в точке , причем и то:

Доказательство
Так как функции и имеют предел в точке , то при величины и будут бесконечно малыми. Отсюда, согласно свойствам бесконечно малых также будет бесконечно малой величиной. Что в свою очередь означает, что

Доказательство
Так как функции и имеют предел в точке , то при величины и будут бесконечно малыми. Поэтому и . Отсюда

Согласно свойствам бесконечно малых, величина в правой части — бесконечно малая. Что в свою очередь означает, что

Доказательство
Условие эквивалентно тому, что разность
бесконечно малая величина при . Покажем, что это утверждение имеет место. Приведем к общему знаменателю, получим . Рассмотрим предел числителя дроби.

Что в свою очередь означает, что

Свойства пределов, связанные с неравенствами

1. Теорема о двух милиционерах

Если 0:forall xin dot_<delta >(a)" title="exists delta > 0:forall xin dot_<delta >(a)" /> выполняются неравенства и если то .
Доказательство
Воспользуемся определением предела по Гейне. Пусть — последовательность из , причем . Тогда выполняются условия и . Тогда в силу свойств пределов последовательностей . Следовательно .
Теорему можно проиллюстрировать следующим графиком:

Если 0:forall xin dot_<delta >(a)" title="existsdelta >0:forall xin dot_<delta >(a)" /> выполняется неравенство и если , , то .

Доказательство
Воспользуемся определением предела по Гейне. Пусть — последовательность из , тогда числа и будут пределами последовательности т.е. и Тогда в силу свойств пределов последовательностей .