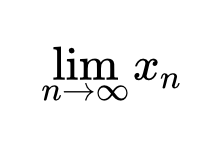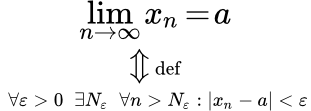Доказательство существования предела последовательности

Определение последовательности

Более подробно см. страницу Определение числовой последовательности >>>.
Далее мы будем считать, что элементами последовательности являются действительные числа.

Последовательность называется ограниченной, если существует такое число M , что для всех действительных n .
Верхней гранью последовательности называют наименьшее из чисел, ограничивающее последовательность сверху. То есть это такое число s , для которого для всех n и для любого , найдется такой элемент последовательности , превосходящий s′ : .
Нижней гранью последовательности называют наибольшее из чисел, ограничивающее последовательность снизу. То есть это такое число i , для которого для всех n и для любого , найдется такой элемент последовательности , меньший i′ : .

Верхнюю грань также называют точной верхней границей, а нижнюю грань – точной нижней границей. Понятия верхней и нижней граней справедливы не только к последовательностям, но и к любым множествам действительных чисел.

Определение предела последовательности

С помощью логических символов существования и всеобщности определение предела можно записать следующим образом:
.

ε – окрестность точки a – это открытый интервал ( a – ε, a + ε ) . Сходящаяся последовательность – это последовательность, у которой существует предел .
Также говорят, что последовательность сходится к a . Расходящаяся последовательность – это последовательность, не имеющая предела.

Точка a не является пределом последовательности , если существует такое , что для любого натурального n существует такое натуральное m > n , что
.
.
Это означает, что можно выбрать такую ε – окрестностью точки a , за пределами которой будет находиться бесконечное число элементов последовательности.

Свойства конечных пределов последовательностей

Основные свойства

Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.

Если число a не является пределом последовательности , то существует такая окрестность точки a , за пределами которой находится бесконечное число элементов последовательности.

Теорема единственности предела числовой последовательности. Если последовательность имеет предел, то он единственный.

Если последовательность имеет конечный предел, то она ограничена.

Если каждый элемент последовательности равен одному и тому же числу C : , то эта последовательность имеет предел, равный числу C .

Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.

Арифметические действия с пределами

Пусть существуют конечные пределы и последовательностей и . И пусть C – постоянная, то есть заданное число. Тогда
;
;
;
, если .
В случае частного предполагается, что для всех n .

Свойства, связанные с неравенствами

Если и элементы последовательности, начиная с некоторого номера, удовлетворяют неравенству , то и предел a этой последовательности удовлетворяет неравенству .

Если и элементы последовательности, начиная с некоторого номера, принадлежат замкнутому интервалу (сегменту) , то и предел a также принадлежит этому интервалу: .

Если и и элементы последовательностей, начиная с некоторого номера, удовлетворяют неравенству , то .

Если и, начиная с некоторого номера, , то .
В частности, если, начиная с некоторого номера, , то
если , то ;
если , то .

Пусть и . Если a b , то найдется такое натуральное число N , что для всех n > N выполняется неравенство .

Бесконечно большая и бесконечно малая последовательности

Бесконечно малая последовательность

Сумма и разность конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

Произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.

Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

Для того, чтобы последовательность имела предел a , необходимо и достаточно, чтобы , где – бесконечно малая последовательность.

Доказательства свойств бесконечно малых последовательностей приведены на странице
Бесконечно малые последовательности – определение и свойства >>>.

Бесконечно большая последовательность

Бесконечно большая последовательность – это последовательность, имеющая бесконечно большой предел. То есть если для любого положительного числа существует такое натуральное число N , зависящее от , что для всех натуральных выполняется неравенство
.
В этом случае пишут
.
Или при .
Говорят, что стремится к бесконечности.

Если , начиная с некоторого номера N , то
.
Если же , то
.

Если последовательность являются бесконечно большой, то, начиная с некоторого номера N , определена последовательность , которая является бесконечно малой. Если являются бесконечно малой последовательностью с отличными от нуля элементами, то последовательность является бесконечно большой.

Если последовательность бесконечно большая, а последовательность ограничена, то
.

Если абсолютные значения элементов последовательности ограничены снизу положительным числом ( ), а – бесконечно малая с неравными нулю элементами, то
.

Более подробно определение бесконечно большой последовательности с примерами приводится на странице
Определение бесконечно большой последовательности >>>.
Доказательства свойств бесконечно больших последовательностей приведены на странице
Свойства бесконечно больших последовательностей >>>.

Критерии сходимости последовательностей

Монотонные последовательности

Аналогичными неравенствами определяются другие монотонные последовательности.

Строго убывающая последовательность:
.
Неубывающая последовательность:
.
Невозрастающая последовательность:
.

Отсюда следует, что строго возрастающая последовательность также является неубывающей. Строго убывающая последовательность также является невозрастающей.

Монотонная последовательность – это неубывающая или невозрастающая последовательность.

Монотонная последовательность ограничена, по крайней мере, с одной стороны значением . Неубывающая последовательность ограничена снизу: . Невозрастающая последовательность ограничена сверху: .

Теорема Вейерштрасса. Для того чтобы неубывающая (невозрастающая) последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной сверху (снизу ). Здесь M – некоторое число.

Поскольку любая неубывающая (невозрастающая) последовательность ограничена снизу (сверху), то теорему Вейерштрасса можно перефразировать следующим образом:

Для того чтобы монотонная последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной: .

Монотонная неограниченная последовательность имеет бесконечный предел, равный для неубывающей и для невозрастающей последовательности.

Критерий Коши сходимости последовательности

Условие Коши
Последовательность удовлетворяет условию Коши, если для любого существует такое натуральное число , что для всех натуральных чисел n и m , удовлетворяющих условию , выполняется неравенство
.

Фундаментальная последовательность – это последовательность, удовлетворяющая условию Коши.

Критерий Коши сходимости последовательности. Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она удовлетворяла условию Коши.

Доказательство критерия сходимости Коши приведено на странице
Критерий Коши сходимости последовательности >>>.

Подпоследовательности

Теорема Больцано – Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность. А из любой неограниченной последовательности – бесконечно большую подпоследовательность, сходящуюся к или к .

Доказательство теоремы Больцано – Вейерштрасса приведено на странице
Теорема Больцано – Вейерштрасса >>>.

Определения, теоремы и свойства подпоследовательностей и частичных пределов рассмотрены на странице
Подпоследовательности и частичные пределы после­довательностей>>>.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
В.А. Зорич. Математический анализ. Часть 1. Москва, 1997.
В.А. Ильин, Э.Г. Позняк. Основы математического анализа. Часть 1. Москва, 2005.

Автор: Олег Одинцов . Опубликовано: 09-07-2017 Изменено: 30-12-2018

Здесь мы рассмотрим определение конечного предела последовательности. Случай последовательности, сходящейся к бесконечности, рассмотрен на странице «Определение бесконечно большой последовательности».

Определение предела последовательности

ε – окрестность точки a – это открытый интервал ( a – ε, a + ε ). Сходящаяся последовательность – это последовательность, у которой существует предел . Также говорят, что последовательность сходится к a . Расходящаяся последовательность – это последовательность, не имеющая предела.

Из определения следует, что, если последовательность имеет предел a , то какую бы ε – окрестностью точки a мы не выбрали, за ее пределами может оказаться, лишь конечное число элементов последовательности, или вообще ни одного (пустое множество). А любая ε – окрестность содержит бесконечное число элементов. В самом деле, задав определенное число ε , мы, тем самым имеем число . Так что все элементы последовательности с номерами , по определению, находятся в ε – окрестностью точки a . Первые элементов могут находиться где угодно. То есть за пределами ε – окрестности может находиться не более элементов – то есть конечное число.

Также заметим, что разность вовсе не обязана монотонно стремиться к нулю, то есть все время убывать. Она может стремиться к нулю не монотонно: может то возрастать, то убывать, имея локальные максимумы. Однако эти максимумы, с ростом n , должны стремиться к нулю (возможно тоже не монотонно).

С помощью логических символов существования и всеобщности, определение предела можно записать следующим образом:
(1) .

Определение, что число a не является пределом

Теперь рассмотрим обратное утверждение, что число a не является пределом последовательности.

Число a не является пределом последовательности , если существует такое , что для любого натурального n существует такое натуральное m > n , что
.

Запишем это утверждение с помощью логических символов.
(2) .

Утверждение, что число a не является пределом последовательности, означает, что
можно выбрать такую ε – окрестность точки a , за пределами которой будет находиться бесконечное число элементов последовательности.

Рассмотрим пример. Пусть задана последовательность с общим элементом
(3)
Любая окрестность точки содержит бесконечное число элементов. Однако эта точка не является пределом последовательности, поскольку и любая окрестность точки также содержит бесконечное число элементов. Возьмем ε – окрестность точки с ε = 1 . Это будет интервал ( –1, +1) . Все элементы, кроме первого, с четными n принадлежат этому интервалу. Но все элементы с нечетными n находятся за пределами этого интервала, поскольку они удовлетворяют неравенству x_n > 2 . Поскольку число нечетных элементов бесконечно, то за пределами выбранной окрестности будет находиться бесконечное число элементов. Поэтому точка не является пределом последовательности.

Теперь покажем это, строго придерживаясь утверждения (2). Точка не является пределом последовательности (3), поскольку существует такое , так что, для любого натурального n , существует нечетное , для которого выполняется неравенство
.

Также можно показать, что любая точка a не может являться пределом этой последовательности. Мы всегда можем выбрать такую ε – окрестность точки a , которая не содержит либо точку 0, либо точку 2. И тогда за пределами выбранной окрестности будет находиться бесконечное число элементов последовательности.

Эквивалентное определение предела последовательности

Можно дать эквивалентное определение предела последовательности, если расширить понятие ε – окрестности. Мы получим равносильное определение, если в нем, вместо ε – окрестности, будет фигурировать любая окрестность точки a . Окрестности точки – это любой открытый интервал, содержащий эту точку. Математически окрестность точки определяется так: , где ε ₁ и ε ₂ – произвольные положительные числа.

Тогда эквивалентное определение предела будет следующим.

Предел последовательности – это такое число a , если для любой его окрестности существует такое натуральное число N , так что все элементы последовательности с номерами принадлежат этой окрестности.

Это определение можно представить и в развернутом виде.

Предел последовательности – это такое число a , если для любых положительных чисел и существует такое натуральное число N , зависящее от и , что для всех натуральных выполняются неравенства
.

Доказательство равносильности определений

Докажем, что, представленные выше, два определения предела последовательности равносильны.

Пусть число a является пределом последовательности согласно первому определению. Это означает, что имеется функция , так что для любого положительного числа ε выполняются неравенства:
(4) при .

Покажем, что число a является пределом последовательности и по второму определению. То есть нам нужно показать, что существует такая функция , так что для любых положительных чисел ε ₁ и ε ₂ выполняются неравенства:
(5) при .

Пусть мы имеем два положительных числа: ε ₁ и ε ₂ . И пусть ε – наименьшее из них: . Тогда ; ; . Используем это в (5):
.
Но неравенства выполняются при . Тогда и неравенства (5) выполняются при .

То есть мы нашли такую функцию , при которой выполняются неравенства (5) для любых положительных чисел ε ₁ и ε ₂ .
Первая часть доказана.

Теперь пусть число a является пределом последовательности согласно второму определению. Это означает, что имеется функция , так что для любых положительных чисел ε ₁ и ε ₂ выполняются неравенства:
(5) при .

Покажем, что число a является пределом последовательности и по первому определению. Для этого нужно положить . Тогда при выполняются неравенства:
.
Это соответствует первому определению с .
Равносильность определений доказана.

Примеры

Все примеры Здесь мы рассмотрим несколько примеров, в которых требуется доказать, что заданное число a является пределом последовательности. При этом нужно задать произвольные положительное число ε и определить функцию N от ε такую, что для всех выполняется неравенство .

Пример 1

Выпишем определение предела последовательности:
(1) .
В нашем случае ;
.

Вводим положительные числа и :
.
Воспользуемся свойствами неравенств. Тогда если и , то
.

То есть, для любого положительного , мы можем взять любое натуральное число, большее или равное :
.
Тогда
при .
Это означает, что число является пределом заданной последовательности:
.

Пример 2

Все примеры ⇑ С помощью определения предела последовательности доказать, что
.

Выпишем определение предела последовательности:
(1) .
В нашем случае , ;
.

Вводим положительные числа и :
.
Воспользуемся свойствами неравенств. Тогда если и , то
.

То есть, для любого положительного , мы можем взять любое натуральное число, большее или равное :
.
Тогда
при .
Это означает, что число является пределом последовательности :
.

Пример 3

Все примеры ⇑ Используя определение предела последовательности доказать, что
.

Вводим обозначения , .
Преобразуем разность:
.
Для натуральных n = 1, 2, 3, . имеем:
.

Выпишем определение предела последовательности:
(1) .
Вводим положительные числа и :
.
Тогда если и , то
.

То есть, для любого положительного , мы можем взять любое натуральное число, большее или равное :
.
При этом
при .
Это означает, что число является пределом последовательности :
.

Пример 4

Все примеры ⇑ Используя определение предела последовательности доказать, что
.

Выпишем определение предела последовательности:
(1) .
В нашем случае , ;
.

Вводим положительные числа и :
.
Тогда если и , то
.

То есть, для любого положительного , мы можем взять любое натуральное число, большее или равное :
.
Тогда
при .
Это означает, что число является пределом последовательности :
.

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов . Опубликовано: 12-07-2017 Изменено: 08-12-2017

Определение пределов последовательности и функции, свойства пределов, первый и второй замечательные пределы, примеры.

Постоянное число а называется пределом последовательности _n>, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения x_n, у которых n>N, удовлетворяют неравенству

|x_n – a| N, лежат внутри интервала (a-ε , a+ε), т.е. попадают в какую угодно малую ε-окрестность точки а.

Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.

Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции x_n = f(n) целочисленного аргумента n.

Пусть дана функция f(x) и пусть a – предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка a может принадлежать множеству D(f), а может и не принадлежать ему.

Определение 1. Постоянное число А называется предел функции f(x) при x→ a, если для всякой последовательности _n> значений аргумента, стремящейся к а, соответствующие им последовательности _n)> имеют один и тот же предел А.

Это определение называют определением предела функции по Гейне, или “на языке последовательностей”.

Определение 2. Постоянное число А называется предел функции f(x) при x→a, если, задав произвольное, как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех x, лежащих в ε-окрестности числа а, т.е. для x, удовлетворяющих неравенству
0 » 2.7 – основание натурального логарифма. Формулы (6.10) и (6.11) носят название первый замечательного предело и второй замечательный предел.

Используются на практике и следствия формулы (6.11):

(6.12)

(6.13)

(6.14)

в частности предел,

Eсли x → a и при этом x > a, то пишут x →a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а. Чтобы существовал предел функции f(x) при x→ a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x, если предел

(6.15)

Условие (6.15) можно переписать в виде:

то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.

Если равенство (6.15) нарушено, то говорят, что при x = x_o функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R, кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x_o)= f(0) не определено, поэтому в точке x_o = 0 функция имеет разрыв.

Функция f(x) называется непрерывной справа в точке x_o, если предел

и непрерывной слева в точке x_o, если предел

Непрерывность функции в точке x_o равносильна ее непрерывности в этой точке одновременно и справа и слева.

Для того, чтобы функция была непрерывна в точке x_o, например, справа, необходимо, во-первых, чтобы существовал конечный предел , а во-вторых, чтобы этот предел был равен f(x_o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.

1. Если предел существует и не равен f(x_o), то говорят, что функция f(x) в точке x_o имеет разрыв первого рода, или скачок.

2. Если предел равен +∞ или -∞ или не существует, то говорят, что в точке x_o функция имеет разрыв второго рода.

Например, функция y = ctg x при x → +0 имеет предел, равный +∞ , значит, в точке x=0 она имеет разрыв второго рода. Функция y = E(x) (целая часть от x) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.

Функция, непрерывная в каждой точке промежутка [a,b], называется непрерывной в [a,b]. Непрерывная функция изображается сплошной кривой.

Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.

Рассмотрим пример Я. И. Перельмана, дающий интерпретацию числа e в задаче о сложных процентах. Число e есть предел . В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода – в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:

100×(1 +1/10) 10 ≈ 259 (ден. ед.),

100×(1+1/100) 100 ≈ 270 (ден. ед.),

100×(1+1/1000) 1000 ≈271 (ден. ед.).

При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что предел

Пример 3.1. Пользуясь определением предела числовой последовательности, доказать, что последовательность x_n =(n-1)/n имеет предел, равный 1.

Решение. Нам надо доказать, что, какое бы ε > 0 мы ни взяли, для него найдется натуральное число N, такое, что для всех n > N имеет место неравенство |x_n -1| 0. Так как x_n -1 =(n+1)/n – 1= 1/n, то для отыскания N достаточно решить неравенство 1/n 1/ε и, следовательно, за N можно принять целую часть от 1/ε N = E(1/ε). Мы тем самым доказали, что предел .

Пример 3.2. Найти предел последовательности, заданной общим членом .

Решение. Применим теорему предел суммы и найдем предел каждого слагаемого. При n → ∞ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему предел частного. Поэтому сначала преобразуем x_n, разделив числитель и знаменатель первого слагаемого на n 2 , а второго на n. Затем, применяя теорему предел частного и предел суммы, найдем:

Пример 3.3. . Найти .

Решение.

Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.

Пример 3.4. Найти ().

Решение. Применять теорему предел разности нельзя, поскольку имеем неопределенность вида ∞-∞. Преобразуем формулу общего члена:

Пример 3.5. Дана функция f(x)=2 1/x . Доказать, что предел не существует.

Решение. Воспользуемся определением 1 предела функции через последовательность. Возьмем последовательность < x_n >, сходящуюся к 0, т.е. Покажем, что величина f(x_n)= для разных последовательностей ведет себя по-разному. Пусть x_n = 1/n. Очевидно, что , тогда предел Выберем теперь в качестве x_n последовательность с общим членом x_n = -1/n, также стремящуюся к нулю. Поэтому предел не существует.

Пример 3.6. Доказать, что предел не существует.

Решение. Пусть x₁, x₂. x_n. – последовательность, для которой
. Как ведет себя последовательность _n)> = n > при различных x_n→ ∞

Если x_n= p n, то sin x_n= sin ( p n) = 0 при всех n и предел Если же
x_n=2 p n+ p /2, то sin x_n= sin(2 p n+ p /2) = sin p /2 = 1 для всех n и следовательно предел . Таким образом, не существует.

Пример 3.7 Найти предел

Решение. Имеем: . Обозначим t = 5x. При x →0 имеем: t →0. Применяя формулу (3.10), получим .

Пример 3.8. Вычислить предел .

Решение. Обозначим y=π-x. Тогда при x→π, y→0. Имеем:

sin 3x = sin 3(π-y) = sin(3π-3y) = sin 3y.

sin 4x = sin 4(π-y) = sin (π4-4y)= – sin 4y.

_Предел

Пример 3.9. Найти предел .

Решение. Обозначим arcsin x=t. Тогда x=sin t и при x→0, t→0. .

Пример 3.10. Найти 1) ;

2) ;

3) .

1) Применяя теорему 1 предел разности и предел произведения, находим предел знаменателя: .

Предел знаменателя не равен нулю, поэтому, по теореме 1 предел частного, получаем:

.

2) Здесь числитель и знаменатель стремятся к нулю, т.е. имеет место неопределенность вида 0/0. Теорема о пределе частного непосредственно неприменима. Для “раскрытия неопределенности” преобразуем данную функцию. Разделив числитель и знаменатель на x-2, получим при x ≠ 2 равенство:

Так как предел , то, по теореме предел частного, найдем

3. Числитель и знаменатель при x &rarr ∞ являются бесконечно большими функциями. Поэтому теорема предел частного непосредственно не применима. Разделим числитель и знаменатель на x 2 и к полученной функции применим теорему предел частного:

.

Пример 3.11. Найти предел .

Решение. Здесь числитель и знаменатель стремятся к нулю:, x-9→0, т.е. имеем неопределенность вида .

Преобразуем данную функцию, умножив числитель и знаменатель на неполный квадрат суммы выражения , получим

.

Пример 3.12. Найти предел .

Решение.