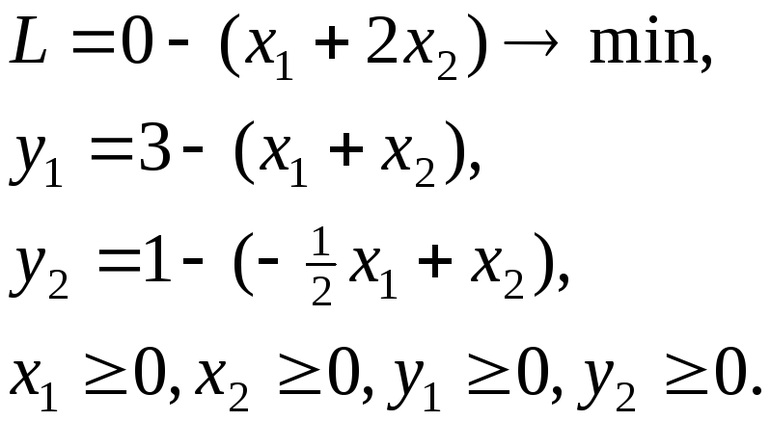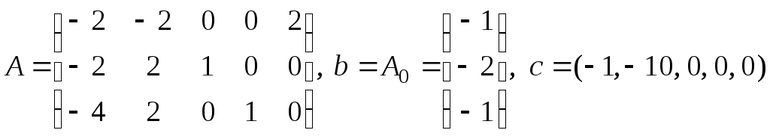Двойственный симплекс метод пример

Условие задачи

Для реализации трех групп товаров коммерческое предприятие располагает тремя видами ограниченных материально-денежных ресурсов в количестве b₁ = 240, b₂ = 200, b₃ = 160 единиц. При этом для продажи 1 группы товаров на 1 тыс. руб. товарооборота расходуется ресурса первого вида в количестве a₁₁ = 2 единицы, ресурса второго вида в количестве a₂₁ = 4 единицы, ресурса третьего вида в количестве a₃₁ = 4 единицы. Для продажи 2 и 3 групп товаров на 1 тыс. руб. товарооборота расходуется соответственно ресурса первого вида в количестве a₁₂ = 3, a₁₃ = 6 единицы, ресурса второго вида в количестве a₂₂ = 2, a₂₃ = 4 единицы, ресурса третьего вида в количестве a₃₂ = 6, a₃₃ = 8 единиц. Прибыль от продажи трех групп товаров на 1 тыс. руб. товарооборота составляет соответственно c₁ = 4, c₂ = 5, c₃ = 4 (тыс. руб.). Определить плановый объем и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.

К прямой задаче планирования товарооборота, решаемой симплекс методом, составить двойственную задачу линейного программирования.
Установить сопряженные пары переменных прямой и двойственной задачи.
Согласно сопряженным парам переменных из решения прямой задачи получить решение двойственной задачи, в которой производится оценка ресурсов, затраченных на продажу товаров.

Решение задачи симплекс методом

= 0>>><

Решаем симплекс методом.

Вводим дополнительные переменные x₄ ≥ 0, x₅ ≥ 0, x₆ ≥ 0, чтобы неравенства преобразовать в равенства.

Данные заносим в симплекс таблицу

Симплекс таблица № 1

0 · 240 + 0 · 200 + 0 · 160 = 0

Вычисляем оценки по формуле:

Δ₁ = 0 · 2 + 0 · 4 + 0 · 4 – 4 = – 4
Δ₂ = 0 · 3 + 0 · 2 + 0 · 6 – 5 = – 5
Δ₃ = 0 · 6 + 0 · 4 + 0 · 8 – 4 = – 4
Δ₄ = 0 · 1 + 0 · 0 + 0 · 0 – 0 = 0
Δ₅ = 0 · 0 + 0 · 1 + 0 · 0 – 0 = 0
Δ₆ = 0 · 0 + 0 · 0 + 0 · 1 – 0 = 0

Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:

Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x₂.

= 26.667

Наименьшее неотрицательное: Q₃ = 26.667. Выводим переменную x₆ из базиса

3-ю строку делим на 6.
Из 1-й строки вычитаем 3-ю строку, умноженную на 3
Из 2-й строки вычитаем 3-ю строку, умноженную на 2

Получаем новую таблицу:

Симплекс таблица № 2

0 · 160 + 0 · 440/3 + 5 · 80/3 = 400/3

Вычисляем оценки по формуле:

Δ₁ = 0 · 0 + 0 · 8/3 + 5 · 2/3 – 4 = – 2/3
Δ₂ = 0 · 0 + 0 · 0 + 5 · 1 – 5 = 0
Δ₃ = 0 · 2 + 0 · 4/3 + 5 · 4/3 – 4 = 8/3
Δ₄ = 0 · 1 + 0 · 0 + 5 · 0 – 0 = 0
Δ₅ = 0 · 0 + 0 · 1 + 5 · 0 – 0 = 0
Δ₆ = 0 · (–1)/2 + 0 · (–1)/3 + 5 · 1/6 – 0 = 5/6

Поскольку есть отрицательная оценка Δ₁ = – 2/3, то план не оптимален.

Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x₁.

Наименьшее неотрицательное: Q₃ = 40. Выводим переменную x₂ из базиса

3-ю строку делим на 2/3.
Из 2-й строки вычитаем 3-ю строку, умноженную на 8/3

Получаем новую таблицу:

Симплекс таблица № 3

0 · 160 + 0 · 40 + 4 · 40 = 160

Вычисляем оценки по формуле:

Δ₁ = 0 · 0 + 0 · 0 + 4 · 1 – 4 = 0
Δ₂ = 0 · 0 + 0 · (–4) + 4 · 3/2 – 5 = 1
Δ₃ = 0 · 2 + 0 · (–4) + 4 · 2 – 4 = 4
Δ₄ = 0 · 1 + 0 · 0 + 4 · 0 – 0 = 0
Δ₅ = 0 · 0 + 0 · 1 + 4 · 0 – 0 = 0
Δ₆ = 0 · (–1)/2 + 0 · (–1) + 4 · 1/4 – 0 = 1

Поскольку отрицательных оценок нет, то план оптимален.

То есть необходимо реализовать товар первого вида в объеме 40 тыс. руб. Товар 2-го и 3-го видов реализовывать не надо. При этом максимальная прибыль составит F_max = 160 тыс. руб.

Решение двойственной задачи

Двойственная задача имеет вид:

=4> <3y_1 + 2y_2 + 6y_3>=5> <6y_1 + 4y_2 + 8y_3>=4> = 0>>><

Вводим дополнительные переменные y₄ ≥ 0, y₅ ≥ 0, y₆ ≥ 0, чтобы неравенства преобразовать в равенства.

Сопряженные пары переменных прямой и двойственной задач имеют вид:

Основные	Дополнительные
x1	x2	x3	x4	x5	x6
y4	y5	y6	y1	y2	y3
Дополнительные	Основные

Из последней симплекс таблицы № 3 прямой задачи, находим решение двойственной задачи:

Автор: Олег Одинцов . Опубликовано: 08-12-2011

Метод, при котором вначале симплекс-методом решается одна из взаимно двойственных задач, а затем оптимум и оптимальное решение другой задачи находятся с помощью теорем двойственности, называется двойственным симплекс-методом.

Теорема 1 (Первая теорема двойственности). Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и

другая, причем оптимальные значения их целевых функций равны:

. (7.1)

Если целевая функция исходной задачи не ограничена, то система ограничений двойственной задачи несовместна.

Примечание: утверждение, обратное по отношению ко второй части первой теоремы двойственности, в общем случае неверно.

Установим соответствие между переменными взаимно двойственных задач.

Теорема 2. Компоненты оптимального плана двойственной задачи (обладающие условием неотрицательности) равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.

Компоненты оптимального плана двойственной задачи (не ограниченные по знаку) равны значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.

Теорема 3. Положительным (ненулевым) компонентам оптимального решения одной из задач симметричной двойственной пары соответствуют нулевые компоненты оптимального решения другой задачи, т.е. для любых и :

Теорема 4 (Третья теорема двойственности). Компоненты оптимального плана двойственной задачи равны значениям частных производных линейной функции по соответствующим аргументам, т.е.

. (7.2)

Экономическая интерпретация третьей теоремы двойственности: компоненты оптимального плана двойственной задачи показывают, на сколько денежных единиц изменится максимальная прибыль (выручка) от реализации продукции при изменении запаса соответствующего ресурса на одну единицу.

Пример 9.1. На основе решения примера 5.2 (файл «Алгоритм и примеры симплекс-метода») определим двойственным симплекс- методом оптимальное решение двойственной задачи.

Исходная задача

Двойственная задача

Данная двойственная пара является симметричной. Задачи записаны в стандартной форме, приведем их к каноническому виду:

Исходная задача

Двойственная задача

Установим соответствие между переменными взаимно двойственных задач.

На основе решения примера 5.2. симплекс-таблица последней итерации (таблица 5.10) имеет вид:

Таблица 9.3

Симплекс-таблица оптимального решения исходной задачи

В соответствии с теоремой 2, оптимальные значения переменных и будут равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.

По таблице 9.3 выпишем целевую функцию исходной задачи, выраженную через свободные переменные ее оптимального решения:

.

Следовательно, , .

Переменные , , и не присутствуют в целевой функции (т.е. коэффициенты при них равны нулю), следовательно, оптимальные значения соответствующих им переменных , , и равны нулю.

В соответствии с теоремой 1, .

Таким образом, оптимальное значение целевой функции , которое достигается при .

Ответ: , .

Пример 9.2. На основе решения исходной задачи найти оптимальное решение двойственной задачи используя двойственный симплекс-метод.

Исходная задача

Двойственная задача

Данная двойственная пара является несимметричной. Приведем к каноническому виду двойственную задачу.

Исходная задача

Двойственная задача

Для установления соответствия переменных двойственной пары введем в исходную задачу две недостающие фиктивные переменные.

Исходная задача

Двойственная задача

Установим соответствие между переменными взаимно двойственных задач.

Таблица 9.4

Соответствие переменных двойственной пары

Решим исходную задачу симплекс-методом.

Используя метод Жордана-Гаусса, выделим в системе ограничений исходной задачи в качестве базисных переменные и (примечание: не использовать в качестве базисных фиктивные переменные).

В результате преобразований получим следующую матрицу коэффициентов:

.

Система ограничений исходной задачи примет следующий вид:

Выразим базисные переменные через свободные, в результате исходная задача примет следующий вид:

Подставив полученные значения базисных переменных в целевую функцию, она примет следующий вид:

В результате решения симплекс-методом преобразованной исходной задачи на последней итерации получим следующую симплекс-таблицу:

Таблица 9.5

Симплекс-таблица оптимального решения исходной задачи

Понятие и алгоритм

Под симплексным методом понимается последовательный переход от одного базисного нахождения системы решений к другому. Эта перестановка повторяется до тех пор, пока переменная величина цели не достигнет своего наибольшего или наименьшего значения. Такой подход является универсальным, его можно использовать для решения любой задачи последовательного программирования.

Метод был разработан в 1947 году математиком из США Бернардом Данцигом. Предложенный способ оказался весьма эффективным для решения задач, связанных с оптимизацией использования ограниченных ресурсов. То есть он позволяет оценить и откорректировать параметры системы, а также получить качественные аналитические результаты.

Существует два подхода решения задачи:

Первый можно использовать для оптимизационного решения двухмерных задач. Например, существует два производственных цикла по сборке ящиков. Выпуск товара характеризуется ограничением в поставках древесины и временем формовки изделия. Для одного необходимо 30 досок, а для другого — 40. Поставщики доставляют в неделю 2 тыс. единиц материала. Первый ящик собирается за 15 минут, а второй — за 30. Нужно определить, какое количество ящиков необходимо производить за неделю на первом конвейере и на втором. При этом первое изделие приносит 10 рублей прибыли, а второе — пять. Время изготовление ограничено 160 часами.

Решение заключается в принятии за Х1 и Х2 количество выпущенных ящиков. Затем — в нахождении максимальной еженедельной прибыли и описании процесса ограничения в виде уравнения.

Это типовая двухмерная задача, условия неотрицательности которой определяются границами прямых: 30*Х1 + 4 0*Х 2 ≤ 2000 (для досок) и 20*Х 1 ≤ 50*Х 2 = 1600 (для сборки). Отложив по оси ординат Х1, а Х2 по абсцисс, и указав на них точки соответствующие уравнениям, можно будет подобрать оптимальное решение для использования сырья и времени.

Графический метод удобно применять для двухмерных задач, но его невозможно использовать при решениях, связанных с размерностью, превышающей три. При этом во всех алгоритмах оптимальный результат принимается допустимым базисному. Симплекс-метод же является вычислительной процедурой, использующей принятое положение, описываемое в алгебраической форме.

Симплекс-метод при базисном решении

Впервые способ был изложен Данцигом в книге «Линейное программирование, его обобщения и применения», изданной на русском языке в 1966 году. Эта теория основывалась на вычислительной процедуре и представлялась в виде стандартных алгебраических форм. Основное направление метода заключается в указании способа нахождения опорного решения, переходе к другому, более оптимальному расчёту и определении критериев, позволяющих остановить перебор опорных вариантов.

Алгоритм решения задачи линейного программирования симплекс методом следующий:

1. Свести поставленную задачу к канонической форме путём переноса свободных членов в правую часть и ввода дополнительных переменных. В случае отрицательных переменных неравенство умножается на -1. Если в записи используется знак «меньше или равно», переменная используется положительная, в противном случае — отрицательная.
2. В зависимости от количества вводимых значений все переменные принимаются за основные. Их необходимо выразить через неосновные и перейти к базовому решению.
3. Через неосновные переменные выражается функция цели.
4. Если при решении отыскивается ответ с максимумом или минимумом линейной формы и все неосновные переменные получаются только положительными, то задача считается выполненной.
5. Если найденный максимум (минимум) линейной формы в функции имеет одну или несколько неосновных переменных с отрицательными коэффициентами, необходимо перейти к новому базисному решению.
6. Из переменных, входящих в форму с отрицательными или положительными коэффициентами, выбирается наибольшая (по модулю) и переводится в основные.

Другими словами, указывается оптимальное опорное решение, способ перехода от одного нахождения ответа к другому, варианты улучшения расчётов. После нахождения первоначального решения с «единичным базисом» вычисляется оценка разложения векторов по базису и заполняется симплексная таблица.

В тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи, используют метод с искусственным базисом. Это симплекс-метод с так называемой М-задачей (ММЭ), решаемый способом добавления к левой части системы уравнений искусственных единичных векторов. При этом новая матрица должна содержать группу единичных линейно-независимых векторов.

Двухфазный способ

Двойственный метод используется при анализе задач линейного программирования, записанного в форме основной задачи. При этом среди векторов, m уравнений, составленных из коэффициентов, должны быть единичные. Такой метод можно использовать, когда свободные члены уравнений являются любыми числами.

Например, существует ограниченность, описываемая функцией:

F = C 1 X 1+ C 2 X 2+…+ CnXn. Используется условие, что Х1Р1+Х2Р2+…+Х(m +1) P (m +1)+ +… XnPn = Р0, где Х j больше либо равно 0 (j =1, n). Принимается, что среди чисел bi (i =1, m) имеются отрицательные.

Решением будет выражение: х= (b1; b2;…; bm ;0;…;0), однако этот ответ не будет разрешать задание, так как к нему могут относиться и отрицательные числа. Так как векторы Р1, Р2… Рм единичные, то каждый из них можно описать линейной областью, состоящей из них же. При этом коэффициентами разложения векторов Рj по области будут числа: Xij = aij (i =1, m; j =1, n) по модулю.

Выражение х= ( b1; b2;…; bm ;0;…;0) определяется базисом. Называют его псевдоплан. Считается, что если дельта j больше либо равна нулю, то для любого: j ( j =1, n ) по модулю. В то же время если в псевдоплане с находимым базисом существует хотя бы одно отрицательное число, то тогда задача вообще не будет иметь планов. Но когда для этих отрицательных чисел верно, что аij меньше нуля, то можно будет перейти к новому псевдоплану.

Объяснение псевдоплана помогает построить алгоритм двойственного метода. Если взять за основу х = (b1; b2;…; bm ;0;…;0) и представить это выражение псевдопланом, то, учитывая исходные данные, можно составить симплекс-таблицу. В ней часть элементов будет отрицательная. Так как дельта j должна быть больше либо равна нулю, то при отсутствии таких чисел в таблице уже будет записан оптимальный план. В обратном случае выбирается по модулю наибольшее из чисел с минусом.

Принцип решения задачи включает следующее:

• нахождение псевдоплана;
• проверка его на оптимальность;
• выбор разрешающей строки путём нахождения абсолютной величины отрицательного числа, отношения элементов (m+1) и соответствующей им строке;
• нахождение нового псевдоплана.

Если анализ оптимален, считается, что найдено верное решение. В другом случае устанавливается неразрешимость задачи либо составляется новый псевдоплан. Делается это в результате пересчёта табличных данных, например, методом Жордана-Гаусса.

Пример задачи

Использование метода линейного программирования распространено в решениях транспортных задач. Он помогает в целевых расчётах и нужен для минимизации затрат в условиях ограниченной грузоподъёмности и времени обслуживания заказчиков.

Задачи линейного программирования (ЗЛП) позволяют выбрать оптимальную загрузку при перемещении какого-либо товара из одних мест в другие. Во вводных данных указывается число пунктов отправления (м) и количество мест назначения (n). Первые обозначаются как А1, А2…Ам, а вторые – В1, В2…Вn. За аi принимается объём продукции на складе, а bi – потребность. Затраты на перевозку с i пункта в j обозначаются Сij.

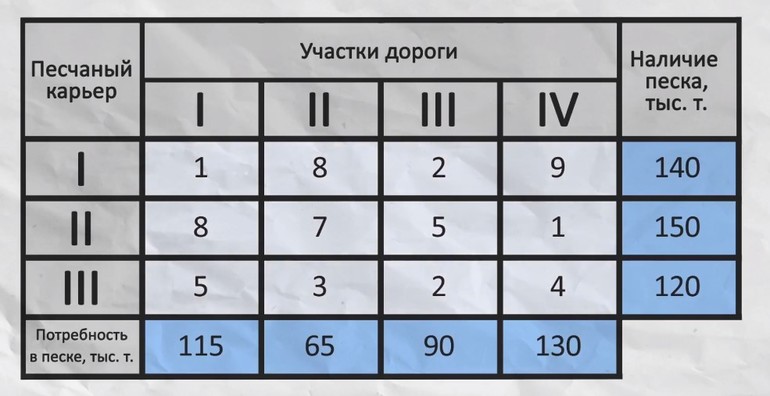
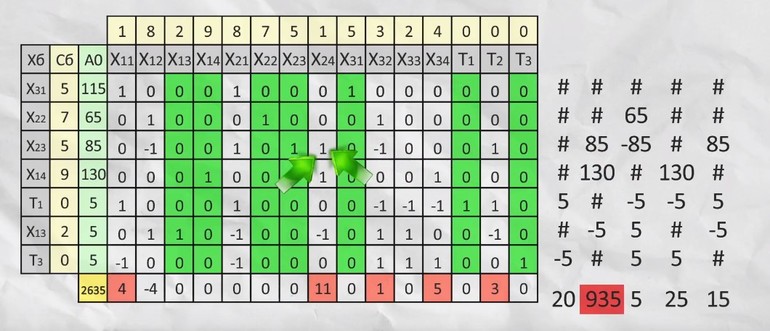
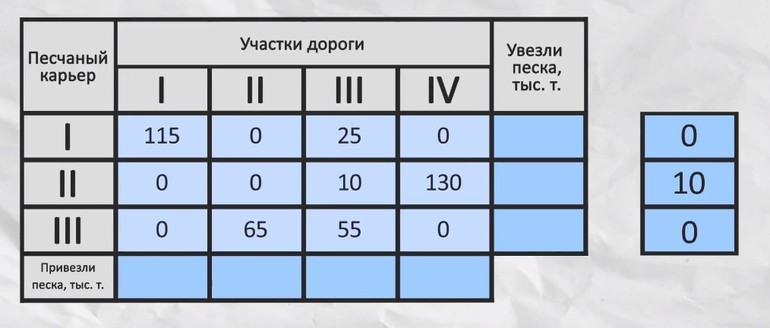
Главная задача — составить план таким образом, чтобы общая стоимость была минимальна. Пусть дано четыре песчаных карьера, с которых необходимо поставить песок на четыре склада. При этом осуществляться перевозки должны за определённую стоимость. Составляем таблицу.

Записываем уравнение ограничения. Сумма всего перевезённого песка с первого карьера должна быть меньше или равна 140. Поэтому можно записать: x11+x12+x12+x14+T1 = 140, где Т1 переменная для хранения остатка. Сумма ограничений будет записана как х11+х21+х31 =115. Аналогичные уравнения составляют и для оставшихся карьеров.

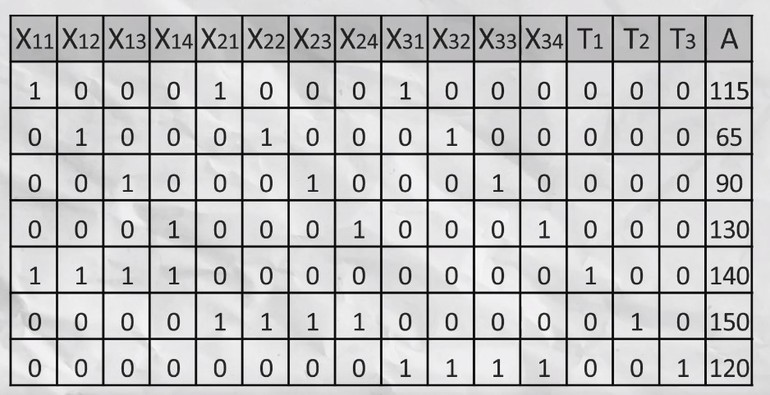
Теперь формируют матрицу, на основании которой с помощью свойства матриц ищется единичный базис. Например, вычесть из одной строки другую. Все отрицательные значения последнего столбца убирают. Для этого из каждой строки вычитают наименьшее значение, а последнее отрицательное число умножают на -1. Теперь составляют подробную симплекс-таблицу, где:

• A0 – последний столбец из матрицы;
• Сб – стоимость перевозок;
• Х11, Т3 – данные из полученной матрица.

В последней строчке прямоугольника проставляют сумму произведений Сб на этот столбец и вычитают значение суммы перемножения Сб с А0. Делают дополнительное вычисление. Для каждой строки А0 делят на выделенное число, ищут наименьший результат и умножают его на положительные числа из последней строки.

Наибольшее число определяется пересечением ранее выбранных значений, на базе которых создают новый базис. После в соответствии с единичными базисами меняют Сб и Хб. Операцию повторяют до тех пор, пока не исчезнут все положительные числа из последней строки. Заполняют новую таблицу.

Расчёт в Excel

Для включения пакета анализа в программе необходимо перейти в раздел «Параметры» и выбрать строчку «Перейти». В новом окне найти строчку «Пакет анализа», кликнуть по ней и нажать кнопку ОК.

Затем понадобится загрузить и открыть шаблон для проверки в Excel. Используя манипулятор типа «мышь» или клавиатуру, выбрать ячейку G4 и выполнить команду «Сервис/Поиск решения». Далее указать исходные данные, а после нажать кнопку «Выполнить».

Полученное решение можно представить в форме отчёта, содержащего:

1. Результаты – содержит информацию об исходных и конечных значениях целевой и влияющих ячеек, дополнительные сведения об ограничениях.
2. Устойчивость — отчёт, включающий данные о чувствительности решения к малым изменениям.
3. Пределы – включают исходные и конечные значения, а также верхние и нижние границы значений, которые принимают влияющие ячейки при введённых ограничениях.

Онлайн-сервис для чайников

Метод решения относится к высшей математике, поэтому в нём довольно трудно разобраться даже подготовленному человеку, не говоря уже о чайнике. Существует некоторое количество сайтов с подробным онлайн-решением методом симплекса. На таких сервисах предлагается ввести количество переменных и строк (ограничений). А далее просто заполнить симплекс-таблицу и нажать расчёт. Причём при необходимости вводимые данные можно править, тем самым видеть, как изменяется результат от изменения исходной информации.

Удобным является ещё и то, что обычно на сайтах предлагается создать шаблон решения в Excel или Maple. Решаться любая задача будет почти мгновенно. Подробно можно выполнить расчёт онлайн-калькулятор по методу симплекса на следующих сайтах:

1. «Семестр» (semestr.ru).
2. «Мир математики» (matworld.ru).
3. «Высшая математика» (math-pr.com).
4. «Матзона» (mathzone.ru).
5. «Контрольная работа» (kontrolnaya-rabota.ru).

Выполнить расчёт с помощью онлайн-сервисов сможет любой. При этом вероятность ошибки в ответе стремится к нулю. Тем более что для решения задачи даже необязательно знать принцип симплекс-метода.