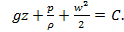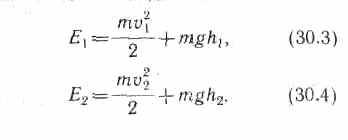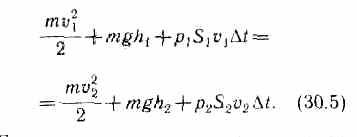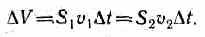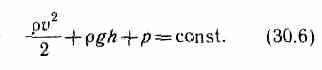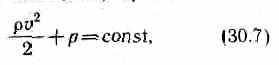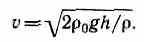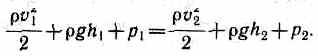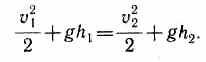Содержание
Неразрывным сплошным движением жидкости называется такое движение, когда внутри потока отсутствуют пустоты, нет разрыва струи.
Рассмотрим русло. В русле поток жидкости.
Выделим в русле элементарный прямоугольный параллелепипед с ребрами dx, dy и dz (параллелепипед неподвижен относительно стенок русла). Через стенки параллелепипеда течет сжимаемая жидкость ( 
.
 |
 |
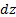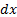L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEATyVrbcMA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESP0WrCQBRE34X+w3ILfdONQqOkrqKCpA+CJvYDLtnb JDR7N+xuY/r3XUHwcZiZM8x6O5pODOR8a1nBfJaAIK6sbrlW8HU9TlcgfEDW2FkmBX/kYbt5mawx 0/bGBQ1lqEWEsM9QQRNCn0npq4YM+pntiaP3bZ3BEKWrpXZ4i3DTyUWSpNJgy3GhwZ4ODVU/5a9R sB/laeicPy8Lf9lfq6Ps8/ys1NvruPsAEWgMz/Cj/akVpO9w/xJ/gNz8AwAA//8DAFBLAQItABQA BgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1s UEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxz UEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXht bC54bWxQSwECLQAUAAYACAAAACEATyVrbcMAAADbAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rv d25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIgDAAAAAA== " strokeweight="1.25pt"/>
 |
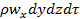| X |
| Y |
| Z |
 |
 |
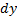Для составления ОБС определяем прежде всего субстанцию, для которой составляется ОБС; в качестве таковой служит масса жидкости.
Пространственным контуром является прямоугольный параллелепипед неподвижный относительно стенок русла.
Временной интервал – элементарный промежуток времени – 
.
В условиях неразрывности потока жидкости действуетзакон сохранения массы,поэтому из ОБС выпадают Источники и Стоки: +Пр – Ух = Нак
Составляем ОБС для параллелепипеда за время dt в направлении оси Х (потом Y и Z – по аналогии).
– приход жидкости, показывает массу жидкости которая вошла через левую грань параллелепипеда за время dt:
, где 
– плотность жидкости, которая может изменяться во времени и по координатам; 
– удельная массовая скорость жидкости.
– уход жидкости, показывает сколько жидкости вышло через правую грань за время dt:
.
.
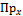
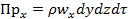
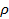
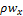
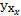
По аналогии записываем разности приходов и уходов для двух других направлений:
; 
;
Таким образом левая часть ОБС представляет собой выражение:
.
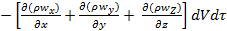
Остается выразить правую часть ОБС, а именно: Накопление массы жидкости в контуре за время dt. Количество массы в объеме параллелепипеда в момент времени 
равно 
. Полагая, что плотность жидкости является функцией только времени (в пределах выделенного объема), то Накопление массы жидкости в объеме параллелепипеда к моменту времени 
записывается в частных производных:
(т.к. выделенный объем неизменен).
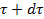
Собирая теперь найденные выше элементы ОБС, получаем после упрощения уравнение неразрывности в виде
Решение системы уравнений Навье-Стокса для частного случая: жидкость идеальна (m=0); несжимаемая (капельная ρ=const); среди внешних массовых сил действует только сила тяжести; движение жидкости стационарное и безвихревое. Диаграмма Бернулли для идеальной жидкости.
(безвихревое,– отсутствует вращательная составляющая жидкой частицы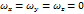 
)
Для указанных условий решение уравнений Навье – Стокса получают в виде интеграла Бернулли 
Каждый член уравнения имеет определенный физический смысл. (Размерность каждого члена этого уравнения 
. Умножим числитель и знаменатель на кг. Тогда получим размерность удельной энергии 
В этом случае первый член – удельная потенциальная энергия положения жидкости; второй – удельная потенциальная энергия давления жидкости; третий – удельная кинетическая энергия жидкости. Сумма этих удельных энергий представляет собой полную удельную энергию жидкости, которая одинакова в любом сечении потока.
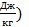
Поделив обе части уравнения Бернулли на g, получим
.
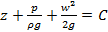
В практическом смысле уравнение Бернулли принято записывать для двух сечений потока
Размерность каждого члена уравнения – метр. Следовательно, существует и геометрический смысл каждого члена уравнения Бернулли: первый – нивелирная высота, второй – пьезометрическая высота, третий – скоростная высота. Сумма указанных высот потока идеальной жидкости при плоскости отсчета взятой произвольно, не зависит от выбранного сечения, т.е. остается величиной постоянной. Наряду с термином «высота» в гидравлике для этих слагаемых используют термин «напор». Сумму трех слагаемых называют полным напором.
На рисунке представлена графическая интерпретация уравнения Бернулли для безвихревого потока идеальной жидкости в форме так называемой диаграммы Бернулли.
 |
 |
 |
 |
| 1 |
| 1 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| С |
| С |
| В |
| В |
| А |
| А |
| Z1 |
| Z2 |
| Z3 |
 |
 |
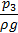| Диаграмма Бернулли для безвихревого потока идеальной жидкости в прямом трубопроводе постоянного поперечного сечения: О – О линия плоскости отсчета; А – А линия нивелирных высот; В – В линия пьезометрических высот; С – С линия полного напора. |
При решении задач это уравнение должно быть дополнено уравнением неразрывности в интегральной форме.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 – 
| 7302 – 
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Содержание
Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.
Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.
Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным. Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.
Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.
Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υср .
Таким образом уравнение расхода для потока будет
υср – средняя скорость потока
F – площадь сечения потока.
Уравнение неразрывности потока жидкости
Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.
Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный
а через сечение 2-2 из него же вытекает объем, равный
Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.
Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.
Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки
Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что
т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.
Уравнение неразрывности струи жидкости. Уравнение Бернулли.
Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.
При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.
Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.
Если всё это записать в виде формулы, то
где W – приращение кинетической энергии = m * υ 2 / 2
ΣA – сумма работ действующих сил = P *ΔS
В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.
Теперь рассмотрим обе части этого выражения по порядку.
Приращение кинетической энергии ΔW
В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.
Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.
Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен
масса в этом случае получается равной
Подставляя все это в выражение для кинетической энергии получаем цепочку
ΔW = m * υ 2 2 / 2 – m * υ 2 1 / 2 = ρ * q * ΔТ * υ 2 2 / 2 – ρ * q * ΔТ * υ 2 1 / 2
Работа сил действующих на систему ΣA
Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести AТ равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.
Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.
Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.
Силы давления АД , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.
Суммарно работа сил давления будет
Подставляя в начальное уравнение
Полученные выражения для ΔW и ΣA получаем
Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые
Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:
Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2
В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.
Видео по теме уравнение неразрывности
Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.
Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.
Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 45). Линии тока проводятся так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т. е. можно определить состояние движения жидкости. Линии тока в жидкости можно «проявить», например, подмешав в нее какие-либо заметные взвешенные частицы.
Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.
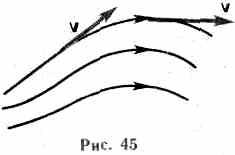
Рассмотрим какую-либо трубку тока. Выберем два ее сечения S1 и S2, перпендикулярные направлению скорости (рис. 46).
За время t через сечение S проходит объем жидкости Svt; следовательно, за 1 с через S1 пройдет объем жидкости S1v1, где v1 — скорость течения жидкости в месте сечения S1. Через сечение S2 за 1 с пройдет объем жидкости S2v2, где v2 — скорость течения жидкости в месте сечения S2. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (=const), то через сечение S2 пройдет такой же объем жидкости, как и через сечение S1, т. е.
Следовательно, произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение (29.1) называется уравнением неразрывности для несжимаемой жидкости.
§ 30. Уравнение Бернулли и следствия из него
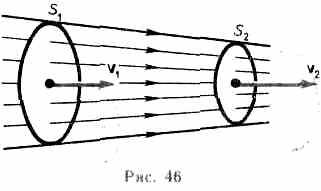
Выделим в стационарно текущей идеальной жидкости (физическая абстракция, т. е. воображаемая жидкость, в которой отсутствуют силы внутреннего трения) трубку тока, ограниченную сечениями S1 и S2, по которой слева направо течет жидкость (рис. 47). Пусть в месте сечения S1 скорость течения v1, давление р1 и высота, на которой это сечение расположено, h1. Аналогично, в месте сечения S2 скорость тече-
ния v2, давление р2 и высота сечения h2. За малый промежуток времени t жидкость перемещается от сечений S1 и S2 к сечениям S’1 и S‘2.
Согласно закону сохранения энергии, изменение полной энергии E2–Е1 идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы от жидкости:
где E1 и Е2 — полные энергии жидкости массой m в местах сечений S1 и S2 соответственно.
С другой стороны, А — это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S1 и S2, за рассматриваемый малый промежуток времени t. Для перенесения массы т от S1 до S’1 жидкость должна переместиться на расстояние l1= v1t и от S2 до S’2 — на расстояние l2= v2t. Отметим, что l1 и l2 настолько малы, что всем точкам объемов, закрашенных на рис. 47, приписывают постоянные значения скорости v, давления р и высоты h. Следовательно,
Полные энергии Е1 и e2 будут складываться из кинетической и потенциальной энергий массы m жидкости:
Подставляя (30.3) и (30.4) в (30.1) и приравнивая (30.1) и (30.2), получим
Согласно уравнению неразрывности для несжимаемой жидкости (29.1), объем, занимаемый жидкостью, остается постоянным, т. е.
Разделив выражение (30.5) на V, получим
где — плотность жидкости. Но так как сечения выбирались произвольно, то можем записать
Выражение (30.6) выведено швейцарским физиком Д. Бернулли (1700—1782; опубликовано в 1738 г.) и называется уравнением Бернулли. Как видно из его вывода, уравнение Бернулли — выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Оно хорошо выполняется и для реальных жидкостей, внутреннее трение которых не очень велико.
Величина р в формуле (30.6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина v 2 /2 — динамическим давлением. Как уже указывалось выше (см. § 28), величина gh представляет собой гидростатическое давление.
Для горизонтальной трубки тока (h1=h2) выражение (30.6) принимает вид
где р+v 2 /2 называется полным давлением.
Из уравнения Бернулли (30.7) для горизонтальной трубки тока и уравнения неразрывности (29.1) следует, что при те-
чении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно продемонстрировать, установив вдоль трубы ряд манометров (рис.48). В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.
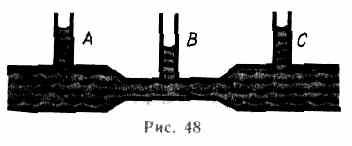
Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито — Прандтля (рис.49). Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоединены к манометру. С помощью одной из трубок измеряется полное давление (р), с помощью другой — статическое (р). Манометром измеряется разность давлений:
где — плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:
Из формул (30.8) и (30.9) получаем искомую скорость потока жидкости:
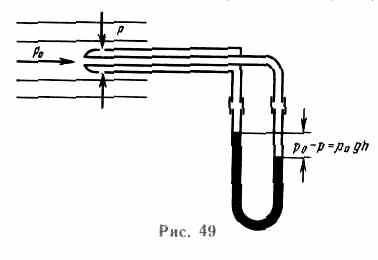
Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса (рис. 50). Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавливается и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст. = 133,32 Па).
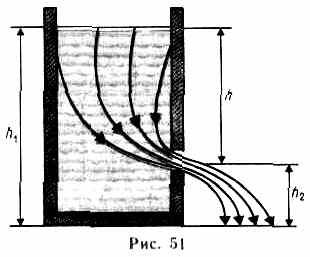
Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие (рис.51).
Рассмотрим два сечения (на уровне h1 свободной поверхности жидкости в сосуде и на уровне h2 выхода ее из отверстия). Напишем для них уравнение Бернулли:
Так как давления р1 и р2 в жидкости на уровнях первого и второго сечений равны
атмосферному, т. е. p1=p2, то уравнение будет иметь вид
Из уравнения неразрывности (29.1) следует, что v2/v1=S1/S2, где S1 и S2 — площади поперечных сечений сосуда и отверстия. Если S1>>S2, то членом v 2 1/2 можно пренебречь и
Это выражение получило название формулы Торричелли.
