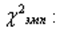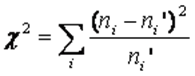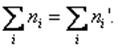Содержание
- 1 1. История разработки критерия корреляции
- 2 2. Для чего используется критерий корреляции Пирсона?
- 3 3. Условия и ограничения применения критерия хи-квадрат Пирсона
- 4 4. Как рассчитать коэффициента корреляции Пирсона?
- 5 5. Как интерпретировать значение коэффициента корреляции Пирсона?
- 6 6. Пример расчета коэффициента корреляции Пирсона
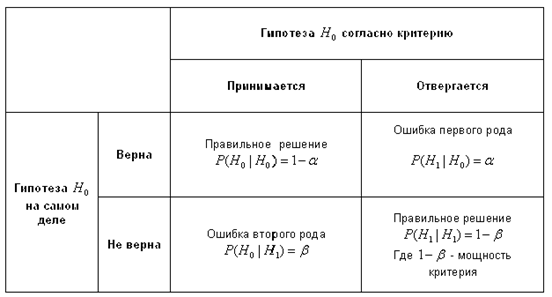
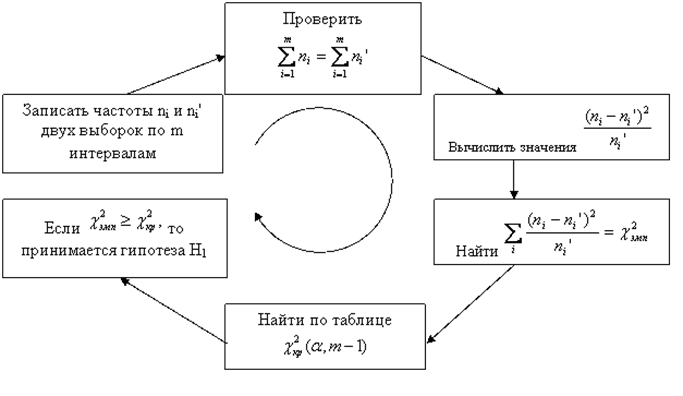
Критерий согласия для проверки гипотезы о законе распределения исследуемой случайной величины.Во многих практических задачах точный закон распределения неизвестен.Поэтому выдвигается гипотеза о соответствии имеющегося эмпирического закона, построенного по наблюдениям, некоторому теоретическому.Данная гипотеза требует статистической проверки, по результатам которой будет либо подтверждена, либо опровергнута.
Пусть X – исследуемая случайная величина. Требуется проверить гипотезу H о том, что данная случайная величина подчиняется закону распределения F(x). Для этого необходимо произвести выборку из n независимых наблюдений и по ней построить эмпирический закон распределения F'(x). Для сравнения эмпирического и гипотетического законов используется правило, называемое критерием согласия.Одним из популярных является критерий согласия хи-квадрат К. Пирсона.
В нем вычисляется статистика хи-квадрат:
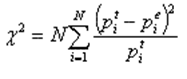
где N – число интервалов, по которому строился эмпирический закон распределения (число столбцов соответствующей гистограммы), i – номер интервала, p t i – вероятность попадания значения случайной величины в i-й интервал для теоретического закона распределения, p e i – вероятность попадания значения случайной величины в i-й интервал для эмпирического закона распределения. Она и должна подчиняться распределению хи-квадрат.
Если вычисленное значение статистики превосходит квантиль распределения хи-квадрат с k-p-1 степенями свободы для заданного уровня значимости, то гипотеза H отвергается.В противном случае она принимается на заданном уровне значимости.Здесь k – число наблюдений, p – число оцениваемых параметров закона распределения.
– Для сопоставления эмпирического распределения признака с теоретическим распределением (нормальным, показательным, равномерным либо каким-то иным законом);
– Для сопоставления двух эмпирических распределений одного и того же признака.
Идея метода – определение степени расхождения соответствующих частот ni и 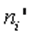
Объемы выборок должны быть не меньше 50 и необходимо равенство сумм частот
Приведем схему применения 
Критерий 
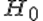
В зависимости от значения критерия 
§ 
§ 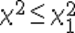
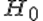
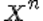
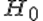
§ 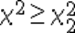
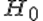
Определение: пусть дана случайная величина X .
Гипотеза 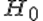
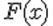
Для проверки гипотезы рассмотрим выборку, состоящую из n независимых наблюдений над с.в. X: 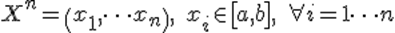
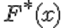
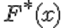
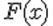

Гипотеза 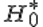
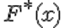
Разделим [a,b] на k непересекающихся интервалов 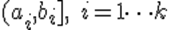
Пусть 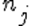
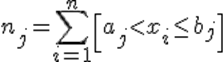
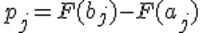
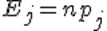
Статистика: 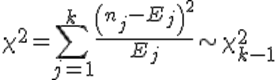
Критерий 
Критерий согласия Пирсона (χ 2 ) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.
Использование критерия χ 2 предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) nj для каждого из e интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины.
Число интервалов зависит от объема выборки. Обычно принимают: при n = 100 e = 10 ÷ 15, при n = 200 e = 15 ÷ 20, при n = 400 e = 25 ÷ 30, при n = 1000 e = 35 ÷ 40.
Интервалы, содержащие менее пяти наблюдений, объединяют с соседними. Однако, если число таких интервалов составляет менее 20 % от их общего количества, допускаются интервалы с частотой nj ≥ 2.
Статистикой критерия Пирсона служит величина
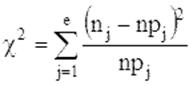
где pj – вероятность попадания изучаемой случайной величины в j-и интервал, вычисляемая в соответствии с гипотетическим законом распределением F(x). При вычислении вероятности pj нужно иметь в виду, что левая граница первого интервала и правая последнего должны совпадать с границами области возможных значений случайной величины.Например, при нормальном распределении первый интервал простирается до -∞, а последний – до +∞.
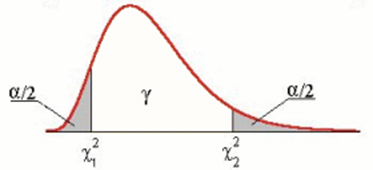
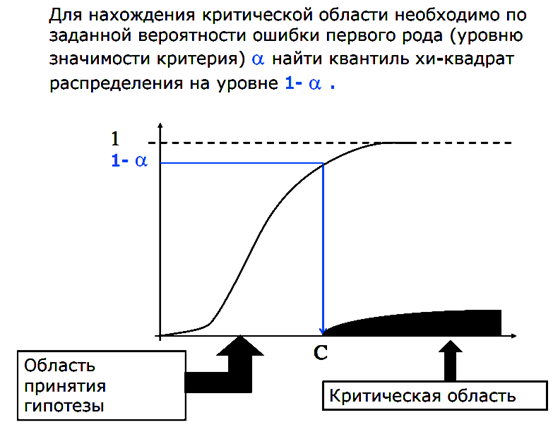
Нулевую гипотезу о соответствии выборочного распределения теоретическому закону F(x) проверяют путем сравнения вычисленной по формуле (3.91) величины с критическим значением χ 2 α, найденным по табл. VI приложения для уровня значимости α и числа степеней свободы k = e1 – m – 1. Здесь e1 – число интервалов после объединения; m – число параметров, оцениваемых по рассматриваемой выборке.Если выполняется неравенство
χ 2 ≤ χ 2 α (3.92)
то нулевую гипотезу не отвергают.При несоблюдении указанного неравенства принимают альтернативную гипотезу о принадлежности выборки неизвестному распределению.
Недостатком критерия согласия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы и объединения отдельных интервалов с малым числом наблюдений.В связи с этим рекомендуется дополнять проверку соответствия распределений по критерию χ 2 другими критериями.Особенно это необходимо при сравнительно малом объеме выборки (n ≈ 100).
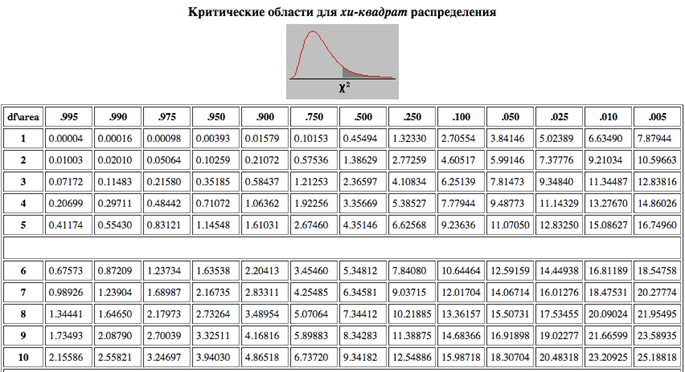
В таблице приведены критические значения хи-квадрат распределения с заданным числом степеней свободы.Искомое значение находится на пересечении столбца с соответствующим значением вероятности и строки с числом степеней свободы. Например, критическое значение хи-квадрат распределения с 4-мя степенями свободы для вероятности 0.25 составляет 5.38527. Это означает, что площадь под кривой плотности хи-квадрат распределения с 4-мя степенями свободы справа от значения 5.38527 равна 0.25.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8829 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Критерий согласия Пирсона (χ 2 ) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.
Использование критерия χ 2 предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) nj для каждого из e интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины.
Число интервалов зависит от объема выборки. Обычно принимают: при n = 100 e = 10 ÷ 15, при n = 200 e = 15 ÷ 20, при n = 400 e = 25 ÷ 30, при n = 1000 e = 35 ÷ 40.
Интервалы, содержащие менее пяти наблюдений, объединяют с соседними. Однако, если число таких интервалов составляет менее 20 % от их общего количества, допускаются интервалы с частотой nj ≥ 2.
Статистикой критерия Пирсона служит величина

где pj – вероятность попадания изучаемой случайной величины в j-и интервал, вычисляемая в соответствии с гипотетическим законом распределением F(x). При вычислении вероятности pj нужно иметь в виду, что левая граница первого интервала и правая последнего должны совпадать с границами области возможных значений случайной величины. Например, при нормальном распределении первый интервал простирается до -∞, а последний – до +∞.
Нулевую гипотезу о соответствии выборочного распределения теоретическому закону F(x) проверяют путем сравнения вычисленной по формуле (3.91) величины с критическим значением χ 2 α, найденным по табл. VI приложения для уровня значимости α и числа степеней свободы k = e1 – m – 1. Здесь e1 – число интервалов после объединения; m – число параметров, оцениваемых по рассматриваемой выборке. Если выполняется неравенство
χ 2 ≤ χ 2 α (3.92)
то нулевую гипотезу не отвергают. При несоблюдении указанного неравенства принимают альтернативную гипотезу о принадлежности выборки неизвестному распределению.
Недостатком критерия согласия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы и объединения отдельных интервалов с малым числом наблюдений. В связи с этим рекомендуется дополнять проверку соответствия распределений по критерию χ 2 другими критериями. Особенно это необходимо при сравнительно малом объеме выборки (n ≈ 100).
Пример 3.18. Проверить с помощью критерия согласия χ 2 гипотезу о нормальном распределении логарифма числа циклов до разрушения при усталостных испытаниях по данным табл. 2.3 и 2.4. Принять уровень значимости α = 0.05.
Все результаты вычислений приведены в табл. 3.18, данные первых трех граф которой заимствованы из табл. 2.4. В связи с малым числом наблюдений объединяем интервалы 1-й со 2-м и 9-й с 10-м и 11-м.
В 4-й графе приводим границы интервалов, выраженные через нормированную случайную величину 
где xср и s – соответственно выборочное среднее значение и среднее квадратическое отклонение логарифма числа циклов до разрушения образцов. Значения этих оценок были найдены в примере 2.2, xср = lg(N) = 6.515 и s = 0.315. С помощью табл. I приложения с учетом (1.29) находим значения функции Лапласа (1.27) для границ интервалов и заносим их в 5-ю графу. Оценка вероятности попадания значений механической характеристики в интервалы (6-я графа) представляет собой разность значений функции Лапласа на правой и левой границе интервала. Если интервалы объединяются, вычисляют разность значений функции на границах объединенного интервала. Сумма чисел pj, в графе 6 всегда будет равна единице. В 7-ю графу заносят оценки математических ожиданий числа наблюдений по интервалам, которые определяем умножением оценки вероятности pj на общее число образцов в выборке n =100. Итог 7-й графы должен равняться итогу 3-й графы.
Проверка гипотезы о нормальности распределения логарифма числа циклов до разрушения
Сумма 9-й графы дает значение статистики χ 2 . В данном случае χ 2 = 2.547.
По табл. VI приложения для α = 0.05 и k = 8 – 2 – 1 = 5 (8 – число интервалов после объединения, 2 – число параметров, оцениваемых по выборке, (xср, s) находим критическое значение критерия χ 2 0.05 = 11.1. Условие (3.92) выполняется, значит опытные данные не противоречат нормальному закону распределения, т. е. нулевую гипотезу не отбрасываем. К аналогичному выводу приходим и на основании графического метода (см. рис. 2.4).
Наблюденная в данном случае величина χ 2 = 2.547 соответствует фактическому уровню значимости α ≈ 0.75 (табл. VI приложения). Это означает, что если бы многократно повторить выборки по n = 100 из генеральной заведомо нормально распределенной совокупности, то значение χ 2 ≥ 2.547 встречалось бы примерно в 75 %.
Пример 3.19. Проверить с помощью критерия Пирсона нулевую гипотезу о распределении числа циклов до разрушения при усталостных испытаниях по закону Вейбулла – Гнеденко (1.46) для уровня значимости α = 0.06 по данным табл. 2.3 и 2.8.
Оценки параметров функции (1.46) были произведены в примере 2.4 (b = 0.721; xH = 0.736•10 6 циклов и c = 3.235•10 6 циклов).
Вычисление статистики χ 2 показано в табл. 3.19. В условиях рассматриваемого примера χ 2 = 35.091.
По табл. VI приложения для α = 0.05 и k = 11 – 3 – 1 =7 (11 – число интервалов после объединения, 3 – число оцениваемых по выборке параметров) находим критическое визчеине критерия Пирсона χ 2 0.05 = 14.1. Условие (3.92) не выполняется, значит опытные данные противоречат трехпараметрическому распределению Вейбулла – Гнеденко (1.46), т. е. нулевую гипотезу отвергаем. Нулевую гипотезу отбрасываем даже при уровне значимости α = 0.001, для которого критическое значение критерия χ 2 0.001 = 24.3.
К аналогичному выводу приходим и на основании графического анализа (см. рис. 2.5).
Проверка гипотезы о соответствии распределения числа циклов до разрушения трехпараметрическому распределению Вейбулла – Гнеденко
Подготовлено по публикации: Степнов М.Н. Статистические методы обработки результатов механических испытаний: Справочник. – М.: Машиностроение, 1985. – 232 с. Стр. 81 – 83.
Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката
Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"
– это метод параметрической статистики, позволяющий определить наличие или отсутствие линейной связи между двумя количественными показателями, а также оценить ее тесноту и статистическую значимость. Другими словами, критерий корреляции Пирсона позволяет определить, есть ли линейная связь между изменениями значений двух переменных. В статистических расчетах и выводах коэффициент корреляции обычно обозначается как rxy или Rxy.
1. История разработки критерия корреляции
Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.
2. Для чего используется критерий корреляции Пирсона?
Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.
Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.
3. Условия и ограничения применения критерия хи-квадрат Пирсона
- Сопоставляемые показатели должны быть измерены в количественной шкале (например, частота сердечных сокращений, температура тела, содержание лейкоцитов в 1 мл крови, систолическое артериальное давление).
- Посредством критерия корреляции Пирсона можно определить лишь наличие и силу линейной взаимосвязи между величинами. Прочие характеристики связи, в том числе направление (прямая или обратная), характер изменений (прямолинейный или криволинейный), а также наличие зависимости одной переменной от другой – определяются при помощи регрессионного анализа.
- Количество сопоставляемых величин должно быть равно двум. В случае анализ взаимосвязи трех и более параметров следует воспользоваться методом факторного анализа.
- Критерий корреляции Пирсона является параметрическим, в связи с чем условием его применения служит нормальное распределение сопоставляемых переменных. В случае необходимости корреляционного анализа показателей, распределение которых отличается от нормального, в том числе измеренных в порядковой шкале, следует использовать коэффициент ранговой корреляции Спирмена.
- Следует четко различать понятия зависимости и корреляции. Зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот.
Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.
В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.
Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов.
4. Как рассчитать коэффициента корреляции Пирсона?
Расчет коэффициента корреляции Пирсона производится по следующей формуле:
5. Как интерпретировать значение коэффициента корреляции Пирсона?
Значения коэффициента корреляции Пирсона интерпретируются исходя из его абсолютных значений. Возможные значения коэффициента корреляции варьируют от 0 до ±1. Чем больше абсолютное значение rxy – тем выше теснота связи между двумя величинами. rxy = 0 говорит о полном отсутствии связи. rxy = 1 – свидетельствует о наличии абсолютной (функциональной) связи. Если значение критерия корреляции Пирсона оказалось больше 1 или меньше -1 – в расчетах допущена ошибка.
Для оценки тесноты, или силы, корреляционной связи обычно используют общепринятые критерии, согласно которым абсолютные значения rxy 0.7 – о сильной связи.
Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:
| Абсолютное значение rxy | Теснота (сила) корреляционной связи |
| менее 0.3 | слабая |
| от 0.3 до 0.5 | умеренная |
| от 0.5 до 0.7 | заметная |
| от 0.7 до 0.9 | высокая |
| более 0.9 | весьма высокая |
Оценка статистической значимости коэффициента корреляции rxy осуществляется при помощи t-критерия, рассчитываемого по следующей формуле:
Полученное значение tr сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если tr превышает tкрит, то делается вывод о статистической значимости выявленной корреляционной связи.
6. Пример расчета коэффициента корреляции Пирсона
Целью исследования явилось выявление, определение тесноты и статистической значимости корреляционной связи между двумя количественными показателями: уровнем тестостерона в крови (X) и процентом мышечной массы в теле (Y). Исходные данные для выборки, состоящей из 5 исследуемых (n = 5), сведены в таблице:
| N | Содержание тестостерона в крови, нг/дл (X) | Процент мышечной массы, % (Y) |
| 1. | 951 | 83 |
| 2. | 874 | 76 |
| 3. | 957 | 84 |
| 4. | 1084 | 89 |
| 5. | 903 | 79 |
-
Вычислим суммы анализируемых значений X и Y:
Σ(X) = 951 + 874 + 957 + 1084 + 903 = 4769
Σ(Y) = 83 + 76 + 84 + 89 + 79 = 441
Найдем средние арифметические для X и Y:
| N | Содержание тестостерона в крови, нг/дл (X) | Процент мышечной массы, % (Y) | Отклонение содержания тестостерона от среднего значения (dx) | Отклонение % мышечной массы от среднего значения (dy) |
| 1. | 951 | 83 | -2.8 | 0.8 |
| 2. | 874 | 76 | -79.8 | -6.2 |
| 3. | 957 | 84 | 3.2 | 1.8 |
| 4. | 1084 | 89 | 130.2 | 6.8 |
| 5. | 903 | 79 | -50.8 | -3.2 |
| N | Содержание тестостерона в крови, нг/дл (X) | Процент мышечной массы, % (Y) | Отклонение содержания тестостерона от среднего значения (dx) | Отклонение % мышечной массы от среднего значения (dy) | dx 2 | dy 2 |
| 1. | 951 | 83 | -2.8 | 0.8 | 7.84 | 0.64 |
| 2. | 874 | 76 | -79.8 | -6.2 | 6368.04 | 38.44 |
| 3. | 957 | 84 | 3.2 | 1.8 | 10.24 | 3.24 |
| 4. | 1084 | 89 | 130.2 | 6.8 | 16952,04 | 46.24 |
| 5. | 903 | 79 | -50.8 | -3.2 | 2580,64 | 10.24 |
| N | Содержание тестостерона в крови, нг/дл (X) | Процент мышечной массы, % (Y) | Отклонение содержания тестостерона от среднего значения (dx) | Отклонение % мышечной массы от среднего значения (dy) | dx 2 | dy 2 | dx x dy |
| 1. | 951 | 83 | -2.8 | 0.8 | 7.84 | 0.64 | -2.24 |
| 2. | 874 | 76 | -79.8 | -6.2 | 6368.04 | 38.44 | 494.76 |
| 3. | 957 | 84 | 3.2 | 1.8 | 10.24 | 3.24 | 5.76 |
| 4. | 1084 | 89 | 130.2 | 6.8 | 16952,04 | 46.24 | 885.36 |
| 5. | 903 | 79 | -50.8 | -3.2 | 2580,64 | 10.24 | 162.56 |
Найдем значение суммы произведений отклонений Σ(dx x dy):
Рассчитаем значение коэффициента корреляции Пирсона rxy по приведенной выше формуле:
Найдем значение t-критерия для оценки статистической значимости корреляционной связи:
Критическое значение t-критерия найдем по таблице, где при числе степеней свободы f = n-2 = 3 и уровне значимости p = 0.01 значение tкрит = 5.84. Рассчитанное значение tr (7.0) больше tкрит (5.84), следовательно связь является статистически значимой.
Сделаем статистический вывод:
Значение коэффициента корреляции Пирсона составило 0.97, что соответствует весьма высокой тесноте связи между уровнем тестостерона в крови и процентом мышечной массы. Данная корреляционная связь является статистически значимой (p