Вращение линии вокруг оси

Одним из наиболее эффективных методов определения метрических характеристик плоских фигур является вращение вокруг оси, в качестве которой обычно используют линию уровня или проецирующую прямую.

Способ вращения вокруг проецирующей прямой

Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.

1. Траектория движения точки – дуга окружности с центром, расположенным на оси вращения. Радиус окружности равен расстоянию между точкой и осью вращения.
2. При вращении точки вокруг прямой, перпендикулярной фронтальной плоскости проекции, фронтальная проекция точки перемещается по дуге окружности, а горизонтальная – параллельно оси X.
3. При вращении точки вокруг прямой, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по дуге окружности, а фронтальная – параллельно оси X.

Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.

При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C’ переместим по дуге окружности радиусом C’D’ в положение C’₁ так, чтобы выполнялось условие C’₁D’₁ || X. Для нахождения точки C”₁ из C” проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C’₁.

На следующем рисунке показан способ перевода отрезка в горизонтально проецирующее положение. Построения выполнены в два этапа и описаны ниже.

Сначала вращением вокруг оси i₁ CD перемещают в положение C₁D₁, параллельное фронтальной плоскости проекции. После этого вращением вокруг оси i₂ отрезок переводится в искомое положение C₂D₂, где он перпендикулярен горизонтальной плоскости проекции.

Расположение осей вращения выбирают исходя из удобства дальнейших построений. В нашей задаче горизонтально проецирующая прямая i₁ проходит через точку D, а проекция i”₂ фронтально проецирующей прямой i₂ лежит на продолжении отрезка C”₁D”₁.

Способ вращения вокруг линии уровня

Действенным и наиболее рациональным приемом решения задач, в которых требуется определить натуральную величину угла, является способ вращения вокруг линии уровня.

Основные правила построения

1. Радиус вращения точки равен расстоянию между точкой и линией уровня, выполняющей роль оси. Натуральную величину радиуса определяют методом прямоугольного треугольника.
2. При вращении вокруг горизонтали h точка перемещается по окружности, которая проецируется на горизонтальную плоскость в отрезок прямой, перпендикулярный горизонтальной проекции горизонтали h’. На фронтальную плоскость окружность, по которой движется точка, проецируется в эллипс. Строить его нет необходимости.
3. При вращении вокруг фронтали f точка перемещается по окружности, которая проецируется на фронтальную плоскость в отрезок прямой, перпендикулярный фронтальной проекции фронтали f”. Вместе с тем горизонтальная проекция линии перемещения представляет собой эллипс, строить который не обязательно.

Рассмотрим, как определить действительную величину угла между прямыми a и b, пересекающимися в точке A. Построения представлены на рисунке и выполнены согласно алгоритму, который описан ниже.

1. Проводим фронтальную проекцию h” горизонтали h. Она пересекает прямые a” и b” в точках 1” и 2”. Определяем горизонтальные проекции 1′ и 2′ и через них проводим h’.
2. Находим центр вращения O. Его горизонтальная проекция O’ лежит на пересечении прямой h’ с перпендикуляром, проведенным из A’ к h’.
3. Определяем натуральную величину радиуса вращения R = O’A’. Для этого строим прямоугольный треугольник O’A’A’, катет которого A’A’ равен расстоянию от A” до h”.
4. Проводим дугу окружности радиусом R до пересечения её с прямой O’A’ в точке A’₁. Соединяем A’₁ с точками 1′ и 2′. Искомый угол ϕ построен.

Пиралова О. Ф., Ведякин Ф Ф.,

5.5. Способ вращения. Вращение вокруг проецирующей прямой

Сущность этого способа заключается в том, что система плоскостей проекций П2/П1 остается неподвижной, а положение геометрических элементов изменяется путем вращения вокруг одной или двух выбранных осей до нужного положения в данной системе. В качестве оси вращения в этом случае удобнее всего выбирать проецирующие прямые или прямые уровни, тогда точка будет вращаться в плоскостях, параллельных или перпендикулярных плоскостям проекций.

При вращении используются следующие элементы вращения:

– ось вращения – прямая, вокруг которой осуществляется вращение.

– плоскость вращения – плоскость, проходящая через вращаемую точку и перпендикулярная оси вращения (плоскость окружности, которую описывает точка при вращении).

– центр вращения – точка пересечения оси вращения и плоскости вращения.

– радиус вращения – кратчайшее расстояние от вращаемой точки до центра (оси) вращения. Радиус всегда перпендикулярен оси вращения.

– угол поворота – угол между начальным и конечным положением радиуса вращения.

При вращении системы точек вокруг одной оси все точки вращаются в плоскостях, параллельных между собой, поворачиваются на один и тот же угол в одном и том же направлении, поэтому вращение является частным случаем плоскопараллельного перемещения. Точки, находящиеся на оси вращения остаются неподвижными.

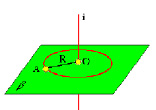
Способ вращения состоит в том, что данная геометрическая фигура вращается вокруг некоторой неподвижной оси до требуемого положения относительно неподвижных плоскостей проекций. При этом каждая точка фигуры, например точка А (рис. 5.13), описывает окружность, расположенную в плоскости β, перпендикулярной оси вращения i. Центр O этой окружности является точкой пересечения оси вращения с плоскостью β. Радиус окружности равен расстоянию точки А до оси i (|R| = |AO|).

При вращении точки вокруг оси, перпендикулярной горизонтальной плоскости проекций, ее фронтальная проекция перемещается перпендикулярно линиям связи, а горизонтальная – по окружности, центром которой является горизонтальная проекция оси вращения.

Рис. 5.13. Пример вращения точки вокруг оси,
перпендикулярной плоскости

При вращении точки вокруг оси, перпендикулярной фронтальной плоскости проекций, ее горизонтальная проекция перемещается перпендикулярно линиям связи, а фронтальная – по окружности, центром которой является фронтальная проекция оси вращения (рис. 5.14).

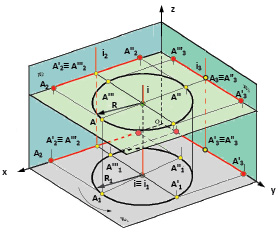
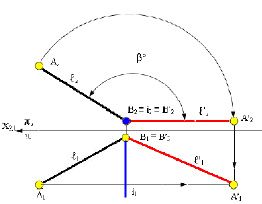
Рассмотрим вращение точки A(A1,A2,А3) вокруг горизонтально проецирующей прямой i (i1,i2,i3).

При вращении точка описывает окружность, плоскость которой β(β2) перпендикулярна оси i (i1,i2,i3). Поскольку i ⊥ П1, а β(β2) ⊥ i, β(β2) // П1 и угол поворота проецируется на П1 в натуральную величину.

Рассмотрим вращение точки A(A1,A2,А3) вокруг горизонтально проецирующей прямой i (i1,i2,i3).

При вращении точка описывает окружность, плоскость которой β(β2) перпендикулярна оси i (i1,i2,i3). Поскольку i ⊥ П1, а β(β2) ⊥ i, β(β2) // П1 и угол поворота проецируется на П1в натуральную величину.

Таким образом, при вращении вокруг горизонтально проецирующей прямой i(i1,i2) проекции точки A1, А’1, А"1, А"’1 перемещаются по окружности ℓ1 с центром в точке О1 и радиусом R = R1 = ОА = O1A1, фронтальные проекции A2, А’2, А"2, А"’2 перемещается по проекции фронтального следа плоскости β2 в пределах отрезка [А2,А"2].

Рассмотрим вращение точки A(A1,A2,А3) вокруг горизонтально проецирующей прямой i(i1,i2,i3).

Рис. 5.14. Пример вращения точки А вокруг
горизонтально проецирующей прямой i (i ⊥ П1)

При вращении точка описывает окружность, плоскость которой β(β2) перпендикулярна оси i(i1,i2,i3). Поскольку i ⊥ П, а β(β2) ⊥ i, β(β2) // П1 угол поворота проецируется на П1в натуральную величину.

Таким образом, при вращении вокруг горизонтально проецирующей прямой i(i1,i2) проекции точки A1, А’1, А"1, А"’1перемещаются по окружности ℓ1 с центром в точке О1 и радиусом R = R1= ОА = O1A1, фронтальные проекции A2, А’2, А"2, А"’2 перемещается по проекции фронтального следа плоскости β2 в пределах отрезка [А2, А"2].

Если точка А вращается вокруг оси i ⊥ П1, то плоскость β, в которой располагается окружность, описываемая точкой, становится горизонтальной плоскостью уровня (β || П1).

Следовательно, окружность, описываемая точкой А в пространстве, спроецируется на плоскость П1 без искажения, а на плоскость П2 – в отрезок прямой A2 А"2, совпадающей с фронтальным следом плоскости β2.

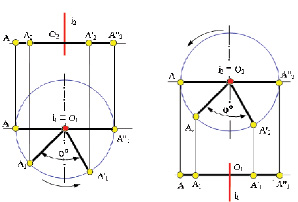
Таким образом, вращение точки A вокруг горизонтально проецирующей прямой i(i1,i2) на комплексном чертеже (рис. 5.15.а) изображено следующим образом:

1) горизонтальная проекция A1, точки А перемещается по окружности радиуса | R | = | АО | = | А1О1 |;

2) фронтальная проекция А2 точки А перемещается по прямой, перпендикулярной линиям связи (вырожденная фронтальная проекция β2 плоскости β ║П1);

3) угол поворота φ° горизонтальной проекции A1 точки А равен углу поворота точки в пространстве.

Рис. 5.15. Вращение точки А вокруг горизонтально проецирующей (а)
и фронтально проецирующей (б) прямых

Вращение точки A вокруг фронтально проецирующей прямой i(i1,i2) на комплексном чертеже (рис. 5.15.б) изображено следующим образом:

4) фронтальная A2, точки А перемещается по окружности радиуса R = | АО | = | А2О2 |;

5) горизонтальная проекция А1 точки А перемещается по прямой, перпендикулярной линиям связи (вырожденная горизонтальная проекция β1 плоскости β ║П2);

6) угол поворота φ° фронтальной проекции точки А равен углу поворота точки в пространстве.

Способом вращения тоже можно решать все основные на преобразование комплексного чертежа.

Задача 1. Преобразовать прямую общего положения в линию уровня.

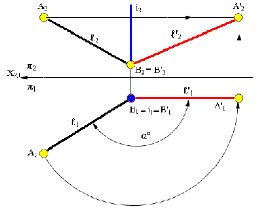
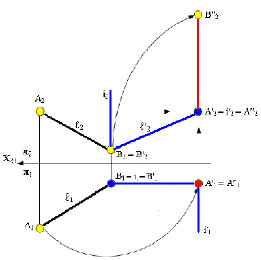
Для того чтобы прямую общего положения ℓ(ℓ1, ℓ2) преобразовать, например, во фронталь, ее необходимо вращать около оси i ⊥ П1 (рис. 5.16).

Рис. 5.16. Преобразование прямой линии общего положения
во фронтальную (фронталь) прямую

Для решения задачи необходимо:

1) выбрать две точки А(А1А2) и В(В1В2), принадлежащие прямой ℓ;

2) провести ось вращения i(i1,i2) перпендикулярно П1 через точку В(В1В2) прямой ℓ(ℓ1, ℓ2);

3) при вращении прямой ℓ вокруг оси i точка В прямой останется неподвижной, так как принадлежит оси, а точка А будет вращаться по правилам, рассмотренным выше;

4) угол поворота α° точки А и ее горизонтальной проекции А1 определяется между положением проекций А1В1 и А’1В’1.

Когда прямая ℓ займет положение параллельное П2, ее горизонтальная проекция ℓ’1 расположится перпендикулярно линиям связи.

Для определения положения проекции А’2 необходимо из А’1 провести вертикальную линию связи до пересечения с горизонтальной линией связи из фронтальной проекции А2. Пересечение этих двух линий связи определит новое положение проекции точки А’2.

Соединив между собой новые проекции точек, получим В’2А’2 натуральную величину прямой ℓ, что является решением первой задачи на преобразование комплексного чертежа.

Для преобразования прямой ℓ общего положения в горизонталь, ее необходимо вращать около оси i, перпендикулярной П2 и проходящей через какую-либо точку прямой (рис. 5.17).

Рис. 5.17. Преобразование прямой линии общего положения
в горизонтальную (горизонталь) прямую

Для преобразования, заданной прямой, необходимо:

1) выбрать две точки А(А1А2) и В(В1В2), принадлежащие прямой ℓ;

2) провести ось вращения i (i1,i2) перпендикулярно П2 через точку В(В1В2) прямой ℓ(ℓ1, ℓ2);

3) при вращении прямой ℓ вокруг оси i точка В прямой остаётся неподвижной, так как принадлежит оси, и новое её положение будет с ней совпадать В2 ≡ В’2, а точка А будет вращаться по правилам, рассмотренным выше;

4) угол поворота β° точки А и ее фронтальной проекции А2 определяется между положением проекций А2В2 и А’2В’2, когда прямая ℓ займет положение, параллельное П1, ее фронтальная проекция ℓ’2 расположится перпендикулярно линиям связи.

Для определения положения проекции А’1 необходимо из А’2 провести вертикальную линию связи до пересечения с горизонтальной линией связи из А1. Пересечение этих двух линий связи определит новое положение проекции точки А’1. Соединив между собой новые проекции точек, получим В’1А’1 натуральную величину прямой ℓ, что является решением первой задачи на преобразование комплексного чертежа.

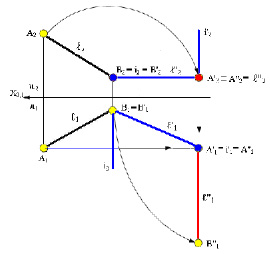
3адача 2. Преобразовать линию общего положения в проецирующую прямую (рис.5.18).

Рис. 5.18. Преобразование прямой линии общего положения
в горизонтально проецирующую

Вторую задачу на преобразование комплексного чертежа решать без решения первой задачи нельзя. Поэтому, если дана прямая общего положения, то для решения второй задачи необходимо выполнить два последовательных преобразования: вначале преобразовать ее в линию уровня (см. первую задачу), а затем линию уровня преобразовать в проецирующую (рис. 5.18, 5.19). Если линия уровня является фронталью, то ее можно преобразовать в горизонтально проецирующую прямую вращением около оси i’ перпендикулярной П2 (рис. 5.18). В рассматриваемом случае необходимо ось вращения провести через точку А’’. Во фронтальной плоскости проекций А’2 ≡ i’2 ≡ А’’2. Для определения нового положения точки В необходимо В’2 повернуть вокруг i’2 до положения В’’2. Соединив между собой новые проекции точек, получим В’’2А’’2, прямую перпендикулярную горизонтальной плоскости проекций (горизонтально проецирующую), что является решением второй задачи на преобразование комплексного чертежа.

Рис. 5.19. Преобразование прямой общего положения
во фронтально-проецирующую

Если линия уровня является горизонталью, то ее можно преобразовать во фронтально проецирующую прямую вращением около оси i’ перпендикулярной П1 (рис. 5.19). В рассматриваемом случае необходимо ось вращения провести через точку А’’.

В горизонтальной плоскости проекций А’1 ≡ i’1 ≡ А’’1. Для определения нового положения точки В необходимо В’1 повернуть вокруг i’1 до положения В’’1. Соединив между собой новые проекции точек, получим В’’1А’’1, прямую перпендикулярную фронтальной плоскости проекций (фронтально проецирующую), что является решением второй задачи на преобразование комплексного чертежа.

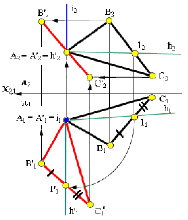
Задача 3. Преобразовать чертеж так, чтобы плоскость общего положения Σ(ΔАВС) после поворота стала проецирующей (рис. 5.20).

Рис. 5.20. Преобразование плоскости Σ(ΔАВС) во фронтально-проецирующую

При решении таких задач необходимо знать, что две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Таким образом, если какую-либо прямую, принадлежащую плоскости Г, преобразовать в проецирующую, то плоскость Г тоже станет проецирующей.

Для того чтобы плоскость преобразовать во фронтально проецирующую, ее необходимо вращать вокруг оси i ⊥ П1, а в качестве вспомогательной линии уровня взять горизонталь. Для решения этой задачи можно использовать плоскость треугольника ΔАВС. Если плоскость Г(ΔАВС) вращать вокруг оси i ⊥ П1, то горизонталь (h), принадлежащая плоскости, может быть повернута в положение, перпендикулярное плоскости П2, при этом плоскость Г станет фронтально проецирующей (рис. 5.20).

Построения новой горизонтальной проекции А’1В’1С’1 треугольника ΔАВС в плоскости нужно провести горизонталь (А111), которую одним поворотом сделать проецирующей прямой. За ось вращения i можно принять горизонтально проецирующую прямую, которую для удобства решения, провести через точку (А), принадлежащую плоскости. В горизонтальной плоскости проекций П1 проекции исходного и нового положения точки А и оси вращения совпадают А1 ≡ А’1 ≡ i1. При повороте точек В1 и С1 вокруг i1 величина их угла поворота равна величине угла поворота горизонтальной проекции горизонтали h1. В результате поворота треугольник ΔА’В’С’ оказывается перпендикулярным П2 и поэтому его фронтальная проекция В’2А2С’2 вырождается в прямую линию, построение которой необходимо выполнить по правилам, рассмотренным выше.

Фронтальные проекции начального и нового положений точки А совпадают А2 ≡ А’2. Положения точек В2 и С2 определяются в пересечении вертикальных и горизонтальных линий связи соответствующих точек. Для определения положения В’2 необходимо из В’1провести вертикальную, а из В2 горизонтальную линии связи. Для определения положения С’2 необходимо из С’1 провести вертикальную, а из С2 горизонтальную линии связи. Новые положения точек плоскости Г во фронтальной плоскости проекций П2 находятся на одной прямой, что подтверждает условие перпендикулярности Г ⊥ П2 и решение третьей задачи на преобразование комплексного чертежа.

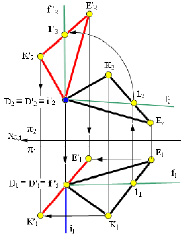
Для того чтобы плоскость Σ преобразовать в горизонтально проецирующую, её необходимо вращать вокруг оси i ⊥ П2, а в качестве вспомогательной линии уровня взять фронталь (рис. 5.21).

В качестве плоскости Σ можно использовать треугольник ΔDEK.

Если плоскость Σ (DEK) вращать вокруг оси i ⊥ П2, то фронталь (f), принадлежащая плоскости, может быть повернута в положение, перпендикулярное плоскости П1, при этом плоскость Σ станет горизонтально проецирующей (рис. 5.21).

Рис. 5.21. Преобразование плоскости Σ (ΔАВС) в горизонтально- проецирующую

Для построения новой горизонтальной проекции D’2E’2K’2 треугольника ΔDEK в плоскости нужно провести фронталь, которую одним поворотом сделать проецирующей прямой. За ось вращения i можно принять фронтально проецирующую прямую, которую для удобства решения, провести через точку (D), принадлежащую плоскости.

Во фронтальной плоскости проекций П2 проекции исходного и нового положения точки D и оси вращения совпадают D2 ≡ D’2 ≡ i2. При повороте точек E2 и K2 вокруг i2 величина их угла поворота равна величине угла поворота фронтальной проекции фронтали f2.

В результате поворота треугольник D’E’K’ оказывается перпендикулярным П1 и поэтому его горизонтальная проекция D’1 E11 K’2 вырождается в прямую линию, построение которой необходимо выполнить по правилам, рассмотренным выше.

Горизонтальные проекции начального и нового положений точки D совпадают D1 ≡ D’1. Положения точек E1 и K1 определяются в пересечении вертикальных и горизонтальных линий связи соответствующих точек. Для определения положения E’1 необходимо из E1 провести горизонтальную, а из E’2 вертикальную линии связи. Для определения положения К’1 необходимо из К1 провести горизонтальную, а из К’2 вертикальную линии связи. Новые положения точек плоскости Σ в горизонтальной плоскости проекций П1 расположены на одной прямой, что подтверждает условие перпендикулярности Σ ⊥ П1и решение третьей задачи на преобразование комплексного чертежа.

Рис. 10.9

Рассмотрим, как изменяется положение проекций точки при вращении ее вокруг оси, перпендикулярной к плоскости П₁ (рис. 10.10).

Рис. 10.10

При вращении точки М вокруг оси i^П₁ (центр вращения О, радиус вращения ОМ^i) на угол a , ее горизонтальная проекция М₁ перемещается по окружности (с центром в точке О₁ @ i₁) того же радиуса, в ту же сторону и на тот же угол a , что и сама точка М. Траектория движения точки М в пространстве на плоскость П₁ проецируется без искажения, т.к. она принадлежит плоскости Σ, параллельной П₁. Фронтальная проекция точки М(М₂) перемещается по прямой, параллельной оси ОХ.

Вращение геометрических фигур сводится к вращению конечного числа точек, определяющих данную фигуру. При этом полезно иметь в виду следующее:

а) точки, лежащие на оси вращения, не меняют своего положения, остальные точки вращаются в плоскостях, перпендикулярных оси вращения;

б) все вращающиеся точки поворачиваются в одну сторону на один и тот же угол;

в) если ось перпендикулярна некоторой плоскости проекций, то проекции на эту плоскость вращающейся фигуры в любом ее положении конгруэнтны. Последнее вытекает из рассмотренных свойств метода плоскопараллельного перемещения, т.к. вращение вокруг осей, перпендикулярных к плоскостям проекций представляет собой частный случай этого метода.

Рассмотрим, как осуществляется на эпюре перемещение отрезка общего положения в частное положение путем вращения вокруг оси перпендикулярной плоскостям проекций.

Пример 1. Отрезок АВ общего положения преобразовать в положение параллельное плоскости проекций П₂.

Чтобы осуществить такое преобразование, достаточно повернуть отрезок АВ вокруг оси i ^ П₁ на угол a. Для сокращения количества геометрических построений ось i ∋ В (рис. 10.11).

Величина угла a принимается такой, чтобы после поворота горизонтальная проекция отрезка заняла положение || ОХ. Так как точка В принадлежит оси вращения, то она не будет менять своего положения в процессе преобразования, следовательно, В₁ º В₁ // и В₂ º В₂ // . Для нахождения точки А₂ / необходимо из А₁ // провести вертикальную линию связи и отметить точку пересечения ее в горизонтальной прямой, проведенной через А₂.

Вращение вокруг линий уровня применяют в тех случаях, когда данную плоскую фигуру требуется совместить с какой-либо плоскостью, параллельной плоскости проекций. В таком положении плоская фигура проецируется на соответствующую плоскость проекций без искажения.

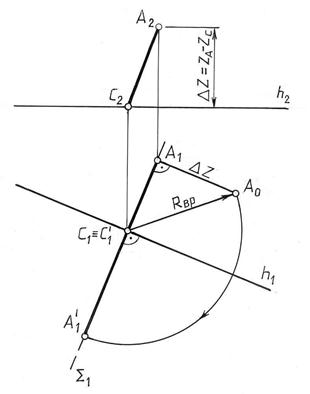
На рис. 10.12 показано вращение некоторой точки А вокруг горизонтальной оси h || П₁ . В этом случае плоскостью вращения точки А (плоскость, в которой расположена траектория движения точки А – окружность) будет являться плоскость Σ , перпендикулярная оси вращения (Σ^h) и, следовательно, горизонтальной плоскости проекций Σ^П₁ .

Точка А будет перемещаться по окружности с центром в точке С (точка пересечения оси вращения с плоскостью Σ). С=h∩Σ. Радиус этой окружности равен расстоянию от точки А до оси вращения h(R=АС).

Плоскость Σ – горизонтально проецирующая (Σ^П₁), поэтому траектория движения точки А в пространстве (окружность) спроецируется на плоскость П₁ в прямую, совпадающую с горизонтальным следом плоскости Σ (Σ_П1).

Когда точка А, вращаясь вокруг оси h, совместится с плоскостью, параллельной плоскости проекций П₁, радиус вращения этой точки R=CA займет горизонтальное положение и спроецируется на П₁ без искажения: C₁A₁=CA=R.

План решения задачи следующий:

1. Через горизонтальную проекцию А₁ точки А проведем горизонтальный след плоскости Σ (Σ₁^h₁) и отмечаем центр вращения С(С₁С₂).

2. Определяем натуральную величину радиуса вращения R_вр.=АС₁ (как гипотенузу прямоугольного треугольника, катетами которого являются горизонтальная проекция радиуса вращения А₁С₁ и разность координат Z точек А и С, ∆Z=Z_А–Z_C). Гипотенуза треугольника ∆С₁А₁А , С₁А=R_вр..

Новое, после поворота, положение точки А₁ / находится в месте пересечения дуги окружности, проведенной из горизонтальной проекции центра вращения С₁ радиусом, равным С₁А с горизонтальным следом Σ₁ плоскости Σ.

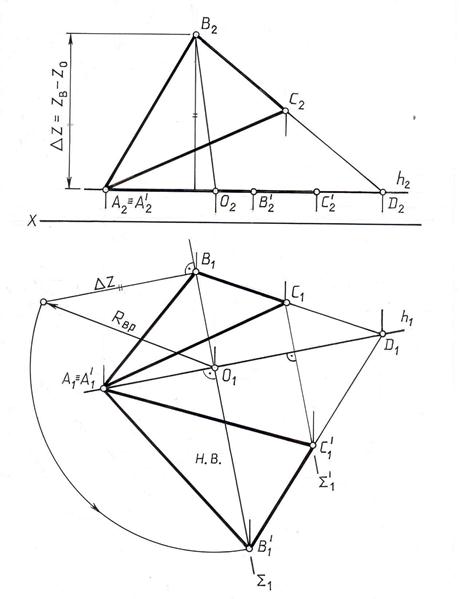
На рис. 10.13 показан пример вращения треугольника АВС вокруг его горизонтали АD(ADÌABC, AD||П₁). Точки D и А не меняют своего положения в процессе вращения треугольника (А₁ºА₁ / , D₁ºD₁ / ), т.к. они принадлежат оси вращения h(DÎh, АÎh), а горизонтальные проекции точек В и С перемещаются по прямым, перпендикулярным h₁ (B₁B₁ / ^h₁ и С₁С₁ / ^h₁). Положение точки В₁ / после поворота треугольника определено описанным выше способом (О₁В₁ / =О₁В=R_вр.). В результате вращения треугольник АВС занял положение А₁ / B₁ / C₁ / , параллельное плоскости П₁, и спроецировался на эту плоскость без искажений: çА₁ / В₁ / C₁ / ç= çABC ç. Фронтальная проекция треугольника после поворота А₂ / B₂ / C₂ / – прямая линия, параллельная оси координат.

Плоскости, касательные к поверхностям

Общие понятия. Способы построения касательных плоскостей.

Основные типы задач по построению касательных.

Плоскостью, касательной к криволинейной поверхности в обыкновенной точке А, называется плоскость, определяемая двумя пересекающимися прямыми, касательными к этой поверхности в точке А (рис. 11.1).

Обыкновенными точками поверхности являются точки, в которых можно построить только одну касательную плоскость к поверхности. Особыми точками поверхности считаются те, в которых нельзя построить только одну касательную плоскость. Примерами особых точек поверхности являются: вершина конуса, точка ребра возврата и т.д., касательная плоскость в которых может быть однозначно не определена, т.е. может быть проведено множество плоскостей.

Касательные плоскости применяются при построении линий пересечения поверхностей, при построении очерков поверхностей, при построении собственных теней поверхности, при построении нормали к поверхности и т.д.

Для того, чтобы провести прямую, касательную к поверхности в определенной ее точке, достаточно через эту точку провести на поверхности любую кривую и построить касательную прямую к ней. Поскольку через одну точку поверхности можно провести множество кривых линий, то в одной точке поверхности можно провести и множество касательных прямых.

Все эти касательные будут лежать в одной плоскости, являющейся касательной плоскостью к поверхности.

Таким образом, касательная плоскость к поверхности – это геометрическое место прямых, касающихся данной поверхности в обыкновенной точке.

Чтобы задать касательную плоскость, достаточно построить две касательные прямые к поверхности.

Касательной к поверхности называется прямая, являющаяся касательной к какой-либо линии, принадлежащей этой поверхности.

В качестве линий поверхности обычно используются линии ее определителя или линии, которые могут быть легко построены графически. Например, у поверхностей вращения это параллели и меридианы, у линейчатой поверхности – ее прямолинейные образующие.

Касательная плоскость может иметь с поверхностью только одну общую точку. В этом случае все линии поверхности, пересекающиеся в рассматриваемой точке, находятся по одну сторону от касательной плоскости. Такие точки поверхности называются эллиптическими. Поверхности, у которых все точки эллиптические, являются выпуклыми криволинейными поверхностями. К ним относятся сфера, эллипсоид вращения, параболоид вращения, закрытый тор и т. д.

Касательная плоскость может иметь с поверхностью общую линию (прямую или кривую). Например, касательная плоскость касается торсовых поверхностей вдоль их образующей – прямой линии. Она является касательной плоскостью для всех его точек, лежащих на этой прямой. Точки поверхности, удовлетворяющие этому условию, называются параболическими. К ним относятся точки развертываемых прямолинейных поверхностей – конических, цилиндрических и с ребром возврата.

Касательная плоскость к поверхности в данной точке может пересекать поверхность, к которой она проведена. В пересечении могут получаться пересекающиеся две прямые, две кривые, либо прямая и кривая линии.

Точки поверхности, касательная плоскость в которых пересекает поверхность, называются гиперболическими.Такие точки касания находятся на внутренней поверхности открытого тора.

Возможны следующие основные случаи построения касательных плоскостей к поверхностям:

1. через точку на самой поверхности

2. через точку, лежащую вне поверхности

3. параллельно заданной прямой

4. параллельно заданной плоскости

5. через прямую, лежащую вне поверхности

Построение касательной плоскости может выполняться несколькими способами:

1) построением двух касательных прямых к двум кривым линиям поверхности (обычно для эллиптических точек касания)

2) построением касательного следа плоскости к одноименному следу поверхности

3) построением вспомогательных сечений поверхности с последующим проведением к ним касательных прямых определенного направления

Последние два способа применяются обычно для гиперболических и параболических точек касания.

Рассмотрим примеры решения задач различных случаев.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8829 – | 7544 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно