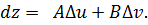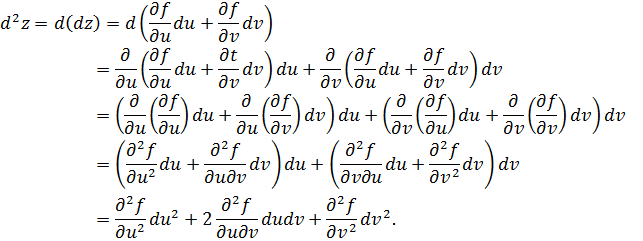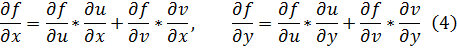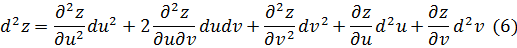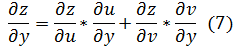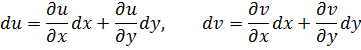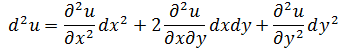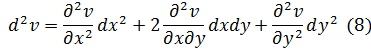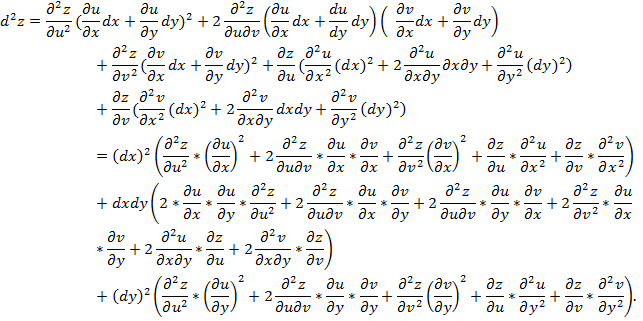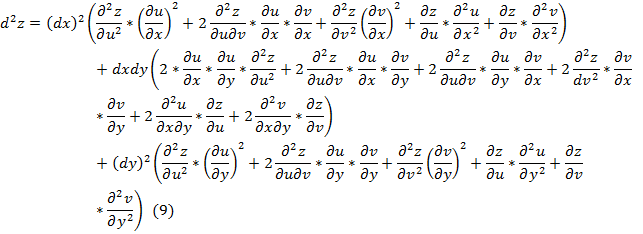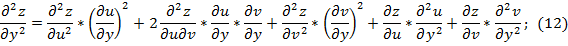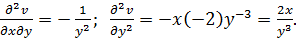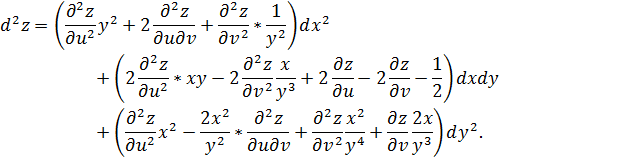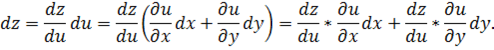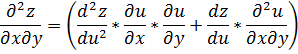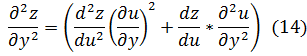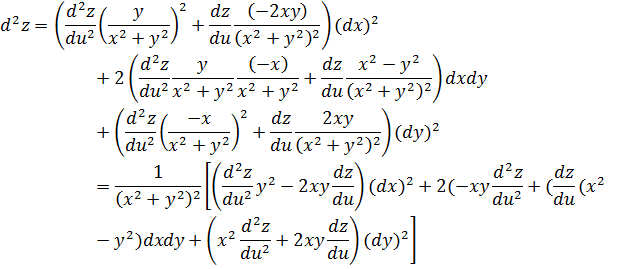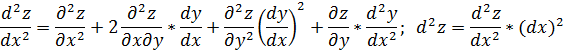Полный дифференциал для функции двух переменных:
- Примеры
≡ x^2/(x+2)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
Пусть f(x) дифференцируема в точке x и f ‘(x)≠0 , тогда ∆y=f’(x)∆x + α∆x, где α= α(∆x) →0 при ∆x→0. Величина ∆y и каждое слагаемое правой части являются бесконечно малыми величинами при ∆x→0. Сравним их: 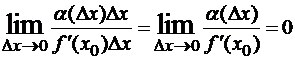
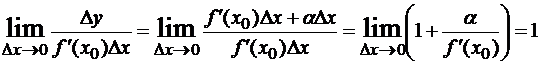
f’(x)∆x. Следовательно, f’(x)∆x представляет собой главную и вместе с тем линейную относительно ∆x часть приращения ∆y (линейная – значит содержащая ∆x в первой степени). Это слагаемое называют дифференциалом функции y=f(x) в точке x и обозначают dy(x) или df(x). Итак, для произвольных значений x
dy=f′(x)∆x. (1)
Полагают dx=∆x, тогда
dy=f′(x)dx. (2)
Пример . Найти производные и дифференциалы данных функций.
а) y=4 tg2 x
Решение:
дифференциал:
б)
Решение:
дифференциал:
в) y=arcsin 2 (lnx)
Решение:
дифференциал:
г)
Решение:

дифференциал:
Пример . Для функции y=x 3 найти выражение для ∆y и dy при некоторых значениях x и ∆x.
Решение. ∆y = (x+∆x) 3 – x 3 = x 3 + 3x 2 ∆x +3x∆x 2 + ∆x 3 – x 3 = 3x 2 ∆x+3x∆x 2 +∆x 3 ; dy=3x 2 ∆x (взяли главную линейную относительно ∆x часть ∆y). В данном случае α(∆x)∆x = 3x∆x 2 + ∆x 3 .
Найдем частные производные первого порядка:
Тогда дифференциал первого порядка равен:
Найдем частные производные второго порядка:
Тогда дифференциал второго порядка равен:
Ответ: 

Наука: Математика
- Условия публикаций
- Все статьи конференции
Статья опубликована в рамках:
Выходные данные сборника:
О ДИФФЕРЕНЦИАЛЕ ВТОРОГО ПОРЯДКА
Ловков Иван Юрьевич
студент Московского государственного университета информационных технологий, радиотехники и электроники, РФ, г. Серпухов
Таперечкина Вера Алексеевна
канд. физ.-мат. наук, доцент Московского государственного университета информационных технологий, радиотехники и электроники, РФ, г. Серпухов
ABOUT SECOND-ORDER DIFFERENTIAL
student of Moscow State University of Information Technologies, Radio Engineering and Electronics, Russia, Serpukhov
candidate of Physical and Mathematical Sciences, associate professor of Moscow State University of Information Technologies, Radio Engineering and Electronics, Russia, Serpukhov
В работе рассмотрены способы нахождения производных и дифференциалов первого и второго порядков для сложных функций двух переменных.
Calculation methods of derivative and first and second differentials for composite functions of two variables.
Ключевые слова: частные производные; дифференциал.
Keywords : partial derivatives; differential.
Сформулируем некоторые факты из теории функций многих переменных, которые понадобятся нам далее.
Определение: функция z=f(u, v) называется дифференцируемой в точке (u, v), если ее приращение Δz представимо в виде:
Линейная часть приращения называется полным дифференциалом и обозначается dz.
Теорема (достаточное условие дифференцируемости) см[1].
Если в некоторой окрестности т.(u, v) существуют непрерывные частные производные 


Определение: Вторым дифференциалом функции z=f(u, v) в данной точке (u, v) называется первый дифференциал от первого дифференциала функции f(u, v), т.е.
Из определения второго дифференциала z=f(u, v), где u и v – независимые переменные, следует
Таким образом, справедлива формула:

При выводе формулы использована теорема Шварца о равенстве смешанных производных 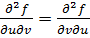
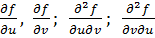
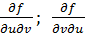
Формула для нахождения 2-го дифференциала может быть записана символически в следующем виде: 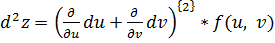
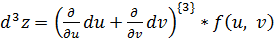


Отметим, что первый дифференциал функции двух переменных обладает свойством инвариантности формы. То есть, если u и v — независимые переменные, то для функции z=f(u, v), согласно (1)
Пусть теперь u=u(x y), v=v(x y), тогда z=f(u(x y), v(x y)), x и y — независимые переменные, тогда
Используя известные формулы для производной сложной функции:
Тогда из (3) и (4) получим:
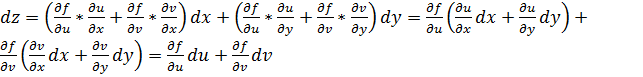
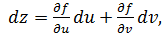
где 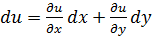

Сравнивая (1) и (5), видим, что формальная запись формулы для dz сохраняется, но если в (1) du=Δu, dv=Δv — приращения независимых переменных, то в (5) du и dv — дифференциалы функций u и v.
2. Второй дифференциал сложной функции двух переменных.
Прежде всего, покажем, что второй дифференциал не обладает свойством инвариантности формы.
Пусть z=z(u, v) в случае независимых переменных u и v второй дифференциал находим по формуле (2)
Пусть теперь u=u(x y), v=v(x y), z=z(u(x y), v(x y)), где независимые переменные x и y. Тогда
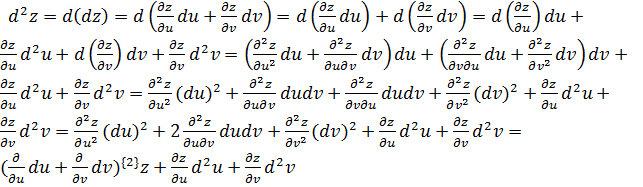
Итак, мы получили окончательно:
Формулы (2) и (6) не совпадают по форме, следовательно, второй дифференциал не обладает свойством инвариантности.
Ранее были выведены формулы частных производных 1-го порядка для сложной функции z=f(u, v), где u=u(x y), v=v(x y), где x и y — независимые переменные см [1].
Выведем формулы для вычисления частных производных и дифференциала второго порядка для функции z=f(u, v), u=u(x y), v=v(x y), где x и y — независимые переменные.
Для функций u(x y), v(x y) независимых переменных x, y имеем формулы:
Подставим формулы (8) в (6).
Таким образом, получили формулу для дифференциала второго порядка сложной функции двух переменных.
Сравнивая коэффициенты при 
Пусть z=f(u, v), u=xy, v=
Решение: вычисляем частные производные:

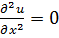


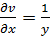
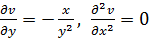
Подставив полученные результаты в (9), получаем ответ:
3. Важные частные случаи.
1. Рассмотрим случай, когда z=f(u, v), u=u(t), v=v(t).
Для первого дифференциала имеем:

Если в формуле (9) положить x≡t и учесть, что все производные по y отсутствуют, то получим:
Отметим, что в квадратных скобках формулы (13) стоит формула производной второго порядка для случая, если z=f(u, v), где u=u(t), v=v(t).
2. Рассмотрим случай, когда z=f(u), где u=u(x y).
Для первого дифференциала имеем:
Далее по формуле (6):
Сравнивая коэффициенты при 
Пусть 
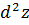
Решение: Обозначим u=
Находим второй дифференциал:
3. Рассмотрим случай, когда z=f(x y), y=y(x).
Для первого дифференциала имеем:
Далее из 1.получаем:
1.Архипов Г.И. Садовничий В.А. Чубариков В.Н. Лекции по математическому анализу. М.: Дрофа, 2004
2.Виноградова И.Л. Олехник С.Н. Садовничий В.А. Задачи и упражнения по математическому анализу М.В.Ш., 2002
3.Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука,1990.
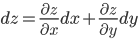
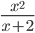 ≡ x^2/(x+2)
≡ x^2/(x+2) 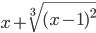 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)