
] в лорановском разложении этой функции в точке z0. Отсюда, в частности, вытекает, что вычет в устранимой особой точке равен нулю. Укажем некоторые формулы для вычисления вычета в полюсе функции /(г). 1. zq — полюс первого порядка: 00 Умножим обе части этого равенства на z – zo и, переходя к пределу при z zo, получим, что Если функцию f(z) можно представить в виде дроби где и ф(г) — аналитические функции, причем простой полюс, то из формулы (3) вытекает, что Пример 1. Пусть Особые точки » функции , ЯВЛЯЮТСЯ простыми гюлюсами. Поэтому 2. zo — полюс порядка т: Для устранения отрицательных степеней z – z0 умножим обе части этого равенства на (z-Zo)m, Вычеты Основная теорема о вычетах Применение вычетов к вычислению интегралов Вычет функции относительно бесконечно удаленной точки Приложение вычетов к вычислению определенных интегралов Интегралы от рациональных функций Лемма Жордана Вычисление интегралов Френеля Продифференцируем полученное соотношение m – 1 раз и, переходя к пределу при получим, что Пример 2. Пусть 4 Особыми точками этой функции являются точки г = ±i. Это — полюсы второго порядка. Вычислим, например, res/(i). Имеем Теорема 21i Пусть функция f(z) аналитична всюду в области D за исключением конечного числа изолированных особых точек 7огда для любой замкнутой области G, лежащей в D и содержащей точки zn внутри, справедливо равенство Теорема вытекает из теоремы Коши для многосвязной области. Построим окруж ности столь малого радиуса г, что ограниченные ими круги — содержатся в области G и не пересекаются друг с другом (рис. 29). Обозначим через G* область, которая получается из области G путем удаления кругов Uи . U„. Функция f(z) анали-тична в области G* и непрерывна в ее замыкании G7. Поэтому по теореме Коши для многосвязной области имеем Из этой формулы, пользуясь определением вычета получаем требуемое равенство (5). 6.1. Вычет функции относительно бесконечно удаленной точки Говорят, чтофункция f(z) является аналитической в бесконечно удаленной точке z = оо, если функция аналитична вточке С =0. Это следует понимать так: функцию g(0= f (f) можно доопределить до аналитической, положив Например, функция аналитична в точке z = оо, поскольку функция аналитична в точке С = 0. Пусть функция /(г) аналитична в некоторой окрестности бесконечно удаленной точки (кроме самой точки z = оо). Точка z = оо называется изолированной особой точкой функции /(г), если в некоторой окрестности этой точки нет других особых точек функции f(z). Функция имеет в бесконечности неизолированную особенность: полюсы zk = к-к этой функции накапливаются в бесконечности, если к оо. Говорят, что z — оо является устранимой особой тонкой, полюсом или существенно особой точкой функции f(z) в зависимости от того, конечен, бесконечен или вовсе не существует lim f(z). Критерии типа бесконечно удаленной точки, связанные с разложением Лорана, изменяюгся по сравнению с критериями для конечных особых точек. Теорема 22. Если z — оо является устранимой особой точкой функции /(z), то лоранов-ское разложение f(z) в окрестности этой точки не содержит полож и тельных степеней z;eaiu z — оо — полюс, то это разложение содержит конечное число положительных степеней z, в случае существенной особенности — бесконечное число положительных степеней z. При этом лорановским разложением функции /(z) в окрестности бесконечно удаленной точки будем называть разложение в ряд Лорана, сходящийся всюду вне круга достаточно большого радиуса R с центром в точке z — 0 (кроме, быть может, самой точки z — оо). Пусть функция f(z) — аналитична в некоторой окрестности точки z = оо (кроме, быть может, самой этой точки). Вычетом функции /(z) в бесконечности называют величину пае 7 — достаточно большая окружность z = р, проходимая по часовой стрелке (так, что окрестность точки z — оо остается слева, как и в случае конечной точки г = го). И з этого определения следует, что вычет функции в бесконечности равен коэффициенту при z
! в лорановском разложении /(z) в окрестности точки z — оо, взятому с противоположным знаком: Пример 3. Для функции f(z) = имеем f(z) = 1 + j. Это выражение можно рассматривать как ее лорановское разложение в окрестности +очки z = оо. Легко видеть, что так что точка z = оо является устранимой особой точкой, и мы полагаем, как обычно, /(оо) = 1. Здесь , следовательно, Из этого примера следует, что вычет аналитической функции относительно бесконечно удаленной устранимой особой точки (в отличие от конечной устранимой особой точки) может оказаться отличным от нуля. Известные тейлоровские разложения функций е1, cosz, sinz, chz, shz можно рассматривать также и как лорановские разложения в окрестности точки z — оо. Так как все эти разложения содержат бесконечное множество положительных степеней z, то перечисленные функции имеюгвточке z = оо существенную особенность. Теорема 23. Если функция f(z) имеет в расширенной комплексной плоскости конечное число особых точек, то сумма всех ее вычетов, включая и вычет в бесконечности, равна нулю. Так что, если — конечные особые точки функции f 0 — вещественное число. При вычислении таких интегралов часто бывает полезной следующая лемма. Лемма Жордана. Пусть функция f(z) аналитична в верхней полуплоскости исключением конечного числа изолированных особых точек, и при стремится к нулю равномерно относительно arg z. Тогда для любого положитыьного а где 7л — верхняя полуокружность Условие равномерного стремления /(г) к нулю означает, что на полуокружности 7R Оценим исследуемый интефал. Замечая, что на 7Л В силу известного неравенства (см. рис. 31) справедливого при (для доказательства достаточно заметить, что и, значит, функция ^ убывает на полуинтервале Сопоставляя формулы (13) и (14), заключаем, что 4 Введем вспомогательную функцию Пример 7. Вычислить интеграл Нетрудно видеть, что если г = х, то Jmh(z) совпадает с подынтегральной функцией Рассмотрим контур, указанный на рис.32. При достаточно большом R на дуге 7л Функция вследствие соотношения , удовлетворяет условию при Значит, по лемме Жордана По основной теореме о вычетах для любого имеем Переходя к пределу в равенстве (16) и учитывая соотношение (15). получим, что Разделяя слева и справа вещественные и мнимые части, будем иметь В силу того что подынтегральная функция f(x) — четная, окончательно получим В рассматриваемом примере функция f(z) не имеет особых точек на действительной оси. Однако небольшое изменение описанного метода позволяет применять его и в том случае, когда функция f(z) имеет на действительной оси особые точки (простые полюсы). Покажем, как это делается. Пример 8. Вычислить интеграл 4 функция обладает следующими свойствами: при совпадает с подынтегральной функцией; 2) имеет особенность на действительной оси — простой полюс в точке г = 0. Рассмотрим в верхней полуплоскости Im z ^ 0 замкнутый контур Г, состоящий из отрезков действительной оси [-Я, -г), (г,R) и дуг полуокружностей (рис. 33). Внутри этого контура находится лишь один полюс функции h(z) — точка z = Ы. Согласно основной теореме о вычетах, Преобразуем сначала сумму интегралов по отрезкам (-Я, -г| и |г, Я) действительной оси. Заменяя х на
х в первом слагаемом правой части равенства (18) и объединяя его с третьим слагаемым, получим Обратимся ко второму слагаемому в формуле (18). Так как где lim g(z) = 0. то подынтегральная функция h(z) представима в следующем виде: Тогда Полагая . получим, что Четвертое слагаемое в равенстве (18) при Я —» оо стремится к нулю согласно лемме Жордана, ибо функция ^ стремится к нулю при |г| оо. Таким образом, при равенство (18) принимает вид 6.3. Вычисление интегралов Френеля Интегралы Френеля: Рассмотрим вспомогательную функцию /(г) = с" и контур Г, указанный на рис. . Внутри контура Г функция f(z) — аналитическая, и по теореме Коши Покажем, что где Гг2 — полуокружность радиуса г2. Функция 0(0 = удовлетворяет условиям леммы Жордана, и, значит, Переходя в формуле (20) к пределу при г -* оо, получим, что На отрезке ВО: Отсюда откуда Упражнения Найдите действительную и мнимую части функдаи: Найдите образы действительной и мнимой осей при отображении: Докажи те, что функция непрерывна на всей комплексной плоскости: Пользуясь условиями Коши—Римана, выясните, является ли функция аналитической хотя бы в одной точке или нет: Восстановите аналитическую в окрестности точки 20 функцию /(г) по известной действительной части и (или по известной мнимой части v(x, у)) и значению f(z0): Покажите, что следующие функци и являются гармоническими: Может ли данная функция быть действительной или мнимой частью аналитической функции Найдите действительную и мнимую части функции: Найдите модуль и главное значение аргумента функции в указанной точке zq: Найдите логарифмы следующих чисел: Решите уравнение: 38. Вычислите интеграл /— линия, соединяющая точки z = 0 отрето к прямой, б) дуга параболы ломаная 39. Вычислите интеграл — полуокружность Вычислите интегралы: 43. Вычислите интеграл / где 7 — верхняя половина окру*« ости |z| = 1 (выбирается Вычеты Основная теорема о вычетах Применение вычетов к вычислению интегралов Вычет функции относительно бесконечно удаленной точки Приложение вычетов к вычислению определенных интегралов Интегралы от рациональных функций Лемма Жордана Вычисление интегралов Френеля ветвь функци и л/z, для которой 44. Вычислите интеграл / ^ dz, где 7 — отрезок прямой, идущий из точки zj = 1 в точку Вычислите интегралы: Найдите радиус сходимости ряда: Рашожите функцию в ряд Тейлора и найдите радиус сходимости полученного ряда: постепеням z + I. 55. cosz постепеням 56.—-— постепеням z + 2. 57.—^— постепеням z. 58. sh2 z постепеням z. Найдите нули функции и определите их порядки: z Определите область сходимости ряда: Разложите в ряд Лорана в окрестности точки г = 0: Разяожитс в ряд Лорана в уюзан ном кольце: Найдите особые точки и определит е их характер: Найдите вычеты функции в особых точках : Вычислите интегралы: Определите характер бесконечно удаленной точки: Вычислите интегралы: Ответы z переходите ось ы, при изменении z от -оо до +оо и изменяется от до -оо и от +оо до +1 (точка +1 исключается), ось у переходит в окружность Ось х переходит в ось и так же, как и в упр-и 5, ось у переходит в прямую u
1, пробегаемую от точми 1 до 1 + too и от 1 – »оо до точки 1 (сама точка 1 исключается
Определение. Точки комплексной плоскости, в которых однозначная функция f(z) является аналитической, называют правильными точками этой функции, а точки, в которых f(z) не является аналитической, называют особыми точками (в частности, точки, в которых f(z) не определена).
Определение. Точка z называется нулем (корнем) порядка (кратности) аналитической функции f(z),если:
б) существует, конечен и не равен нулю.
Если целые положительные числа), тогда – нули (корни) этого многочлена, которые имеют соответственно порядки (кратности) .
Определение. Пусть f(z) аналитическая функция в окрестности точки z, за исключением самой точки z. В этом случае точка z называется изолированной особой точкой функции f(z).
Различают изолированные особые точки однозначной функции трёх типов:
1) устранимую особую точку – изолированную особую точку z , в которой существует конечный предел:
2) полюс k-го порядка – изолированную особую точку z, в которой существует конечный предел, не равный нулю:
если , то z – полюс первого порядка (простой полюс);
3) существенно особую точку – изолированную особую точку z, которая не является ни устранимой, ни полюсом. То есть не существует, ни конечный, ни бесконечный.
Теорема (о связи между нулем и полюсом). Если точка z – нуль порядка к функции f(z), то для функции 1/f(z) эта точка является полюсом порядка к.
Пусть f(z) – функция, аналитическая в каждой точке области D, за исключением конечного числа изолированных особых точек, и L — кусочно-гладкий замкнутый контур, целиком лежащий в области D и не проходящий через особые точки функции f(z).
Если в области, ограниченной контуром L, не содержится особых точек функции f(z), то по основной теореме Коши
Если же в области, ограниченной контуром L, имеются особые точки функции f(z), то значение этого интеграла, вообще говоря, отлично от нуля.
Определение. Вычетом аналитической функции f(z) относительно изолированной особой точки z (или в точке z) называется комплексное число, равное значению интеграла , где L – любой кусочно-гладкий замкнутый контур, лежащий в области аналитичности функции f(z) и содержащий внутри себя единственную особую точку z функции f(z).
Вычет f(z) относительно точки z обозначается символом resf(z)(Resf(z)) или так, что имеем:
Вычет функции относительно устранимой особой точки равен нулю:
Вычет f(z) относительно простого полюса можно найти по формуле:
Вычет f(z) относительно полюса порядка к находят по формуле:
Если причем точка является простым нулем и не является нулем для , то:
Основная теорема Коши о вычетах. Если функция f(z) аналитическая в замкнутой области , ограниченной контуром L, за исключением конечного числа особых точек , лежащих внутри ,то:
Эта теорема имеет большое значение для приложений.
Замечание. В предыдущих рассуждениях о вычетах неявно предполагалось, что рассматриваются конечные изолированные особые точки (это ясно из того, что интеграл по замкнутому контуру по умолчанию брался в положительном направлении, т.е. против часовой стрелки, а особая точка при этом попадает внутрь контура только в случае, когда она конечна). В случае же, когда рассматривается бесконечно удаленная точка, ситуация несколько иная. Точнее, сформулируем это так.
Определение. Вычетом функции f(z) относительно бесконечно удаленной точки называют интеграл:
где L – замкнутый кусочно-гладкий контур, целиком лежащий в той окрестности точки , в которой функция f(z) является аналитической. Интегрирование по Lсовершается в отрицательном направлении этого контура, т.е. так, чтобы при обходе контура бесконечно удаленная точка оставалась слева. Таким образом:
Найти интеграл от функции комплексного переменного, используя основную теорему Коши о вычетах:
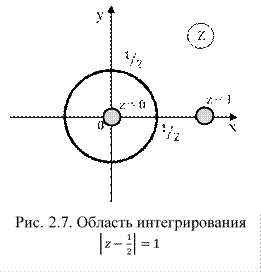
1) Определим изолированные особые точки подинтегральной функции, согласно теореме (2.47):
2) Определим точки, лежащие внутри области интегрирования, изобразим область графически (рис. 2.7).
Точку z = 1 не рассматриваем, так как она не лежит внутри области .
3) Определим тип рассматриваемой изолированной особой точки z = 0. Найдем предел по формуле (2.41):
Так как предел существует, то z = 0 – полюс первого порядка (простой полюс).
4) Найдем вычет функции относительно простого полюса z = 0, используя формулу (2.44):
5) Определим значение интеграла по основной теореме Коши о вычетах (2.47):
Найти интеграл от функции комплексного переменного, используя основную теорему Коши о вычетах:

1) Определим изолированные особые точки подинтегральной функции, согласно теореме (2.47):
2) Определим точки, лежащие внутри области интегрирования, изобразим область (рис. 2.8).
Обе особые точки лежат внутри области интегрирования.
3) Определим тип рассматриваемых изолированных особых точек . Найдем предел по формуле (2.41):
так как предел существует, то z = -1 – полюс первого порядка (простой полюс).
так как предел существует, то z = -2 – полюс первого порядка (простой полюс).
4) Найдем вычеты функции относительно простых полюсов и используя формулу (2.44):
5) Определим значение интеграла по основной теореме Коши о вычетах (2.47)
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
1. Вычисление интегралов по замкнутому контуру. Пусть функция f(z) имеет внутри замкнутого контура Г только изолированные особые точки. Тогда интеграл от f(z) по контуру Г можно найти, применяя теорему 27.1 о вычетах: вычисляя вычеты в особых точках, находящихся внутри контура Г, складывая эти вычеты и умножая сумму на 2тгг, мы и получим искомый интеграл.
Г1 р и м е р 28.1. Вычислить интеграл
Р е ш е н и е. Внутри окружности z = 2 находятся две особые точки функции f(z) = ( 22 +i)(^+ 3) 2 ’ а именно z i = U z 2 = —Ц третья особая точка z% = — 3 лежит вне этой окружности. Вычеты в точках ±г были найдены в примере 27.5: res*/ = 0,01(7-N), res_*/ = 0,01(7— г). Применяя формулу (27.2), имеем:

Если функция f(z) имеет в расширенной комплексной плоскости С только изолированные особые точки, то вместо вычисления суммы вычетов в конечных особых точках бывает проще найти вычет в бесконечно удаленной точке и воспользоваться теоремой 27.10 о сумме вычетов.
Пример 28.2. Вычислить интеграл
Решение. Функция f(z) = имеет восемь особых точек
– решений уравнения z s 4- 1 = 0. Каждая из этих точек Zk является полюсом второго порядка, поскольку в окрестности точки Zk функция f(z) имеет вид f(z) = , где h(z) аналитична в окрестности
точки Zk и h(zk) ф 0. Все особые точки лежат внутри окружности z = 2. Вычисление вычетов во всех этих точках весьма трудоемко. По к данной функции применима теорема 27.10, которая дает
Поэтому достаточно найти вычег в точке zq = эо. Воспользуемся формулой (27.13). Здесь
Функция g(w) представима в виде – 1 ^ ^. где h(w) = ——
Поскольку hi(w) аналитична в окрестности точки wq = 0 и h(0) Ф 0, то вычет reso$ легко найти по формуле (27.6 / ): reso# = h(0) = 1. Из (27.2), (28.1) и (27.13) получаем:
- 2тг
- 2. Вычисление интегралов вида / R(cos ip, sin г . Тогда dz = e tip >
(см. формулы (12.2)). При изменении р от 0 до 2тг точка г описывает окружность z = 1. Поэтому после перехода к переменному 2 мы получим интеграл по единичной окружности от функции, представимой в виде отношения двух многочленов; такие функции называются рациональными дробями или дробно-рациональными функциями.
Пример 28.3. Вычислить интеграл
Решен и е. Выполняя указанные выше подстановки, получим, что данный интеграл равен
Разложим знаменатель на множители, для чего найдем корни уравнения az 2 — (а 2 + )z + а = 0. Дискриминант
Следовательно, подынтегральная функция f(z) имеет две особые точки z — а и 22 = 1/а, каждая из которых является полюсом первого порядка. Так как по условию |а| оо. Пользуясь соотношениями (28.2) и (28.3), получим нужное равенство:
где сумма берется по всем особым точкам из верхней полуплоскости.
Бели полуокружность 7(Я) лежит в нижней полуплоскости, то соответствующий контур Г“ будет обходиться по часовой стрелке (такое направление возникает оттого, что отрезок [—Я, Я] в любом случае должен проходиться слева направо, т.е. в направлении возрастания х). Поэтому в правой части (28.4) добавится знак минус. Теорема 28.4 доказана.
Пример 28.5. Вычислить интеграл
Решение. В данном случае f(z) = ^ + уу • Проверим справедливость условия (28.3):
где h(z) = —-§—ту. Так как lim h(z) = 1, то при достаточно боль-
ших значениях z будет h(z) оо. получим (28.3). Проведепные оценки справедливы как для верхней, так и для нижней полуокружности. Поэтому в качестве 7(Л) можно выбрать любую из них. Пусть у(R) — верхняя полуокружность. Так как
то f(z) имеет две особые точки z — 3г, zo = —Зг, являющиеся полюсами второго порядка. Из них в верхней полуплоскости находится только z = Зг. Вычет в этой точке найдем по формуле (27.7) с тг = 2:
Заметим, что вычислить данный интеграл можно было и не прибегая к методам комплексного анализа, а находя первообразную подынтегральной функции. Но приведенное вычисление значительно проще.
Рассуждение, проведенное нами в примере 28.5 для проверки условия (28.3), без изменения подходит к любой функции f(z), представимой в виде отношения двух многочленов (т.е. рациональной дроби), если степень многочлена в знаменателе на две и более единицы превосходит степень многочлена в числителе. (В примере 28.5 степень многочлена в числителе равна 2, а в знаменателе — 4.) Следующая теорема показывает, что условию (28.3) удовлетворяет и другой важный класс функций, интегралы от которых возникают, например, в операционном исчислении (см. гл. VIII).
Теорема 28.6 (лемма Жордана). Пусть функция F(z) аполитична в полуплоскости lm z ^ —а, за исключением конечного числа изолированных особых точек, и lim F(z) = 0. Если 7(R) — дуга
окружности z = 7?, расположенная в полуплоскости Ini 2 ^ —а, то

Доказательство. Рассмотрим вначале случай а > 0. Обозначим через М(7?) максимум модуля F(z) на дуге 7(7?). Поскольку lira F(z) = 0, то
Разобьем 7(7?) на три части 7i (Л), 72(7?) и 7з(Т?) (рис. 50): дуги 7i(R) и 72(Я) заключены между прямой у = —а и осью ОА", а 7з(Т?) является полуокружностью, лежащей в полуплоскости Im z ^ 0. Очевидно, что интеграл по 7(7?) равен сумме интегралов по этим трем дугам. Оценим каждый из них в отдельности.
В точках z = х + iy дуг 71 (7?) и 72(7?) будет —у и 72(7?) (в радианах). Легко видеть (см. рис. 50), что siny? =
откуда ?>(7?) = arcsin —. Поэтому /(7?) = R

Таким образом, в случае а > 0 теорема доказана. Если а ^ 0, то дуга ‘y(R) лежит в полуплоскости Im z ^ 0 и является частью дуги 73(R); части 7i (R) и 7г(Я) в этом случае отсутствуют. Для 7(R) справедливы рассуждения, проведенные выше для 73(7?), и теорема 28.G полностью доказана.
Смысл теоремы 28.6 состоит в том. что функция F(z) может стремиться к нулю сколь угодно медленно (заметим, что в примере 28.5 убывание функции f(z) при z —? оо было достаточно быстрым как |z|“ 2 ). Но умножение на e ltz обеспечивает стремление интеграла по 7(R) к нулю.
Замечание. Для случая t 0. В случае t — 0 теорема 28.6 неверна.
П р и м е р 28.7. Вычислить интегралы
Таким образом, действительная и мнимая части функции f(x) и являются теми функциями, интегралы от которых нужно найти. Поэтому
ются теми функциями, интегралы от которых нужно найти. Поэтому
- ——- dx и возьмем от него действиям + 9
- — 00
тельную и мнимую части, то получим искомые величины.
Функция F(z) = .Д удовлетворяет условиям теоремы 28.6: она z "f 9
имеет только две особые точки z •> = ±3t и lim —- = 0. Ес-
ли 7(/?) дуга окружности z = R, расположенная в полуплоскости Im z > 0. то согласно tcodcmc 28.6
(мы взяли в (28.5) t = 2). Значит, можно применить теорему 28.4,
согласно которой интеграл / ——- dx равен сумме вычетов функ-
ции f(z) = ——- в особых точках из верхней полуплоскости 1т z > z I J
О, умноженной на 2т. В полуплоскости Im z > 0 лежит единственная
особая точка Z = Зг функции f(z). Так как f(z) = –-—–—,
то z = Зг – полюс первого порядка. Вычет в этой точке можно найти по любой из сЬоомул (27.,’В. (27.6L (27.63. Ппименим (27.63. Злесь
Действительная и мнимая части полученного числа и будут искомыми и I ггегралам и:
(Заметим, что равенство нулю первого из этих интегралов непосредственно следует из того, что он является интегралом от нечетной функции по интервалу, симметричному относительно начала координат.)

































