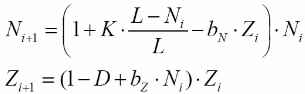Выполните моделирование системы хищник жертва при параметрах

Файлы-заготовки для выполнения этой практической работы

Для выполнения работы откройте файл-заготовку ХищникЖертва.xls.

Выполните моделирование биологической системы «щуки-караси»

где N_i – численность карасей, Z_i – численность щук

при следующих значениях параметров:

K – коэффициент прироста карасей;

L = 100 – предельная численность карасей;

N = 50 – начальная численность карасей;

Z = 10 – начальная численность щук;

D = 0,8 – коэффициент смертности щук без пищи;

Постройте на одном поле графики изменения численности карасей и щук в течение 30 периодов моделирования.

Ответьте на следующие вопросы:

1. Сколько карасей и щук живут в водоеме в состоянии равновесия?

2. Что влияет на количество рыб в состоянии равновесия: начальная численность хищников и жертв или значения коэффициентов модели?

3. На что влияет начальная численность хищников и жертв?

4. Подберите значения коэффициентов, при которых модель становится неадекватна.

5. Подберите значения коэффициентов, при которых щуки вымирают, а численность карасей достигает предельно возможного значения. Как вы можете объяснить это с точки зрения биологии?

физико-математические науки

• Нечипуренко Анна Александровна , студент
• Южный федеральный университет

• Похожие материалы

  Популяционная динамика – один из разделов математического моделирования. Интересен он тем, что имеет конкретные приложения в биологии, экологии, демографии, экономике. В данном разделе имеется несколько базовых моделей, одна из которых – модель «Хищник – жертва» – рассматривается в данной статье.

  Первым примером модели в математической экологии стала модель, предложенная В.Вольтеррой. Именно он впервые рассмотрел модель взаимоотношения между хищником и жертвой.

  Рассмотрим постановку задачи. Пусть имеется два вида животных, один из которых пожирает другой (хищники и жертвы). При этом принимаются следующие предположения: пищевые ресурсы жертвы не ограничены и в связи с этим в отсутствии хищника популяция жертвы возрастает по экспоненциальному закону, в то время как хищники, отделенные от своих жертв, постепенно умирают с голоду так же по экспоненциальному закону. Как только хищники и жертвы начинают обитать в непосредственной близости друг от друга, изменения численности их популяций становятся взаимосвязанными. В этом случае, очевидно, относительный прирост численности жертв будет зависеть от размеров популяции хищников, и наоборот.

  В данной модели считается, что все хищники (и все жертвы) находятся в одинаковых условиях. При этом пищевые ресурсы жертв неограниченны, а хищники питаются исключительно жертвами. Обе популяции живут на ограниченной территории и не взаимодействуют с любыми другими популяциями, также отсутствуют любые другие факторы, способные повлиять на численность популяций.

  Сама математическая модель «хищник – жертва» состоит из пары дифференциальных уравнений, которые описывают динамику популяций хищников и жертв в её простейшем случае, когда имеется одна популяция хищников и одна – жертв. Модель характеризуется колебаниями в размерах обеих популяций, причём пик количества хищников немного отстаёт от пика количества жертв. С данной моделью можно ознакомиться во многих трудах по популяционной динамике или математическому моделированию. Она достаточно широко освещена и проанализирована математическими методами. Однако формулы не всегда могут дать очевидное представление о происходящем процессе.

  Интересно узнать, как именно в данной модели зависит динамика популяций от начальных параметров и насколько это соответствует действительности и здравому смыслу, причём увидеть это графически, не прибегая к сложным расчётам. Для этой цели на основе модели Вольтерра была создана программа в среде Mathcad14.

  Для начала проверим модель на соответствие реальным условиям. Для этого рассмотрим вырожденные случаи, когда в данных условиях обитает только одна из популяций. Теоретически было показано, что при отсутствии хищников популяция жертвы неограниченно возрастает во времени, а популяция хищника в отсутствии жертвы вымирает, что вообще говоря соответствует модели и реальной ситуации (при указанной постановке задачи).

  Полученные результаты отражают теоретические: хищники постепенно вымирают(Рис.1), а численность жертвы неограниченно возрастает(Рис.2).

  

  Рис.1 Зависимость числа хищников от времени при отсутствии жертвы

  

  Рис.2 Зависимость числа жертв от времени при отсутствии хищников

  Как видно, в данных случаях система соответствует математической модели.

  Рассмотрим, как ведёт себя система при различных начальных параметрах. Пусть имеются две популяции – львы и антилопы – хищники и жертвы соответственно, и заданы начальные показатели. Тогда получаем следующие результаты(Рис.3):

  Таблица 1. Коэффициенты колебательного режима системы

  

  Рис.3 Система при значении параметров из Таблицы 1

  Проанализируем полученные данные, исходя из графиков. При первоначальном возрастании популяции антилоп наблюдается прирост числа хищников. Заметим, что пик возрастания популяции хищников наблюдается позже, на спаде популяции жертв, что вполне соответствует реальным представлениям и математической модели. Действительно, рост числа антилоп означает увеличение пищевых ресурсов для львов, что влечёт за собой рост их численности. Далее активное поедание львами антилоп ведёт к стремительному уменьшению численности жертв, что неудивительно, учитывая аппетит хищника, а точнее частоту поедания хищниками жертв. Постепенное снижение численности хищника приводит к ситуации, когда популяция жертвы оказывается в благоприятных для роста условиях. Далее ситуация повторяется с определённым периодом. Делаем вывод, что данные условия не подходят для гармоничного развития особей, так как влекут резкие спады популяции жертв и резкие возрастания обеих популяций.

  Положим теперь начальную численность хищника равную 200 особей при сохранении остальных параметров(Рис.4).

  Таблица 2. Коэффициенты колебательного режима системы

  

  Рис.4 Система при значении параметров из Таблицы 2

  Теперь колебания системы происходят более естественно. При данных предположениях система существует вполне гармонично, отсутствуют резкие возрастания и убывания количества численности в обеих популяциях. Делаем вывод, что при данных параметрах обе популяции развиваются достаточно равномерно для совместного обитания на одной территории.

  Зададим начальную численность хищника равную 100 особей, численность жертв 200 при сохранении остальных параметров(Рис.5).

  Таблица 3. Коэффициенты колебательного режима системы

  

  Рис.5 Система при значении параметров из Таблицы 3

  В данном случае ситуация близка к первой рассмотренной ситуации. Заметим, что при взаимном увеличении популяций переходы от возрастания к убыванию популяции жертвы стали более плавными, а популяция хищника сохраняется в отсутствии жертв при более высоком численном значении. Делаем вывод, что при близком отношении одной популяции к другой их взаимодействие происходит более гармонично, если конкретные начальные численности популяций достаточно большие.

  Рассмотрим изменение других параметров системы. Пусть начальные численности соответствуют второму случаю. Увеличим коэффициент размножения жертв (Рис.6).

  Таблица 4. Коэффициенты колебательного режима системы

  

  Рис.6 Система при значении параметров из Таблицы 4

  Сравним данный результат с результатом, полученным во втором случае. В этом случае наблюдается более быстрый прирост жертвы. При этом и хищник, и жертва ведут себя так, как в первом случае, что объяснялось невысокой численностью популяций. При таком взаимодействии обе популяции достигают пика со значениями, намного большими, чем во втором случае.

  Теперь увеличим коэффициент прироста хищников (Рис.7).

  Таблица 5. Коэффициенты колебательного режима системы

  

  Рис.7 Система при значении параметров из Таблицы 5

  Сравним результаты аналогично. В этом случае общая характеристика системы остаётся прежней, за исключением изменения периода. Как и следовало ожидать, период стал меньше, что объясняется быстрым уменьшением популяции хищника в отсутствии жертв.

  И, наконец, изменим коэффициент межвидового взаимодействия. Для начала увеличим частоту поедания хищниками жертв:

  Таблица 6. Коэффициенты колебательного режима системы

  

  Рис.8 Система при значении параметров из Таблицы 6

  Так как хищник поедают жертву чаще, то максимум численности его популяции увеличился по сравнению со вторым случаем, а также уменьшилась разность между максимальным и минимальным значениями численности популяций. Период колебаний системы остался прежним.

  И теперь уменьшим частоту поедания хищниками жертв:

  Таблица 7. Коэффициенты колебательного режима системы

  

  Рис.9 Система при значении параметров из Таблицы 7

  Теперь хищник поедают жертву реже, максимум численности его популяции уменьшился по сравнению со вторым случаем, а максимум численности популяции жертвы увеличился, причём в 10 раз. Отсюда следует, что при данных условиях популяция жертвы имеет большую свободу в смысле размножения, ведь хищнику хватает меньшей массы, чтобы насытиться. Также уменьшилась разность между максимальным и минимальным значениями численности популяций.

  При попытке моделирования сложных процессов в природе или обществе, так или иначе, возникает вопрос о корректности модели. Естественно, что при моделировании происходит упрощение процесса, пренебрежение некоторыми второстепенными деталями. С другой стороны, существует опасность упростить модель слишком сильно, выкинув при этом вместе с несущественными важные черты явления. Для того чтобы избежать данной ситуации, необходимо перед моделированием изучить предметную область, в которой используется данная модель, исследовать все её характеристики и параметры, а главное, выделить те черты, которые являются наиболее значимыми. Процесс должен иметь естественное описание, интуитивно понятное, совпадающее в основных моментах с теоретической моделью.

  Рассмотренная в данной работе модель обладает рядом существенных недостатков. Например, предположение о неограниченных ресурсах для жертвы, отсутствие сторонних факторов, влияющих на смертность обоих видов и т.д. Все эти предположения не отражают реальную ситуацию. Однако, несмотря на все недостатки, модель получила широкое распространение во многих областях, даже далёких от экологии. Это можно объяснить тем, что система «хищник-жертва» даёт общее представление именно о взаимодействии видов. Взаимодействие с окружающей средой и прочими факторами можно описать другими моделями и анализировать их в совокупности.

  Взаимоотношения типа «хищник-жертва» – существенная черта различных видов жизнедеятельности, в которых происходит столкновение двух взаимодействующих между собой сторон. Данная модель имеет место не только в экологии, но и в экономике, политике и других сферах деятельности. Например, одно из направлений, касающихся экономики, это анализ рынка труда, с учётом имеющихся потенциальных работников и вакантных рабочих мест. Данная тема была бы интересным продолжением работы над моделью «хищник-жертва».

  Электронное периодическое издание зарегистрировано в Федеральной службе по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор), свидетельство о регистрации СМИ — ЭЛ № ФС77-41429 от 23.07.2010 г.

  Соучредители СМИ: Долганов А.А., Майоров Е.В.

  Аннотация научной статьи по математике, автор научной работы — Арзамасцев А. А., Альбицкая Е. Н., Слетков Д. В.

  Discrete stochastic distributed mathematical model describing interaction in the system «beast-victimenvironment » is developed. The mathematical model is object-oriented, i.e. it operates with a certain system of «rules», characteristic for real objects. The model is realized in the form of a program complex in the environment of development Delphi. Computing experiments testify to qualitative conformity of simulation results to both available experimental data and to the results received earlier in classical works, thus developing and supplementing conceptions of the given system.

  Похожие темы научных работ по математике , автор научной работы — Арзамасцев А. А., Альбицкая Е. Н., Слетков Д. В.

  Computer simulation of the system «beast victim» using cellular automatons

  Discrete stochastic distributed mathematical model describing interaction in the system «beast-victimenvironment » is developed. The mathematical model is object-oriented, i.e. it operates with a certain system of «rules», characteristic for real objects. The model is realized in the form of a program complex in the environment of development Delphi. Computing experiments testify to qualitative conformity of simulation results to both available experimental data and to the results received earlier in classical works, thus developing and supplementing conceptions of the given system.

  Текст научной работы на тему «Компьютерное моделирование системы «Хищник жертва» с использованием клеточных автоматов»

  КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ СИСТЕМЫ «ХИЩНИК – ЖЕРТВА» С ИСПОЛЬЗОВАНИЕМ КЛЕТОЧНЫХ АВТОМАТОВ

  © А.А. Арзамасцев, Е.Н. Альбицкая, Д.В. Слетков

  Arzamastsev A.A., Albitskaya E.N., Sletkov D.V. Computer simulation of the system «beast – victim» using cellular automatons. Discrete stochastic distributed mathematical model describing interaction in the system «beast-victim-environment» is developed. The mathematical model is object-oriented, i.e. it operates with a certain system of «rules», characteristic for real objects. The model is realized in the form of a program complex in the environment of development Delphi. Computing experiments testify to qualitative conformity of simulation results to both available experimental data and to the results received earlier in classical works, thus developing and supplementing conceptions of the given system.

  Введение. Попытки количественного описания динамики различных биологических популяций и типов их взаимодействий имеют давнюю историю. Широко известны математические модели, предложенные Т. Мальтусом (Malthus 1798, Мальтус 1905), Фер-хюльстом (Verhulst 1838), Пирлом (Pearl 1927, 1930). Особый интерес для данной статьи представляют результаты теоретических исследований А. Лотки (Lotka 1925, 1927) и В. Вольтерры (Volterra 1926), которые независимо друг от друга предложили модель системы «хищник – жертва», которая воспроизводит периодический колебательный режим, возникающий в результате межвидовых взаимодействий, без какого бы то ни было внешнего периодического воздействия [1]. Экспериментальная проверка данных работ предпринята в исследованиях Г.Ф. Гаузе и его соавторов (Гаузе & Витт 1934, Gause 1934).

  В 1838 г. появилась «логистическая» модель Фер-хюльста (Verhulst 1838), достаточно хорошо описывающая динамику многих природных популяций. Данное уравнение было вновь «переоткрыто» Пирлом (Pearl 1927, 1930). Значительный вклад в популяционную динамику внесли также Станислав Улам, Джон фон Нейман (Ulam, von Neumann 1947), Ли и Йорк (Li, Yorke 1975), Шарковский (Шарковский 1964).

  Следующей крупной вехой в развитии теории экологического моделирования стала работа А.Н. Колмогорова (Колмогоров 1972), в которой было дано глубокое исследование системы «хищник – жертва» при достаточно общих предположениях о характере их взаимодействий. Были сформулированы условия, при которых в системе «хищник – жертва» реализуется устойчивое стационарное состояние или устойчивый предельный цикл. Значительный вклад в развитие теории различных типов популяционных взаимодействий связан также с работами Н.С. Печуркина и И.А. Терскова (Печуркин и Терсков 1975).

  Данный краткий обзор работ, посвященных моделированию взаимодействий в различных биологических системах, позволяет констатировать следующее:

  – существующие модели внесли существенный вклад в формирование теоретической базы для биологических исследований; они позволили объяснить раз-

  личные феномены, наблюдаемые экспериментально (логистический характер кривой роста, колебания численности, наличие аутостабилизации в биологических системах и т. д.);

  – указанные модели являются детерминированными, что приводит к совершенно идентичным результатам вычислительных экспериментов при одинаковых начальных условиях; вместе с тем биологические объекты в значительной степени являются стохастическими;

  – указанные модели представляют собой объекты с сосредоточенными параметрами, что не позволяет использовать их для изучения распределений плотностей популяций биологических видов по территории; данное обстоятельство не позволяет проводить исследования волн численности, миграций по территории и т. д.; кроме того, неравномерность распределения биологических популяций по территории оказывает существенные влияния на динамику развития этих популяций.

  Поэтому в качестве целей данной работы выбраны:

  – разработка стохастической дискретной распределенной модели взаимодействия «хищник – жертва», позволяющей воспроизводить основную феноменологию явления, а также моделировать расположение популяций на территории;

  – проведение с ее помощью вычислительных экспериментов, позволяющих изучить взаимодействия в системе.

  Объект моделирования представляет собой замкнутую среду обитания, в которой происходит взаимодействие двух биологических популяций – хищников и жертв; внутренняя структура объекта включает также комплекс взаимодействий в системах: «хищник – жертва», «среда – хищник», «среда – жертвы». При этом процессы роста, вымирания и размножения популяций происходят на поверхности среды обитания. Питание хищников происходит только за счет жертв. Питание жертв происходит за счет питательных ресурсов среды обитания. При этом питательные ресурсы могут быть как возобновляемыми (непрерывно или периодически), так и невозобновляемыми.

  Выбор в модели дискретного представления объекта обусловлен следующими причинами.

  1. Точное территориальное отображение распределенного объекта в реальных экспериментах невозможно. Например, невозможно точно определить положения отдельных особей на карте в различные моменты времени, поэтому обычно речь идет об осредненных плотностях популяций на определенной территории, что в случае дискретного представления имеет ряд вычислительных преимуществ, незначительно снижая при этом точность моделирования.

  2. Такое представление удобно для моделирования, поскольку клеточные автоматы являются хорошо изученным аппаратом и позволяют применить Agent Based Approach (подход, базируемый на агентах), который начинает широко использоваться в настоящее время для моделирования в биологических, социальных и других недетерминированных системах.

  1. Область среды обитания популяций представляет собой ограниченную часть плоскости с нанесенной дискретной сеткой. Ее можно представить в виде квадратной матрицы, состоящей из ячеек, размером NxN (реально используется 100×100 ячеек, но при необходимости размер матрицы может быть изменен).

  2. Единицей времени в модели является одна итерация; все временные параметры в модели задаются в количестве итераций. Отсчет времени начинается с нуля итераций.

  3. Хищник съедает жертву, находящуюся в одной из соседних ячеек. Жертва питается питательным веществом, расположенным в той же ячейке. Питательные вещества распределены по ячейкам области среды обитания.

  4. Перемещения. На протяжении всей жизни хищник и жертва перемещаются. Перемещение хищника происходит в одну из соседних незанятых ячеек, причем хищник ищет ближайшую по расположению к нему жертву на расстоянии, не превышающем Rhg, и направляется к ней (если таких жертв более одной, он выбирает одну из них случайным образом); если такой жертвы нет, то хищник двигается в случайном направлении. За одну итерацию хищник может делать либо одно, либо два таких перемещения; количество перемещений определяется случайным образом. Перемещение жертвы происходит в одну из соседних незанятых ячеек, при этом жертва находит ближайшего хищника, расположенного на расстоянии, не превышающем Rgh, и удаляется от него; если же такого хищника нет, то жертва ищет ближайшую ячейку, наполненную питательным веществом, и начинает двигаться к ней; если таких ячеек нет, то жертва двигается в случайном направлении. За одну итерацию жертва делает одно такое перемещение. Для каждой особи перемещение осуществляется только в четыре (две по горизонтали и две по вертикали) ближайшие ячейки (см. рис. 1 (1)). Если особь находится на границе области среды обитания, то таких ячеек будет три или две (см. рис. 1 (2) и (3)).

  5. Питательные вещества в модели могут быть заданы либо их определенным количеством в начальный момент времени Q и временем их регенерации Tq , либо их количеством, появляющихся за одну итерацию Q+.

  6. Одна особь занимает одну ячейку области среды обитания.

  7. Потомство. Через определенный промежуток времени хищник и жертва начинают производить потомство, по одному потомку в одну из 4-х соседних ячеек рядом с материнской, если они располагаются во внутренней ячейке, одну из трех или одну из двух ячеек, если они находятся на границе области распространения или в угловой ячейке (рис. 2). Ячейка может быть занята дочерней особью лишь при условии, что в ней нет другой особи. При наличии нескольких свободных ячеек дочерняя особь занимает одну из них, выбранную случайным образом. Если рядом с материнской особью нет свободной ячейки, размножения не происходит. Размножение осуществляется за одну итерацию. Возраст дочерней особи считается с момента деления. Размножение на возрасте материнской особи не сказывается.

  Промежуток времени между размножением особи задается нормальным распределением со средним значением тгк – для хищника и – для жертвы. Время следующего размножения особи определяется в начальный момент времени и после каждого акта размножения.

  Рис. 1. Схема перемещения хищника и жертвы для различных ячеек области обитания: 1 – для особи, находящейся внутри области; 2 – для особи, находящейся на границе области; 3 -для особи, находящейся в угловой клетке области

  Рис. 2. Положения материнской особи (1) и возможные расположения дочерних особей (2)

  8. Максимальная продолжительность жизни особи

  задается нормальным распределением со средним значением т!к – для хищника, – для жертвы. Эти пара-

  метры определяются при образовании среды обитания. Хищник может погибнуть и раньше, если через определенный промежуток времени Тф не находит жертву. Жертва в свою очередь также может погибнуть, если через определенный промежуток времени т№ не находит питательное вещество.

  9. В начальный момент времени хищники располагаются в п ячеек среды обитания, жертвы – в т ячеек. Начальный возраст каждой особи задается также случайным образом, в зависимости от максимальной продолжительности жизни популяции.

  Реализация данной системы допущений в виде алгоритма представляет собой так называемый «клеточный автомат», впервые предложенный в работах [2-4]. Программа модели написана в среде разработки ЭйрЫ. Она представляет собой специализированный симулятор, имеющий удобный графический интерфейс и позволяющий по заданным характеристикам взаимодействия в системах: «хищник – жертва», «среда – хищник», «среда – жертвы» – получать кинетические и морфологические характеристики: количество хищников и жертв во времени, фазовые траектории и их расположение по области среды обитания.

  Вычислительные эксперименты. После того, как математическая модель была протестирована на предмет выявления и устранения в ней разных противоречивых ситуаций, было решено предпринять с ней ряд вычислительных экспериментов.

  Вначале была определена некоторая точка, старт из которой обеспечивал различные сценарии развития системы. Эта точка характеризуется следующими параметрами и начальными условиями для хищников: начальное количество п = 100, среднее время жизни т!к = 2000, среднее время между генерациями тгк = 100, максимальный промежуток жизни без еды Тф = 20, максимальное расстояние, на котором хищник видит жертву Як§ = 20; для жертв: начальное количество т = 1600, среднее время жизни т^ = 1000, среднее время между генерациями т^ = 50, максимальный промежуток жизни без еды т(я = 15, максимальное расстояние, на котором жертва видит хищника Яф = 3; для питательных веществ: количество за итерацию Q+ = 300.

  Все временные показатели здесь и далее выражены в количестве итераций; количественные – показывают число хищников, жертв и «условных» единиц питательной среды; расстояния задаются числом ячеек среды обитания.

  В первой серии вычислительных экспериментов определяли влияние на период получаемого процесса среднего времени генерации хищников. В модели Лотки – Вольтерра установлено, что период таких колебаний зависит от коэффициентов естественного прироста

  следующим образом: т =

  , где £1, £2 – коэффи-

  циенты естественного прироста хищников и жертв.

  Поскольку в нашем случае £1——–, £2——, то в

  данной модели эта формула будет выглядеть следующим образом: Т

  Время между генерациями изменяли в пределах тгк = 30-150 с интервалом Дтгк = 5. Было выявлено, что при малых значениях времени между генерациями хищников происходит полное вымирание популяций хищников и жертв, а графики кривых N0 и N^(1) имеют апериодический характер. Данное обстоятельство объясняется тем, что первоначально численность популяции хищников быстро возрастает, что приводит к исчезновению всех жертв, после чего и сами хищники, лишенные пищи, также погибают. Частный случай такой симуляции представлен на рис. 3.

  Далее, начиная со среднего времени между генерациями хищников тгк = 45 до значения тгк = 130, кривые носят периодический характер, причем видно, что при значениях тгк = 45 – 65 колебания носят практически детерминированный характер, и роль стохастической составляющей крайне незначительна. Это хорошо видно на рис. 4.

  Данное обстоятельство можно связать с тем, что при малом времени между генерациями и при большом числе жертв происходит значительное усреднение, поэтому получаются очень гладкие кривые. Однако со среднего времени между генерациями тгк = 65 роль каждого события существенно возрастает и усреднение происходит значительно хуже. Поэтому периодический характер сохраняется, однако появляется существенная стохастическая составляющая. На рис. 5 показана одна из таких симуляций при тгк = 80.

  При дальнейшем увеличении среднего времени между генерациями роль стохастической составляющей усиливается, что приводит к тому, что периодический характер оказывается утраченным (рис. 6).

  Таким образом, установлен диапазон величин средних значений между генерациями хищника, в котором колебания численности популяций имеют периодический характер, тгк = 45-130.

  На рис. 7 показана зависимость периода колебаний в системе от времени между генерациями хищников, построенная на основе значительного числа вычислительных экспериментов. Из этого рисунка видно, что, несмотря на существенную роль стохастической составляющей, общая тенденция полностью согласуется с представлениями, полученными ранее в модели Лотки – Вольтерра.

  Во второй серии вычислительных экспериментов оценивали влияние среднего времени генерации жертвы на период колебаний в системе.

  Рис. 3. Зависимости числа особей в популяции от модельного времени при: тгк = 30, тгг = 50, т,к = 2000, = 1000, тгк = 20, = 15,