Задача нелинейного программирования графическим методом

В задачах нелинейного программирования целевая функция уже не линейно зависит от переменных, а иным образом (чаще всего встречается квадратичная зависимость – задачи квадратичного программирования), что усложняет задачу и делает невозможным применение стандартных методов (симплекс-метода и его производных).

Тем не менее, в случае 2 переменных по-прежнему используется графический метод, применяются методы множителей Лагранжа, теорема Куна-Таккера, условия стационарности точек. Также разработано множество итерационных методов, которые разобраны ниже на примерах (Зонтендейка, Франка-Вульфа, градиентный, направлений, градиентов Розена, Пауэлла и т.д.)

Методы нелинейного программирования применяются также к задачам составления оптимального портфеля ценных бумаг и задачами управления запасами в случае нескольких типов ресурсов и ограничений на площадь склада.

Вы найдете подробные примеры решений по этой теме – изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении заданий, перейдите в раздел: Контрольные работы по линейному программированию.

Нелинейное программирование: примеры решений

Задача 1. Решить задачу квадратичного программирования методом Зойтендейка. Вычисления вести в натуральных дробях.

$$ max(-6x_1^2-x_2^2+2x_1x_2+10x_2)\ 2x_1+x_2 le 5,\ 2x_1+x_2 ge 2,\ x_1,x_2 ge 0,\ x_0=(0,4). $$

Задача 2. Решить задачу методом Франка-Вульфа (расчеты вести с точностью до 4 знаков после запятой).

$$ max(-x_1^2+x_1x_2 -2x_2^2+4x_1+6x_2)\ x_1+x_2 le 4,\ x_1+2x_2 ge 2,\ x_1,x_2 ge 0,\ x_0=(3,1). $$

Задача 3. Решить задачу методом возможных направлений (расчеты вести с точностью до 4 знаков после запятой).

$$ max(-x_1^2+x_1x_2 -2x_2^2+4x_1+6x_2)\ x_1+x_2 le 4,\ x_1+2x_2 ge 2,\ x_1,x_2 ge 0,\ x_0=(3,1), xi=0,4. $$

Задача 4. Решить задачу нелинейного программирования

$$ min f =x_1^2+2x_2^2-16x_1-20x_2,\ 2x_1+5x_2 le 40,\ 2x_1+x_2 le 16,\ x_1,x_2 ge 0. $$

Задача 5. Используя графический метод, найдите решение задачи нелинейного программирования

$$ F =(x_1-1)^2+(x_2-1)^2 o extr,\ 3x_1+5x_2 le 15,\ 5x_1+3x_2 le 15,\ x_1,x_2 ge 0. $$

Задача 6. Для следующей задачи нелинейного программирования $$ F=3/2x_1^2+1/2x_2^2-x_1x_2-12x_1+2x_2 o min,\ 4x_1+3x_2 ge 12,\ x_1+3x_2le 6,\ x_1,x_2 ge 0. $$ a) доказать, что функция является выпуклой
b) найти минимум целевой функции без учета ограничений с помощью градиентных методов
c) найти минимум целевой функции с учетом ограничений

Задача 7. Решить задачу нелинейного программирования методом проектируемых градиентов Розена

$$ Z=8+8x_1+10x_2-2x_1^2-x_2^2 o max,\ 4x_1+3x_2 le 24,\ x_1+4x_2le 16,\ x_1,x_2 ge 0. $$

Задача 8. Решить задачу безусловной оптимизации методом покоординатного спуска Пауэлла. Выполнить 2 итерации.

$$ F(x)=x_1+4x_2+x_1x_2-2x_1^2-2x_2^2 o max,\ x_1,x_2 in E^2,\ x_0=(-1;4). $$

Задача 9. Используя графический метод, решить следующую задачу квадратического программирования: $$f(x) = 9(x_1-9)^2+9(x_2-9)^2 o min,$$ при ограничениях:

$$ x_1+2x_2ge 2,\ x_1+x_2le 6,\ 2x_1+x_2 le 11,\ x_1,x_2 ge 0. $$

Задача 10. Дана задача выпуклого программирования. Требуется: 1) найти решение графическим методом, 2) написать функцию Лагранжа данной задачи и найти её седловую точку, используя решение задачи, полученное графически:

$$ (x_1-5)^2+(x_2-1)^2 o min,\ 2x_1-x_2ge -4,\ 2x_1-3x_2le -6,\ x_1+x_2 le 11,\ x_1,x_2 ge 0. $$

Чтобы найти ее оптимальное решение, нужно выполнить следующие действия:

Найти ОДР, определяемую ограничениями задачи. Если окажется, что эта область пуста, то это означает, что задача не имеет решения.
Построить семейство линий уровня целевой функции f(х₁, х₂) = C при различных значениях числового параметра С.
При решении задачи на минимум определить направление убывания, а для задачи на максимум — направление возрастания линий уровня ЦФ.
Найти точку ОДР, через которую проходит линия уровня с наименьшим в задаче на минимум (соответственно, наибольшим в задачи на максимум) значением параметра С. Эта точка будет оптимальным решением. Если ЦФ не ограничена снизу в задаче на минимум (сверху — в задаче на максимум), то это означает, что задача не имеет оптимального решения.
Найти координаты точки оптимума и определить в ней значение ЦФ.

Отметим, что в отличие от задачи ЛП точка оптимума в задаче НП не обязательно находится на границе ОДР. Ею также может быть внутренняя точка этого множества.

Пример . В задаче выпуклого программирования требуется:

найти решение графическим методом;
написать функцию Лагранжа и найти ее седловую точку, используя решение, полученное графически.

F(X) = x₁ 2 +(x₂-2) 2
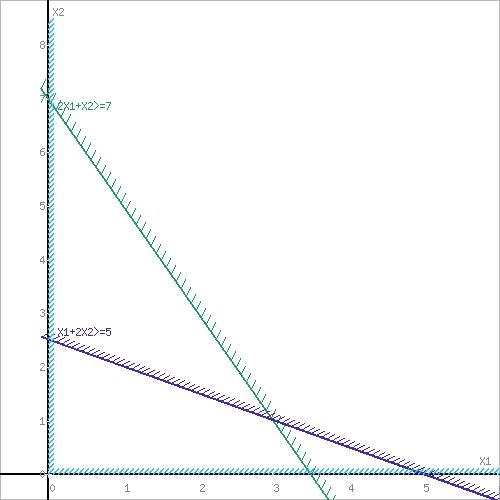
2x₁+x₂ ≥ 7
x₁+2x₂ ≥ 5

Решение. 1) Строим два ограничения, тем самым определяя ОДР. Можно использовать этот калькулятор. Также удобно строить ограничения через этот сервис.

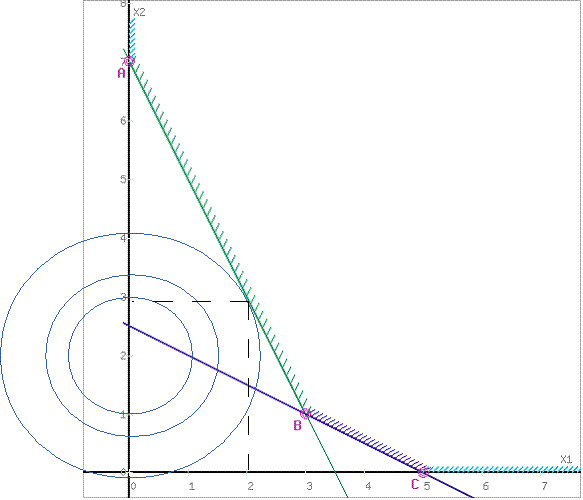
Затем строим функцию цели. В данном случае это окружность.

Поскольку задача минимума, то ищем первое касание линии уровня области ОДР. В данном случае это точка пересечения с прямой 2x₁+x₂-7=0.
Найдем точку пересечения. Для этого построим уравнение касательной, проходящей через центр окружности O(0;2) и перпендикулярно прямой 2x₁+x₂-7=0 (можно использовать этот калькулятор). Получаем: 2x₂-x₁-4=0. Решая систему уравнений:
2x₁+x₂-7=0
2x₂-x₁-4=0,
получаем: x₁=2, x₂=3.

2) Найдем экстремум функции F(X) = x₁ 2 +(x₂-2) 2 , используя калькулятор Функция Лагранжа :
L( X , λ )=F( X )+∑(λ_i·φ_i)
где F( X ) – целевая функция вектора X; φ_i(X) – ограничения в неявном виде (i=1..n)
В качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция: F(X) = x₁ 2 +(x₂-2) 2
Перепишем ограничение задачи в неявном виде:
φ₁(X) = 7 – (2*x₁+x₂) = 0 (X₁)
φ₂(X) = 5 – (x₁+2*x₂) = 0 (X₂)
Составим вспомогательную функцию Лагранжа: L(X, λ) = x₁ 2 +(x₂-2) 2 – λ₁*(7 – (2*x₁+x₂)) – λ₂*(5 – (x₁+2*x₂))
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным х_i и неопределенным множителям λ.
Составим систему:
∂L/∂x₁ = 2*λ₁+λ₂+2*x₁ = 0
∂L/∂x₂ = λ₁+2*λ₂+2*x₂-4 = 0
∂L/∂λ₁ = 2*x₁+x₂-7 = 0
∂L/∂λ₂ = x₁+2*x₂-5 = 0
Решив данную систему, получаем:
а) для случая X₁: x₁ = λ₁/2 + λ₂ + 2; x₂ = 7 – 2x₁
Откуда можно найти такие λ₁ ≥ 0, λ₂ ≥ 0. Пусть λ₂ = 0. Тогда λ₁ = 2; x₁ = 2; x₂ = 3.
Поскольку λ₂ ≥ 0, то данное решение удовлетворяет условиям Куна-Таккера. Z_min(2;3)=5

б) для случая X₂: x₂ = λ₁/2 + λ₂ + 2; x₁ = 5 – 2x₂
Откуда можно найти такие λ₁ ≥ 0, λ₂ ≥ 0. Пусть λ₂ = 0. Тогда λ₁ = 2/5; x₁ = 11/5; x₂ = 3/5.
Поскольку λ₁ ≥ 0, то данное решение удовлетворяет условиям Куна-Таккера. Z_min(11/5;3/5)=6.8

Минимальное значение составит Z_min(2;3)=5.

Найти наибольшее и наименьшее значение функции F = + (x₂ – 4) 2 при ограничениях:

Воспользуемся алгоритмом решения задачи данном в главе I в §4.

Областью допустимых решений задачи является треугольник АВС, который был получен из ограничений системы, путем замены в ограничениях задачи знаков неравенств на знаки точных равенств. Полагая значение целевой функции равное некоторому числу h, получаем линии уровня, а именно окружности + (x₂ – 4) 2 = h с центром в точке Е(3; 4). С увеличением (уменьшением) числа h значения функции F соответственно увеличиваются (уменьшаются).

Проводя из точки Е окружности разных радиусов, видим, что минимальное значение целевая функция принимает в точке D, в которой окружность касается области решений. Для определения координат этой точки воспользуемся равенством угловых коэффициентов прямой 10x₁–х₂ = 8 и касательной к окружности в точке D.

Из уравнения прямой х₂ = 10х₁ – 8 видим, что ее угловой коэффициент в точке D равен 10. Угловой же коэффициент касательной к окружности в точке D определим как значение производной функции х₂ от переменной х₁ в этой точке. Рассматривая х₂ как неявную функцию переменной х₁ и дифференцируя уравнение окружности, получим:

Приравнивая найденное выражение числу 10, получаем одно из уравнений для определения координат точки D. Присоединяя к нему уравнение прямой, на которой лежит точка D, имеем систему:

Решая данную систему получим х₁ = 123/101, х₂ = 422/101. Таким образом F_min = 324/101.

Как видно из рис. 2.1, целевая функция принимает максимальное значение в точке С (2; 12). Ее координаты определены путем решения системы уравнений прямых, на пересечении которых находится точка С. Таким образом, максимальное значение функции F_max =65.

Рис. 2.1. Решение задачи 2.1

Ответ: Минимальное значение целевая функция принимает в точке D(123/101; 422/101) равное F_min = 324/101, а максимальное значение она принимает в точке С(2;12) равное F_max =65.

Найти наибольшее значение функции F = + 4x₂ при ограничениях:

Областью допустимых решений задачи является область АВСЕ, которая была получена из ограничений системы, путем замены в ограничениях задачи знаков неравенств на знаки точных равенств.

Затем строим вектор = (-3; 4) и прямую целевой функции: + 4x₂ = h, проходящую через многоугольник решений.

Передвигая прямую целевой функции вдоль вектора получим максимальное значение в точке В, в которой прямая касается окружности . Для определения координат точки В воспользуемся равенством угловых коэффициентов прямой + 4x₂ = h (где h — некоторая постоянная) и касательной к окружности в точке В. Рассматривая х₂ как неявную функцию переменной х₁, почленно дифференцируем уравнение окружности и получим

Приравнивая найденное выражение числу к = – 3/4, получаем одно из уравнений для определения координат точки В. В качестве второго уравнения возьмем уравнение окружности. Таким образом, для определения координат точки В имеем систему:

Решая данную систему получим х₁ = 4, х₂ =3. Тогда F_max =25.

Рис. 2.2. Решение задачи 2.2

Ответ: максимальное значение целевая функция принимает в точке В(4;3) равное F_max =25.

Найти максимальное значение функции

Областью допустимых решений задачи является многоугольник ABCDE (рис. 2.3). Полагая значение целевой функции F = – x₂ равным некоторому числу h, получим линии уровня, а именно кубические параболы – x₂ = h. С увеличением числа h значения функции F соответственно увеличиваются.

Увеличивая значение h, мы видим, что наша кубическая парабола перемещается вверх по оси ОХ₂, до тех пор пока мы не получим точку К – точку касания кубической параболы и многоугольника решений. В полученной точке К целевая функция принимает максимальное значение.

Для определений координат точки К воспользуемся равенством угловых коэффициентов прямой и касательной к кубической параболе в точке К. Из уравнения прямой мы видим, что ее угловой коэффициент в точке К равен 1,5. Угловой же коэффициент касательной к кубической параболе в точке К, определим как значение производной функции от переменной в этой точке. Рассматривая как неявную функцию переменной и дифференцируя уравнение гиперболы, получим:

Тогда получим систему:

Решая которую с учетом , мы получим = , 3 + . Таким образом,

Рис. 2.3. Решение задачи 2.3

Ответ: = , 3 + . F_max = – 3.

Найти минимальное значение функции

Областью допустимых решений задачи является многоугольник ABCDE (рис. 2.4). Следовательно, для нахождения решения задачи нужно определить такую точку многоугольника ABCDE, в которой функция F = – x₂ принимает минимальное значение. Построим линию уровня F = – x₂ = h, где h — некоторая постоянная, и исследуем ее поведение при различных значениях h. При каждом значении h получаем график логарифмической функции, который при увеличении значения h перемещается вверх вдоль оси ОХ_2. Значит, функция F принимает маинимальное значение в точке касания одной из логарифмических функций с границей многоугольника ABCDE. В данном случае это точка М, в которой линия уровня F = – x₂ касается стороны DC многоугольника ABCDE.

Для определений координат точки М воспользуемся равенством угловых коэффициентов прямой и касательной к логарифмической функции в точке М. Из уравнения прямой мы видим, что ее угловой коэффициент в точке М равен 1. Угловой же коэффициент касательной к логарифмической функции в точке М, определим как значение производной функции от переменной в этой точке. Рассматривая как неявную функцию переменной и дифференцируя уравнение гиперболы, получим:

Тогда получим систему: