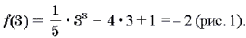Записать уравнение касательной к графику функции

На современном этапе развития образования в качестве одной из основных его задач выступает формирование творчески мыслящей личности. Способность же к творчеству у учащихся может быть развита лишь при условии систематического привлечения их к основам исследовательской деятельности. Фундаментом для применения учащимися своих творческих сил, способностей и дарований являются сформированные полноценные знания и умения. В связи с этим проблема формирования системы базовых знаний и умений по каждой теме школьного курса математики имеет немаловажное значение. При этом полноценные умения должны являться дидактической целью не отдельных задач, а тщательно продуманной их системы. В самом широком смысле под системой понимается совокупность взаимосвязанных взаимодействующих элементов, обладающая целостностью и устойчивой структурой.

Рассмотрим методику обучения учащихся составлению уравнения касательной к графику функции. По существу, все задачи на отыскание уравнения касательной сводятся к необходимости отбора из множества (пучка, семейства) прямых тех из них, которые удовлетворяют определенному требованию – являются касательными к графику некоторой функции. При этом множество прямых, из которого осуществляется отбор, может быть задано двумя способами:

а) точкой, лежащей на плоскости xOy (центральный пучок прямых);
б) угловым коэффициентом (параллельный пучок прямых).

В связи с этим при изучении темы «Касательная к графику функции» с целью вычленения элементов системы нами были выделены два типа задач:

1) задачи на касательную, заданную точкой, через которую она проходит;
2) задачи на касательную, заданную ее угловым коэффициентом.

Обучение решению задач на касательную осуществлялось при помощи алгоритма, предложенного А.Г. Мордковичем [2]. Его принципиальное отличие от уже известных заключается в том, что абсцисса точки касания обозначается буквой a (вместо x0), в связи с чем уравнение касательной приобретает вид

(сравните с y = f(x) + f ‘(x)(x – x)). Этот методический прием, на наш взгляд, позволяет учащимся быстрее и легче осознать, где в общем уравнении касательной записаны координаты текущей точки, а где – точки касания.

Алгоритм составления уравнения касательной к графику функции y = f(x)

1. Обозначить буквой a абсциссу точки касания.
2. Найти f(a).
3. Найти f ‘(x) и f ‘(a).
4. Подставить найденные числа a, f(a), f ‘(a) в общее уравнение касательной y = f(a) = f ‘(a)(x – a).

Этот алгоритм может быть составлен на основе самостоятельного выделения учащимися операций и последовательности их выполнения.

Практика показала, что последовательное решение каждой из ключевых задач при помощи алгоритма позволяет формировать умения написания уравнения касательной к графику функции поэтапно, а шаги алгоритма служат опорными пунктами действий. Данный подход соответствует теории поэтапного формирования умственных действий, разработанной П.Я. Гальпериным и Н.Ф. Талызиной [3].

В первом типе задач были выделены две ключевые задачи:

• касательная проходит через точку, лежащую на кривой (задача 1);
• касательная проходит через точку, не лежащую на кривой (задача 2).

Задача 1. Составьте уравнение касательной к графику функции в точке M(3; – 2).

Решение. Точка M(3; – 2) является точкой касания, так как

1. a = 3 – абсцисса точки касания.
2. f(3) = – 2.
3. f ‘(x) = x 2 – 4, f ‘(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – уравнение касательной.

Задача 2. Напишите уравнения всех касательных к графику функции y = – x 2 – 4x + 2, проходящих через точку M(– 3; 6).

Решение. Точка M(– 3; 6) не является точкой касания, так как f(– 3) ­ 6 (рис. 2).

1. a – абсцисса точки касания.
2. f(a) = – a 2 – 4a + 2.
3. f ‘(x) = – 2x – 4, f ‘(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.

Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0 ^ a₁ = – 4, a₂ = – 2.

Если a = – 4, то уравнение касательной имеет вид y = 4x + 18.

Если a = – 2, то уравнение касательной имеет вид y = 6.

Во втором типе ключевыми задачами будут следующие:

• касательная параллельна некоторой прямой (задача 3);
• касательная проходит под некоторым углом к данной прямой (задача 4).

Задача 3. Напишите уравнения всех касательных к графику функции y = x 3 – 3x 2 + 3, параллельных прямой y = 9x + 1.

1. a – абсцисса точки касания.
2. f(a) = a 3 – 3a 2 + 3.
3. f ‘(x) = 3x 2 – 6x, f ‘(a) = 3a 2 – 6a.

Но, с другой стороны, f ‘(a) = 9 (условие параллельности). Значит, надо решить уравнение 3a 2 – 6a = 9. Его корни a = – 1, a = 3 (рис. 3).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f ‘(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – уравнение касательной;

1) a = 3;
2) f(3) = 3;
3) f ‘(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – уравнение касательной.

Задача 4. Напишите уравнение касательной к графику функции y = 0,5x 2 – 3x + 1, проходящей под углом 45° к прямой y = 0 (рис. 4).

Решение. Из условия f ‘(a) = tg 45° найдем a: a – 3 = 1 ^ a = 4.

1. a = 4 – абсцисса точки касания.
2. f(4) = 8 – 12 + 1 = – 3.
3. f ‘(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – уравнение касательной.

Несложно показать, что решение любой другой задачи сводится к решению одной или нескольких ключевых задач. Рассмотрим в качестве примера следующие две задачи.

1. Напишите уравнения касательных к параболе y = 2x 2 – 5x – 2, если касательные пересекаются под прямым углом и одна из них касается параболы в точке с абсциссой 3 (рис. 5).

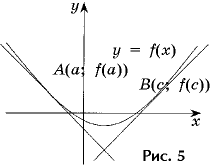
Решение. Поскольку дана абсцисса точки касания, то первая часть решения сводится к ключевой задаче 1.

1. a = 3 – абсцисса точки касания одной из сторон прямого угла.
2. f(3) = 1.
3. f ‘(x) = 4x – 5, f ‘(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – уравнение первой касательной.

Пусть a – угол наклона первой касательной. Так как касательные перпендикулярны, то – угол наклона второй касательной. Из уравнения y = 7x – 20 первой касательной имеем tg a = 7. Найдем

Это значит, что угловой коэффициент второй касательной равен .

Дальнейшее решение сводится к ключевой задаче 3.

Пусть B(c; f(c)) есть точка касания второй прямой, тогда

1. – абсцисса второй точки касания.
2.
3.
4.
– уравнение второй касательной.

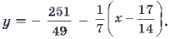
Примечание. Угловой коэффициент касательной может быть найден проще, если учащимся известно соотношение коэффициентов перпендикулярных прямых k₁•k₂ = – 1.

2. Напишите уравнения всех общих касательных к графикам функций

Решение. Задача сводится к отысканию абсцисс точек касания общих касательных, то есть к решению ключевой задачи 1 в общем виде, составлению системы уравнений и последующему ее решению (рис. 6).

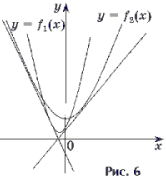
1. Пусть a – абсцисса точки касания, лежащей на графике функции y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f ‘(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 .

1. Пусть c – абсцисса точки касания, лежащей на графике функции
2.
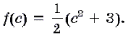
3. f ‘(c) = c.
4.

Так как касательные общие, то

Итак, y = x + 1 и y = – 3x – 3 – общие касательные.

Основная цель рассмотренных задач – подготовить учащихся к самостоятельному распознаванию типа ключевой задачи при решении более сложных задач, требующих определенных исследовательских умений (умения анализировать, сравнивать, обобщать, выдвигать гипотезу и т. д.). К числу таких задач можно отнести любую задачу, в которую ключевая задача входит как составляющая. Рассмотрим в качестве примера задачу (обратную задаче 1) на нахождение функции по семейству ее касательных.

3. При каких b и c прямые y = x и y = – 2x являются касательными к графику функции y = x 2 + bx + c?

Пусть t – абсцисса точки касания прямой y = x с параболой y = x 2 + bx + c; p – абсцисса точки касания прямой y = – 2x с параболой y = x 2 + bx + c. Тогда уравнение касательной y = x примет вид y = (2t + b)x + c – t 2 , а уравнение касательной y = – 2x примет вид y = (2p + b)x + c – p 2 .

Составим и решим систему уравнений

Ответ:

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9469 – | 7452 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Геометрический смысл производной

Ты уже знаешь что такое производная? Если нет, сперва прочти тему «Производная». Итак, ты говоришь, что знаешь производную. Сейчас проверим. Найди приращение функции при приращении аргумента, равном . Справился? Должно получиться . А теперь найди производную функции в точке . Ответ: . Получилось? Если в каком-нибудь из этих примеров возникли сложности, настоятельно рекомендую вернуться к теме «Производная» и проштудировать ее еще раз. Знаю, тема очень большая, но иначе нет смысла идти дальше. Рассмотрим график какой-то функции :

Выберем на линии графика некую точку . Пусть ее абсцисса , тогда ордината равна . Затем выберем близкую к точке точку с абсциссой ; ее ордината – это :

Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии). Обозначим угол наклона прямой к оси как . Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки. Какие значения может принимать угол ? Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – , а минимально возможный – . Значит, . Угол не включается, поскольку положение прямой в этом случае в точности совпадает с , а логичнее выбирать меньший угол. Возьмем на рисунке такую точку , чтобы прямая была параллельна оси абсцисс, а – ординат:

По рисунку видно, что , а . Тогда отношение приращений:

(так как , то – прямоугольный).

Давай теперь уменьшать . Тогда точка будет приближаться к точке . Когда станет бесконечно малым , отношение станет равно производной функции в точке . Что же при этом станет с секущей? Точка будет бесконечно близка к точке , так что их можно будет считать одной и той же точкой. Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки , но этого достаточно). Говорят, что при этом секущая занимает предельное положение.

Угол наклона секущей к оси назовем . Тогда получится, что производная

то есть производная равна тангенсу угла наклона касательной к графику функции в данной точке.

Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:

За что отвечает коэффициент ? За наклон прямой. Он так и называется: угловой коэффициент. Что это значит? А то, что равен он тангенсу угла между прямой и осью ! То есть вот что получается:

Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей? Посмотрим: Теперь углы и тупые. А приращение функции – отрицательное. Снова рассмотрим : . С другой стороны, . Получаем: , то есть все, как и в прошлый раз. Снова устремим точку к точке , и секущая примет предельное положение, то есть превратится в касательную к графику функции в точке . Итак, сформулируем окончательно полученное правило:
Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:

Это и есть геометрический смысл производной. Окей, все это интересно, но зачем оно нам? Вот пример:
На рисунке изображен график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .
Решение.
Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс: . Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной. На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!

Угол наклона касательной к оси – это . Найдем тангенс этого угла: . Таким образом, производная функции в точке равна .
Ответ: . Теперь попробуй сам:

1. На рисунке изображен график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .
2. На рисунке изображен график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .

Ответы:

Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс: . Достроим треугольник со стороной , лежащей на касательной.

Угол наклона касательной – это угол, отмеченный зеленым на графике. Он тупой 90<>^circ
ight)"> , поэтому его тангенс не получится вычислить так же, как в предыдущем примере (ведь в прямоугольном треугольнике не может быть тупого угла). Применим знания из тригонометрии. Интересующий нас угол является смежным с . А значит: Найдем : . Значит тангенс угла наклона касательной (а вместе с ним и значение производной в точке касания) равен .
Ответ: .

Здесь ответ равен . В ЕГЭ такой ответ написать не получится, но мы ведь должны понимать, что математика не ограничена рамками ЕГЭ.

Зная геометрический смысл производной, можно очень просто объяснить правило, что производная в точке локального максимума или минимума равна нулю. Действительно, касательная к графику в этих точках «горизонтальна», то есть параллельна оси абсцисс:
А чему равен угол между параллельными прямыми? Конечно, нулю! А тангенс нуля тоже равен нулю. Вот и производная равна нулю:

Более подробно об этом читай в теме «Монотонность функций. Точки экстремума».

Уравнение касательной

А сейчас сосредоточимся на произвольных касательных. Предположим, у нас есть какая-то функция, например, . Мы нарисовали ее график и хотим провести касательную к нему в какой-нибудь точке . Например, в точке . Берем линейку, пристраиваем ее к графику и чертим:

Что мы знаем об этой прямой? Что самое важное нужно знать о прямой на координатной плоскости? Поскольку прямая – это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты и в уравнении

Но ведь мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке:

В нашем примере будет так:

Теперь остается найти . Это проще простого: ведь – значение при . Графически – это координата пересечения прямой с осью ординат (ведь во всех точках оси ):

Проведём (так, что – прямоугольный). Тогда (тому самому углу между касательной и осью абсцисс). Чему равны и ? По рисунку явно видно, что , а . Тогда получаем:

Соединяем все полученные формулы в уравнение прямой:

Это и есть уравнение касательной к графику функции в точке .

Пример:
Найди уравнение касательной к графику функции в точке .
Решение:
На этом примере выработаем простой алгоритм действий в подобных задачах:

Алгоритм	Пример: ,
1. Вычислим
2. Найдём формулу производной функции
3. Вычислим
4. Подставим и в формулу уравнения касательной

Теперь реши сам:

1. Найди уравнение касательной к функции в точке .
2. Касательная к параболе пересекает ось под углом . Найди уравнение этой касательной.
3. Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания.
4. Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания.
5. Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания.

Решения и ответы:

1. Всё по плану:
2. .
3. .
4. .
5. Поскольку функция на этот раз называется буквой y, то чтобы не запутаться, для касательной введем другую букву: .
6. То, что нам известен угол наклона касательной, очень хорошо: ведь его тангенс равен производной функции, а также угловому коэффициенту касательной. Но тут есть подвох: дело в том, что под углом ось могут пересекать две разные касательные: с наклоном «вправо» и «влево»:
   
   Прямая 2 (та, которая «наклонена влево») с положительным направлением оси составляет угол – это и есть угол наклона прямой к оси . Дальше всё просто: , .
   Прямая 1. , .
   Касательная: .
   Прямая 2. , .
   Касательная: .
   Ответ:; .
7. Абсцисса – это ось , а значит, нам нужно найти значение в точке пересечения касательной и графика функции. Из уравнения мы знаем, что угловой коэффициент наклона касательной равен значению производной в точке касания. Поскольку прямая параллельна касательной, это значит, что их угловые коэффициенты наклона одинаковые .
   
   Согласно правилам вычисления производных, находим производную функции :
   .
   Теперь приравниваем производную к коэффициенту наклона касательной и находим абсциссу точки касания:

   .
   
   Ответ:.

8. Ответ: .
9. Ответ: .

УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ. КРАТКОЕ ОПИСАНИЕ И ОСНОВНЫЕ ФОРМУЛЫ

Геометрический смысл производной

Производная функции в конкретной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или угловому коэффициенту этой касательной:

Уравнение касательной к графику функции в точке :

Алгоритм действий для нахождения уравнения касательной:

Алгоритм	Пример: ,
1. Вычислим
2. Найдем формулу производной функции
3. Вычислим
4. Подставим и в формулу уравнения касательной

P.S. ПОСЛЕДНИЙ БЕСЦЕННЫЙ СОВЕТ 🙂

Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.

Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!

Теперь самое главное.

Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.

Проблема в том, что этого может не хватить…

Для успешной сдачи ОГЭ или ЕГЭ, для перехода в 10-й класс или поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.

Я не буду тебя ни в чем убеждать, просто скажу одну вещь…

Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.

Но и это – не главное.

Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю.

Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?

НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.

На экзамене у тебя не будут спрашивать теорию.

Тебе нужно будет решать задачи на время.

И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.

Это как в спорте – нужно много раз повторить, чтобы выиграть наверняка.

Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!

Я рекомендую использовать для этих целей наш учебник "YouClever" (который ты сейчас читаешь, но без ограничений) и решебник и программу подготовки "100gia".

Условия их приобретения изложены здесь: кликните по этой ссылке, приобретите доступ к YouClever и 100gia и начните готовиться прямо сейчас!

И в заключение.

Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.

“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.

Найди задачи и решай!

Комментарии

Спасибо. Всё понятно и красиво оформлено. Но в пункте 3 таблицы по нахождению уравнения касательной допущена ошибка. Значение производной в точке Хо = 6, а не 8.

Пусть дана функция f , которая в некоторой имеет конечную Тогда прямая, проходящая через точку имеющая угловой коэффициент называется .

А что будет, если производная не существует? Возможны два варианта:

1. Касательная к графику тоже не существует. Классический пример — функция в точке (0; 0).
2. Касательная становится вертикальной. Это верно, к примеру, для функции

Уравнение касательной

Всякая невертикальная прямая задается уравнением вида угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой достаточно знать значение функции и производной в этой точке.

Итак, пусть дана функция которая имеет производную на отрезке Тогда в любой точке к графику этой функции можно провести касательную, которая задается уравнением:

Здесь f ’( x ) — значение производной значение самой функции.

Задача. Дана функция y = x 3 . Составить уравнение касательной к графику этой функции

Уравнение касательной: нам дана, а вот значения придется вычислять.

Для начала найдем значение функции. Тут все легко:
Теперь найдем производную:
Подставляем в производную
Итого получаем:
Это и есть уравнение касательной.

Задача. Составить уравнение касательной к графику функции

В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:

f ( x ) = f ( π /2) = 2sin ( π /2) + 5 = 2 + 5 = 7;
f ’( x ) = (2sin x + 5)’ = 2cos x ;
f ’( x ) = f ’( π /2) = 2cos ( π /2) = 0;

y = 0 · ( x − π /2) + 7 ⇒ y = 7

В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.