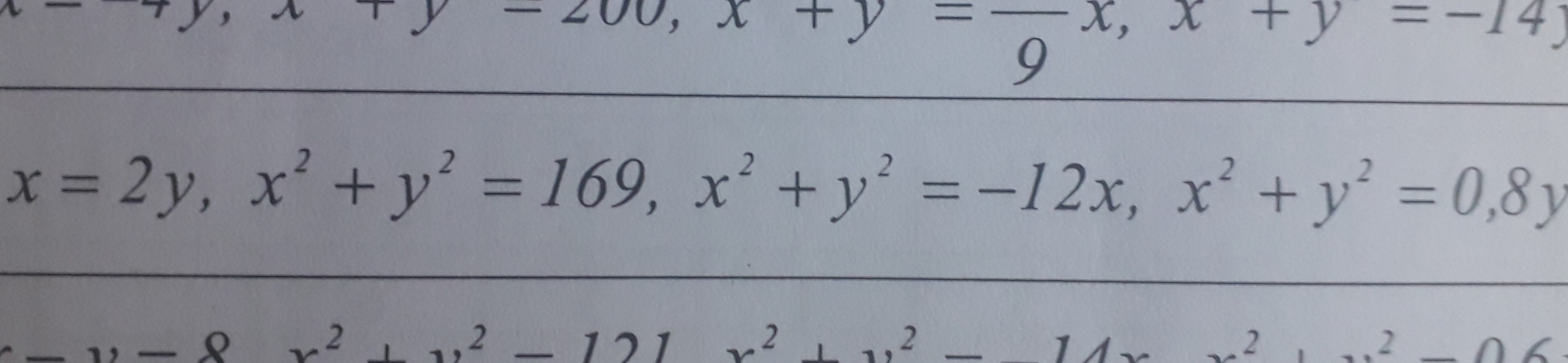Записать уравнение линии в полярных координатах

Ранее мы рассматривали уравнения линий в декартовых координатах, но аналогично можно говорить и об уравнениях линий в полярных координатах. Уравнением линии в полярной системе координат мы будем называть такое уравнение между переменными которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют

координаты точек, не принадлежащих ей. Рассмотрим пример на нахождение уравнении данной линии в полярных координатах.

Пусть требуется найти уравнение окружности, проходящей через полюс, центр которой С лежит на полярной оси, а радиус равен а. Соединим отрезками прямой произвольную точку М окружности с полюсом и с конечной точкой D диаметра, проходящего через полюс (рис. 32). Координатами точки М будут угол и длина отрезка ОМ. Припомним, что окружность есть геометрическое место вершин прямых углов, опирающихся на ее диаметр. Следовательно, треугольник OMD — прямоугольный.

Это и есть искомое уравнение окружности.

Заметим, что вид уравнения данной линии зависит от выбора полюса и полярной оси. Так, если мы выберем полюс в центре окружности радиуса а, то для всех точек окружности (и только для этих точек) полярный радиус будет иметь одно и то же значение это равенство будет, следовательно, уравнением окружности радиуса а с центром в полюсе. Полярный угол в это уравнение не входит, оставаясь произвольным.

При исследовании формы линии на основании ее уравнения приходится часто пользоваться полярными координатами. Это удобно делать всякий раз, когда уравнение линии в полярных координатах проще, чем в декартовых. В качестве примеров мы рассмотрим две линии, часто встречающиеся в приложениях.

Пример 1. Линия, называемая спиралью Архимеда, определяется в полярных координатах уравнением

где а есть положительная постоянная. Чтобы начертить эту линию, будем давать произвольные значения и определять соответствующие значения . Приводимая таблица значений удовлетворяющих данному уравнению, показывает, что при возрастании угла в арифметической прогрессии с разностью полярный радиус возрастает тоже в арифметической прогрессии с разностью . Кроме того, заметим, что всякой точке этой линии с положительными координатами соответствует на этой же линии точка

т. е. спираль Архимеда расположена симметрично относительно прямой, проходящей через полюс перпендикулярно к полярной оси. На рис. 33 сплошной линией изображена ветвь, соответствующая положительным значениям а пунктирной — отрицательным.

Пример 2. Линия, определяемая в полярных координатах уравнением

где а и k суть положительные постоянные, называется логарифмической спиралью.

Чтобы начертить эту линию, будем давать произвольные значения и определять соответствующие значения . Приводимая здесь таблица значений удовлетворяющих данному уравнению, показывает, что при возрастании угла в арифметической прогрессии с разностью полярный радиус возрастает в геометрической прогрессии со знаменателем Когда угол неограниченно возрастает, то тоже неограниченно растет; когда угол Ф стремится к отрицательной бесконечности, то полярный радиус стремится к нулю и кривая неограниченно приближается к полюсу О, закручиваясь около него.

Поэтому точка О называется асимптотической точкой логарифмической спирали (рис. 34).

Иногда встречается надобность в переходе от уравнения линии в декартовых коврдннатах к уравнению той же линии в полярных координатах или обратно. В таком случае следует применять формулы, связывающие полярные и декартовы координаты (гл. 1, § 11).

Пример. Уравнение окружности в полярных координатах

записать в декартовых координатах.

Выражаем через

Подставляя эти выражения в данное уравнение, после упрощений получим:

1. Построить кривую, заданную уравнением (Эта кривая носит название локона Аньези.)

2. Построить кривую, заданную уравнением (Эта кривая называв] четырехлепестковой розой.)

3. Построить кривые, заданные уравнениями:

4. Построить кривые, которым в полярных координатах соответствуют уравнения:

5. Построить кривые, заданные в полярных координатах уравнениями:

6. Составить уравнение геометрического места точек, одинаково удаленных от начала координат и от точки

7. Составить уравнение геометрического места точек, одинаково удаленных от оси Ох и от точки Построить кривую.

8. Определить траекторию точки М, которая движется так, что ее расстояние от точки остается вдвое меньше расстояния от точки

9. Определить траекторию точки М, которая движется так, что ее расстояние от точки остается вдвое меньше расстояния прямой

10. Найти уравнение геометрического места точек, произведение расстояний которых до двух данных точек Р и Q есть величина постоянная, оавиая Расстояние между Р и Q равно (Это геометрическое место точек называется овалом Кассини.) Построить эту линию.

11. Овал Кассини (см. упражнение 10) для случая, когда , называется лемнискатой Бернулли. Найти уравнение лемнискаты: а) в декартовых координатах и б) в полярных координатах. Построй эту кривую.

12. Даны прямая Ох и на расстоянии а от нее точка А (рис. 35). Если прямая будет вращаться около точки А, то точки лежащие на этой прямой и отстоящие от точки В пересечения прямой АВ с основной прямой Ох на данное расстояние b, опишут некоторую линию. Она называется конхоидой Никомеда. Найти уравнение конхоиды и построить ее для случаев

13. Даны прямая Оу и точка А на расстоянии а от нее (рис. 36). Вокруг точки А вращается луч А В и на нем в обе стороны от точки В (точки пересечения луча с осью Оу) отложены переменные отрезки ВМ, и равные по длине ОВ. При вращении луча АВ точки М, и описывают кривую, называемую строфоидой. Составить уравнение этой кривой построить ее.

14. Даны окружность диаметра и касательная к ней РЕ (рис. 37). Через точку О, диаметрально противоположную точки D, проведен луч ОЕ и на нем отложен отрезок ОР, равный отрезку BE, заключающемуся между окружностью и касательной.

Если луч ОЕ будет вращаться около точки О, то точка Р опишет кривую, называемую циссоидой Диоклеса. Найти уравнение этой кривой и построить ее.

15. Даны окружность радиуса а и на ней точка О (рис. 38). Если прямая О В будет вращаться около тчки О, то точки М, и находящиеся на данной прямой и отстоящие на данное расстояние от точки В пересечения прямой с окружностью, опишут кривую, называемую улиткой Паскаля. Найти уравнение этой кривой в полярных координатах и построить ее. (Кривые вычертить для случаев )

16. Составить уравнение геометрического места точек, равноудаленных от двух данных точек.

17. Две прямые вращаются вокруг двух неподвижных точек, оставаясь все время перпендикулярными друг к Другу. Найги уравнение линии, описываемой точкой их пересечения.

18. Из точки М проведены к двум окружностям радиусов R и две равные касательные. Найти уравнение геометрического места точек М при условии, что расстояние между центрами окружностей равно

19. Отрезок постоянной длины 2а скользит своими концами по сторонам прямого угла. Из вершины прямого угла на этот отрезок опущен перпендикуляр ОМ. Найти уравнение геометрического места оснований этих перпендикуляров в полярных координатах и построить эту линию.

20. Найтн геометрическое место точек, сумма квадратов расстояний которых от сторон квадрата равьа постоянной величине.

21. Написать уравнение циссоиды в полярных координатах.

22. Нанисать уравнения кривых:

а) (улитка Паскаля);

б) (четырехлепестковая роза) в декартовых координатах.

23. Круг радиуса а катится без скольжения по оси абсцисс. Найти параметрические уравнения линии, описываемой при указанном движении той точкой окружности, которая при начальном положении окружности находилась в начале координат.

24. Тело брошено вверх со скоростью v под углом а к горизонту. Найти, пренебрегая сопротивлением воздуха, параметрические уравнения траектории тела (за параметр принять время).

По существу, уравнение линии в полярной системе координат представляет собой функцию полярного радиуса от полярного угла (аргумента). При этом полярный угол учитывается в радианах и непрерывно принимает значения от 0 до (иногда следует рассмотреть до бесконечности, или же в ряде задач для удобства от до ). Каждому значению угла «фи», которое входит в область определения функции , соответствует единственное значение полярного радиуса.

Примером полярной кривой является Архимедова спираль . На следующем рисунке изображен её первый виток – когда полярный радиус вслед за полярным углом принимает значения от 0 до :

Одна из ветвей спирали Архимеда, задаваемая уравнением для .Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:

Изменения параметра приводят к повороту спирали, а параметра — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для а другую для . Две ветви плавно соединяются в полюсе. Зеркальное отображение одной ветви относительно прямой, проходящей через угол 90°/270°, даст другую ветвь. Эта кривая интересна тем, что была описана в математической литературе одной из первых, после конического сечения, и лучше других определяется именно полярным уравнением.

Круг, заданный уравнением .

Общее уравнение окружности с центром в () и радиусом имеет вид:

Это уравнение может быть упрощено для частных случаев, например является уравнением, определяющим окружность с центром в полюсе и радиусом . [14]

Радиальные прямые (те, которые проходят через полюс) определяются уравнением где — угол, на который прямая отклоняется от полярной оси, то есть, где — наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую в точке определяется уравнением

Полярная роза задана уравнением

Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах: для произвольной постоянной (включая 0). Если — целое число, то это уравнение будет определять розу с лепестками для нечётных , либо с лепестками для чётных . Если — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Если — иррациональное, то роза состоит из бесконечного множества частично накладывающихся друг на друга лепестков. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная определяет длину лепестков.

Если считать, что радиус не может быть отрицательным, то при любом натуральном мы будем иметь -лепестковую розу. Таким образом, уравнение будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.

– является частным случаем полярной розы.

Трехлепестковая роза задается уравнением

Коническое сечение, один из полюсов которого находится в полюсе, а другой где-то на полярной оси (так, что малая полуось лежит вдоль полярной оси) задаётся уравнением:

где — эксцентриситет, а — фокальный параметр. Если , это уравнение определяет гиперболу; если , то параболу; если , то эллипс. Отдельным случаем является , определяющее окружность с радиусом .

Лемнискамта (от лат. lemniscatus — «украшенный лентами») — плоская алгебраическая кривая порядка , у которой произведение расстояний от каждой точки до заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами.

Рассмотрим простейший случай: если расстояние между фокусами равняется , расположены они на оси , и начало координат делит отрезок между ними пополам, то следующие уравнения задают лемнискату:

· в прямоугольных координатах:

Проведя несложные преобразования, можно получить явное уравнение:

· в полярных координатах:

-плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом [1] . Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.

Кардиоида является частным случаем улитки Паскаля, эпициклоиды и синусоидальной спирали.

Пусть – радиус окружностей, начало координат находится в крайней правой точке горизонтального диаметра неподвижной окружности. Тогда уравнения кардиоиды можно записать в следующих формах:

В прямоугольных координатах:

В прямоугольных координатах (параметрическая запись):

В полярных координатах [2][1] :

(от греч. буфспн — звезда и ейдпт — вид, то есть звездообразная) [1] — плоская кривая, описываемая точкой окружности радиуса r, катящейся по внутренней стороне окружности радиуса . Иначе говоря, астроида — это гипоциклоида с модулем k =4.

Уравнение в декартовых прямоугольных координатах:

Астроида также является алгебраической кривой рода 1 (и шестого порядка). Уравнение в алгебраическом виде:

Пример 2.3.Составить уравнение прямой линии в полярных координатах.

Поместим полюс полярной системы координат в начало прямоугольной системы координат, полярную ось совместим с положительной полуосью абсцисс (см. рис. 17).

Возьмем уравнение прямой в нормальном виде

Формулы перехода имеют вид

Подставив в это уравнение значения x и y из формулы (2.1), получим ,или, откуда , и окончательно .

В этом уравнении постоянными величинами являются p и , величины же r и – переменные: это текущие полярные координаты точки на прямой (последняя формула может быть получена также из чертежа).

Пример 2.4. Построить кривую r = a cos 2ц и найти ее уравнение в прямоугольной системе координат.

Будем давать значения полярному углу от до через промежуток и вычислим соответствующие значения r. Найденные значения поместим в таблицу. Примем произвольный отрезок за единицу масштаба, которой будем пользоваться при построении r. По значениямr и из таблицы построим точки, соответствующие каждой паре чисел r и , и соединим их плавной кривой.

• – a

Построение кривой показано на следующих рисунках:

На рисунке кривые, построенные на различных этапах, соединены в одну. Полученная кривая называется четырехлепестковой розой.

Теперь найдем уравнение четырехлепесковой розы в прямоугольной системе координат, причем напоминаем, что начало прямоугольной системы координат помещено в полюс полярной системы координат, а ось абсцисс направлена вдоль полярной оси.

Учитывая, что , уравнение четырехлепестковой розы перепишем в виде . Подставляя сюда формулы перехода

Возводя обе части последнего уравнения в квадрат, получим окончательно

Пример 2.5. Линия задана уравнением в полярной системе координат.

1) построить линию по точкам начиная с до и придавая значения через промежуток ;

• 2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
• 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

Построим линию по точкам, предварительно заполнив таблицу значений r и :

Используя данные таблицы, строим линию:

Найдем уравнение данной линии в декартовой системе координат:

УСЛОВИЕ:

Записать уравнения кривых в полярных координатах и построить их.

РЕШЕНИЕ ОТ sova ✪ ЛУЧШЕЕ РЕШЕНИЕ

Вводим полярные координаты
x=r*cos φ
y=r*sin φ

1)
x=2y
r*cos φ=2r*sinφ ⇒ tgφ=2 – уравнение линии в полярных координатах

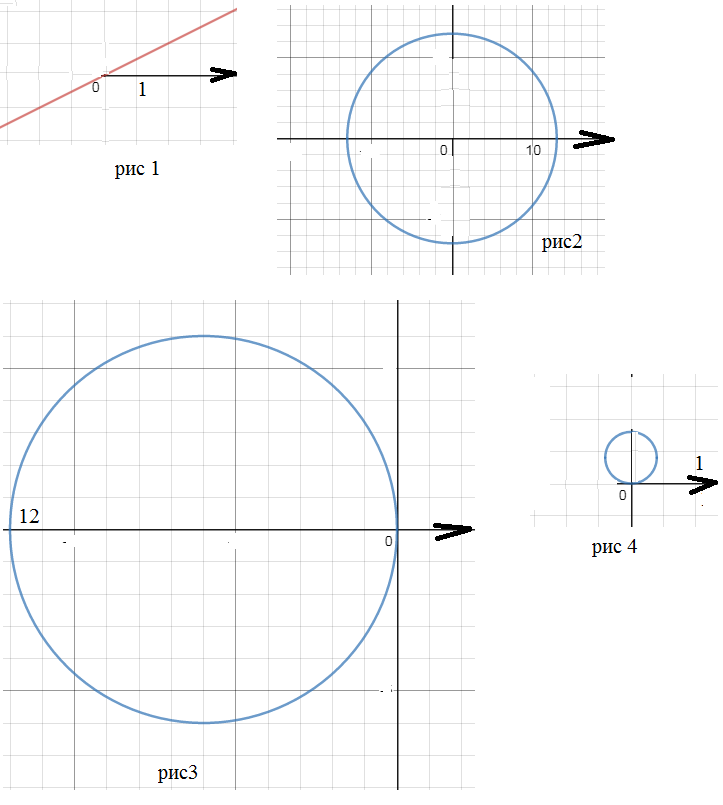
Луч под углом φ к полярной оси, причем tgφ =2

(r*cos φ)^2+(r*sinx φ)^2=169

r^2*(cos^2 φ +sin^2 φ )=13

r=13 – уравнение линии в полярных координатаx

Окружность с центром в точке О радиусом r=13

(r*cos φ)^2+(r*sinx φ)^2=-12*r*cosφ

r^2*(cos^2 φ +sin^2 φ )=-12*r*cosφ

так как r ≥ 0 ⇒ -12cosφ ≥ 0 ⇒ cos φ ≤ 0

Окружность в 2 и 3 четверти

(r*cos φ)^2+(r*sinx φ)^2=0,8*r*sinφ

r^2*(cos^2 φ +sin^2 φ )=0,8*rsinφ

так как r ≥ 0 ⇒ 0,8*sinφ ≥ 0 ⇒ sin φ ≥ 0

Окружность в 1 и 2 четверти

Добавил vasyuk88 , просмотры: ☺ 729 ⌚ 2019-05-31 11:43:55. предмет не задан класс не задан класс

Решения пользователей

Написать комментарий

1.
Смотрим на пределы интегрирования
У первого интеграла:
y=0; y=1
x=0; x=sqrt(y)
Получаем область D_(1)

У второго интеграла:
y=1; y=2
x=0; x=sqrt(2-y)

Получаем область D_(2)

Общая область на рис. 3

Вертикальные полосы: x=0; x=1 – это и есть пределы интегрирования по переменной х

У линий x=sqrt(y) и x=sqrt(2-y)
выразим у через х
y=x^2 и y=2-x^2

О т в е т. ∫^(1)_(0)dx ∫ ^(2-x^2)_(x^2) f(x;y)dy

2.
Область на рис. 4

0 (прикреплено изображение)

((y-1)^2/2)-((x+3)^2/(4/3))=1 – гипербола, центр в точке (-3; 1)

большая полуось – на оси, параллельной оси Оу
равна b= sqrt(2)
малая полуось – на оси, параллельной оси Ох
равна a= sqrt(4/3)

x=-(1/2)(y+4)^2-2 – парабола вдоль оси Ох

ветви в направлении противоположном направлению оси Ох
Вершина в точке (-4;-2)

Искомая плоскость проходит через oсь Oy, значит проходит через начало координат.
Пусть уравнение искомой плоскости

У плоскости x+sqrt(6)y-z-3=0 нормальный вектор vector=(1;sqrt(6);-1)

У плоскости Ax+By+Cz=0 нормальный вектор vector=(A;B;C)

Угол между плоскостями равен углу между их нормальными векторами
По формуле:
cos( ∠ (vector, vector))=(vector* vector)/|vector|*| vector|

Так как по условию угол между плоскостями равен 60 градусов
значит
cos 60 градусов =1/2

где vector* vector – скалярное произведение.

Ось Оу содержит направляющий вектор vector=(0;1:0)

Значит, искомая плоскость проходит через точку (0;1:0)

Из двух уравнений относительно А, В, С и D находим

Возводим в квадрат

A^2-2A*C+C^2=2A^2+2C^2 ⇒ A^2+2AC+C^2=0
A=-C