Случайным событием (просто событием) называется любой факт, который в результате может произойти или не произойти.
Испытание – это выполнение определенного комплекса условий, в котором наблюдается то или иное явление, фиксируется тот или иной факт.
Обозначение: А,В,С и т.д.
Соб.А – выигрыш авто по билету лотереи
Соб.В – появление герба при подбрасывании монеты.
Случай называется благоприятствующим событию А, если появление этого случая влечет за собой появление события А.
Два события А и В называются несовместными, если наступление одного исключает появление другого. (Пример: соб.А – студент получил 5 на экзамене, соб.В – этот же студент получил 4 по этому же предмету. Соб.А и В несовместные, т.к. не могут произойти при одном исходе испытаний.)
Два события А и В называются совместными, если они могут произойти при одном исходе испытаний. (Студент получил 5 по одному предмету и 4 по другому)
Событие называется достоверным, если в результате испытания оно обязательно должно произойти.
Событие называется невозможным, если в результате испытания оно вообще не может произойти. (Пример: в партии изделия все стандартные. Соб.А – извлечение стандартного изделия, соб.В – извлечение брака. А – достоверное, В – невозможное)
События называются равновозможными, если в результате испытания по условиям симметрии не одно из этих событий не является объективно более возможным.(Пример: пусть происходит подбрасывание монеты. Соб.А- орел, соб.В – решка)
Несколько событий называются единственно возможными, если в результате испытания обязательно должно произойти хотя бы одно из них.
События образуют полную группу, если они являются единственно возможными и несовместными исходами испытания.
Два несовместных события, из которых одно должно произойти называются противоположными.
Обозначение: А, 
Вероятностное пространство опыта: множество всех событий, связанных с опытом, как множество всех подмножеств пространства элементарных исходов. Два типа классификации событий: по возможности наступления и по составу.
Вероятностное пространство — это тройка 
— это произвольное множество, элементы которого называются элементарными событиями, исходами или точками;
— сигма-алгебра подмножеств
, называемых (случайными) событиями;
— вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что
.
- Элементарные события (элементы
), по определению, — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один.
- Каждое случайное событие (элемент
) — это подмножество
. Говорят, что в результате эксперимента произошло случайное событие
, если (элементарный) исход эксперимента является элементом
.
Требование, чтоявляется сигма-алгеброй подмножеств
, позволяет, в частности, говорить о вероятности случайного события, являющегося объединением счетного числа случайных событий, а также о вероятности дополнения любого события.
Таким образом, множество всех событий, связанных с опытом – это множество всех подмножеств пространства элементарных исходов.
События (по возможности наступления) делятся на:
· Невозможные (в результате опыта никогда не произойдут),
· Достоверные (в результате опыта происходят всегда),
· Случайные (в результате опыта событие может произойти или непроизойти).
События называются равновозможными, если в результате испытания по условиям симметрии не одно из этих событий не является объективно более возможным.(Пример: пусть происходит подбрасывание монеты. Соб.А- орел, соб.В – решка)
Несколько событий называются единственно возможными, если в результате испытания обязательно должно произойти хотя бы одно из них.
События образуют полную группу, если они являются единственно возможными и несовместными исходами испытания.
Два несовместных события, из которых одно должно произойти называются противоположными.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9467 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Теорема сложения вероятностей. Теорема умножения вероятностей.
Составитель преподаватель кафедры высшей математики Ищанов Т.Р.
Тeория. Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же опыте; в противном случае события называются совместными.
Пример 1. При бросании игральной кости выпадение 3 очков и 6 очков события несовместные, так как они одновременно не могут произойти в одном и том же опыте.
Пример 2. А — появление четырех очков при бросании игральной кости; В-появление четного числа очков. События А и В совместные, так появление одного из них не исключает появление другого в одном и том же испытании.
Два события называются независимыми, если вероятность появления одного из них не влияет на вероятность появления другого события, в противном случае события зависимы.
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А – деталь годная, В – деталь окрашенная, то АВ – деталь годна и окрашена. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С – появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то «АВС» – выпадение «герба» во всех трех испытаниях.
Условной вероятностью 
px;"> 
Пример 3. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).
Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность
px;"> 
Этот же результат можно получить по формуле
px;"> 
Действительно, вероятность появления белого шара при первом испытании
px;"> 
Найдем вероятность Р (АВ) того, что в первом испытании появится черный шар, а во втором—белый. Общее число исходов — совместного появления двух шаров, безразлично какого цвета, равно числу размещений
px;"> 
Из этого числа исходов событию AВ благоприятствуют 
px;"> 
Искомая условная вероятность
px;"> 
Как видим, получен прежний результат.
Теорема умножения вероятностей (для зависимых событий). Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
px;"> 
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
px;"> 
где 
В частности, для трех событий 
Пример 4. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков — конусный, а второй — эллиптический.
Решение. Вероятность того, что первый валик окажется конусным (событие А), 
Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик— конусный, т. е. условная вероятность 
По теореме умножения, искомая вероятность
px;"> 
Пример 5. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар (событие А), при втором — черный (событие В) и при третьем—синий (событие С).
Решение. Вероятность появления белого шара в первом испытании 
Вероятность появления черного шара во втором испытании, вычисленная в предположении, что в первом испытании появился белый шар, т. е. условная вероятность 
Вероятность появления синего шара в третьем испытании, вычисленная в предположении, что в первом испытании появился белый шар, а во втором — черный, т. е. условная вероятность 
px;"> 
Теорема умножения вероятностей (для независимых событий). Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
px;"> 
Суммой А+В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А – попадание при первом выстреле, В – попадание при втором выстреле, то А+В – попадание при первом выстреле, или при втором, или в обоих выстрелах. В частности, если два события А и В – несовместные, то А+В – событие, состоящее в появлении одного из этих событий, безразлично какого. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.
Теорема сложения вероятностей (для несовместных событий). Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
px;"> 
Пример 6. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
Решение Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного шара (событие A) P (A) = 10/30 = 1/3. Вероятность появления синего шара (событие B) P (B) = 5/30 = 1/6. События A и B несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима. Искомая вероятность P (A + B) = P (A) + P (B) = 1/3 + 1/6 = 0,5.
Пример 7. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую – 0,35.Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.
Решение. Событие A – «стрелок попал в первую область» и B – «стрелок попал во вторую область» — несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима. Искомая вероятность P (A + B) = P (A) + P (B) = 0,45 + 0,35 = 0,80.
Теорема сложения вероятностей (для совместных событий). Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
px;"> 
Для трех событий A, B, C имеем:
px;"> 
Замечание 1. При использовании полученной формулы следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми. Для независимых событий:
px;"> 
Пример 8. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: p1 = 0,7; p2 = 0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.
Решение. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А (попадание первого орудия) и В (попадание второго орудия) независимы. Вероятность события АВ (оба орудия дали попадание) Р (АВ)=Р (А)*Р(В) = 0,7*0,8 = 0,56. Искомая вероятность Р(А+В)=Р(А) + Р(В)—Р(АВ) = 0,7 + 0,8 — 0,56=0,94.
Замечание. Так как в настоящем примере события А и В независимые, то можно было воспользоваться формулой 
px;"> 
Искомая вероятность того, что при одном залпе хотя бы одно орудие даст попадание, равна 
Для зависимых событий: 
Вероятность появления хотя бы одного события.
Теорема. Вероятность появления хотя бы одного из событий A1, A2, . An, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 
px;"> 
Частный случай. Если события 
px;"> 
Практический материал.
1.(6.4.12) В урне 4 белых и 3 черных шара. Из нее вынимают 2 шара. Найти вероятность того, что оба шара белые. Рассмотреть выборки: а) без возвращения; б) с возвращением.
2. Вероятность наступления некоторого случайного события в каждом опыте одинакова и равна 0,2. Опыты проводятся последовательно до наступления этого события. Определить вероятность того, что: а) придется проводить четвертый опыт; б) будет проведено четыре опыта. Ответ: а) P (A)=0,8 3 ; б) P (B)=0,8 3 ·0,2
3. Три стрелка одновременно стреляют по одной мишени. Вероятности попадания при одном выстреле соответственно равны 0,7; 0,8 и 0,9. Найти вероятности того, что при одновременном залпе этих стрелков в мишени будет: а) только одно попадание; б) хотя бы одно попадание. Ответ: а) 0,092; б) 0,994
4. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8. (Указание: Задача обратная примеру 8). Ответ: 0,7
5. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное. Ответ: 0,18
6. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность. Ответ: 0,432
Два соб-я наз-ся несовместимыми, если 1 соб-е исключает появление другого. Неск-ко соб-ий наз-ся попарно несовместимыми, если появл-е любого из этих соб-ий исключает появление других.
Сложение вероятностей зависит от совместности и несовместности событий.
Несовместные события. Вер-ть суммы двух несовм соб А и В равна сумме вер-ей этих соб-й. Это вытекает из того, что множество С = А+В включает подмножества А и В, не имеющие общих точек, и Р(А+В) = Р(А)+Р(В) по опр вер-ти на основе меры. По частотному опр-ю вер-ти в силу несовместности соб-й имеем: P(A+B) = 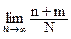

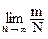
Противоположные события также являются несовместными и образуют полную группу. Отсюда, с учетом: P( 
Совместные события. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
P(A+B) = P(A) + P(B) – P(A×B).
Разобьем события А и В каждое на два множества, не имеющие общих точек: А’, A” и B’, B”. Во множества А” и B” выделим события, появляющиеся одновременно, и объединим эти множества в одно множество С. Для этих множеств действительны выражения:
С = A”×B” º А” º В” º А×В, P(C) = P(A”) = P(B”) = P(A×B).
Множества A’, B’ и С попарно несовм : P(A+B) = P(A’+B’+C) = P(A’) + P(B’) + P(С).
В общем случае, для m различных событий А1, А2, . Аm:
P(A1+. + Am) = 

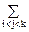
Теорема сложения: Вер-ть суммы двух несовм-х соб-й = сумме вер-тей этих соб. P(A+B+…+К)=P(A)+P(B)+…+Р(К)
Доказательство:Пусть в рез-те испытания из общего числа n равновозможных и несовм-х исходов испытания соб-ю А благоприятствует m1 случаев, а соб-ю В – m2 случаев. Согласно классич определению P(A)=m1
, P(В)=m2
. Т.к соб А и В несовм-е, то ни 1 из случаев, благоприят-х 1 из этих соб-й, не благоприят-т другому. Поэтому событию А+В будет благоприятств-ть m1+m2 случаев, следовательно:
Следствие 1:Сумма вер-ей событий, образующих полную группу, равна 1: P(A)+P(B)+…+Р(К)=1, Если события А,В,…,К образуют полную группу, то они единственно возможные и несовместимые.
ТК событияА,В,…,К – единственно возможные, то событие А+В+…+К, состоящее в появлении в рез-те испытания хотя бы одного из этих событий, явл-ся достоверным, его вер-ть = 1 : Р(А+В+…+К)=1В силу тч события А,В,…,К – несовместимые, к ним применима теорема сложения: Р(А+В+…+К)=Р(А)+Р(В)+…+Р(К)=1
Следствие 2: Сумма вер-ей противоположных событий = 1 Р(А)+Р(`А )=1Это следует из тч противоположные события образуют полную группу.
Пример 1. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара. Решение. Появление цветного шара означает появление либо красного, либо синего шара.
Вероятность появления красного шара (событие А) Р (А) = 10 / 30 = 1 / 3. Вероятность появления синего шара (событие В) Р (В) = 5 / 30 = 1 / 6. События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима. Искомая вероятность P (A + B) = P (A) + P (B) = l / 3 + l / 6 = l / 2.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10579 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
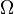 — это произвольное множество, элементы которого называются элементарными событиями, исходами или точками;
— это произвольное множество, элементы которого называются элементарными событиями, исходами или точками;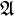 — сигма-алгебра подмножеств
— сигма-алгебра подмножеств  — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что
— вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что  .
. , если (элементарный) исход эксперимента является элементом
, если (элементарный) исход эксперимента является элементом  .
.