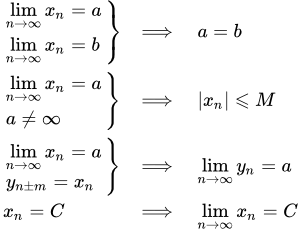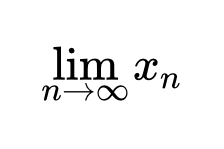Содержание
- 1 Свойства и теоремы
- 2 Доказательство свойств и теорем
- 2.1 Доказательство свойства окрестности сходящейся последовательности
- 2.2 Доказательство свойства окрестности последовательности, не сходящейся к числу a
- 2.3 Доказательство теоремы единственности предела числовой последовательности
- 2.4 Доказательство теоремы об ограниченности последовательности, имеющей конечный предел
- 2.5 Доказательство свойства последовательности из постоянных элементов
- 2.6 Доказательство свойства о влиянии конечного числа элементов на сходимость
- 3 Определение последовательности
- 4 Определение предела последовательности
- 5 Свойства конечных пределов последовательностей
- 6 Бесконечно большая и бесконечно малая последовательности
- 7 Критерии сходимости последовательностей
- 8 Подпоследовательности
Экзамен по матану.
Модуль 1: Элементарные функции и пределы.
Числовая последовательность. Предел последовательности; сходящейся и расходящейся последовательности. Теорема о единственности предела сходящейся последовательности (с доказательством).
Последовательностью называется любой счётный набор действительных чисел а1, а2, а3,…, аn,….
| 1). 1, 1, 1,…,1,…; аn=1, nÎN; | 3). 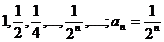 ; nÎN; ; nÎN; |
2). 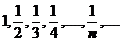 ; аn= ; аn= 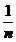 , nÎN; , nÎN; |
4). 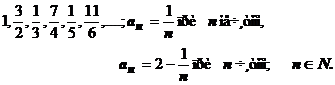 |
Число а называется пределом последовательности 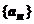
Теор.Последовательность может иметь не более одного предела.
Док-во. От противного: предположим, что последовательность имеет два предела: 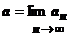
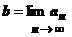
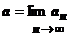
Ограниченная числовая последовательность. Теорема об ограниченности сходящейся числовой последовательности. Признак Вейерштрасса сходимости монотонной последовательности (формулировка).
Если последовательность сходится, то она ограничена.
Док-во. Пусть $ 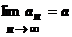
Определение по Коши конечного и бесконечного предела функции в точке и на бесконечности. Односторонние пределы функции. Определение предела функции по Гейне. Теорема о связи двустороннего предела функции в точке с односторонними пределами (с доказательством).
(Коши) Пусть а – предельная точка области определения Х функции f(x). Число b называется пределом функции при х, стремящемся к а, если для любого числа e>0 существует такое число d (вообще говоря, положительное и зависящее от e), что если хÎХ принадлежит также проколотой d-окрестности 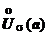
Обозначения: 
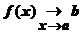
Краткая форма записи: 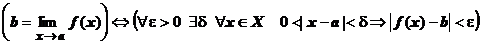
Односторонние пределы функции.
Опр. Число b называется пределом функции f(x) при х®а справа (или правым, правосторонним пределом), если для любого числа e>0 существует такое число d, что если хÎХ удовлетворяет неравенству a 0 существует такое число d, что если хÎХ удовлетворяет неравенству a-d 0 существует такое число K, что если хÎХ удовлетворяет неравенству x>K, то | f(x)-b |
Обозначения: 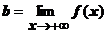
Опр. Число b называется пределом функции f(x) при х®-µ, если для любого числа e>0 существует такое число K, что если хÎХ удовлетворяет неравенству x
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10074 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Свойства и теоремы
Свойство окрестности сходящейся последовательности
Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.
Доказательство ⇓
Свойство окрестности последовательности, не сходящейся к числу a
Если число a не является пределом последовательности , то существует такая окрестность точки a , за пределами которой находится бесконечное число элементов последовательности.
Доказательство ⇓
Теорема единственности предела числовой последовательности
Если последовательность имеет предел, то он единственный.
Доказательство ⇓
Теорема об ограниченности последовательности, имеющей конечный предел
Если последовательность имеет конечный предел, то она ограничена.
Доказательство ⇓
Свойство последовательности из постоянных элементов
Если каждый элемент последовательности равен одному и тому же числу C : , то эта последовательность имеет предел, и этот предел равен числу C .
Доказательство ⇓
Влияние конечного числа элементов на сходимость
Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.
Доказательство ⇓
Доказательство свойств и теорем
При доказательстве свойств, мы будем использовать определение предела последовательности:
.
Доказательство свойства окрестности сходящейся последовательности
Пусть точка a является пределом последовательности . Согласно определению предела последовательности это означает, что для любой окрестности точки a существует такое натуральное число N, что все элементы последовательности с номерами принадлежат этой окрестности. (см. «Эквивалентное определение предела последовательности»).
Тогда первые N элементов последовательности могут находиться где угодно. То есть за пределами окрестность могут находиться не более N элементов последовательности – конечное число или пустое множество.
Первая часть доказана.
Пусть теперь за пределами любой окрестности точки a находится конечное число элементов последовательности или пустое множество. Пусть N есть наибольший номер элемента, находящегося за пределами окрестности. Тогда все элементы последовательности с номерами принадлежат этой окрестности. Это означает, что точка a является пределом последовательности.
Доказательство свойства окрестности последовательности, не сходящейся к числу a
Допустим противное. Пусть число a не является пределом последовательности и за пределами любой окрестности точки a находится только конечное число элементов последовательности. Рассмотрим произвольную окрестность точки a . Пусть N есть наибольший номер элемента, находящегося за ее пределами. Тогда все элементы с номерами принадлежат окрестности. Но это означает, что число a является пределом последовательности, что противоречит предположению.
Свойство доказано.
Доказательство теоремы единственности предела числовой последовательности
Предположим противное, что у последовательности существует два различных предела:
и . Причем .
Поскольку, по предположению, существует предел , то это означает, что имеется функция . Так что при , для любого , выполняется неравенство . То есть элементы последовательности, при , находятся в интервале
(1.1) .
Точно также, поскольку существует предел , то имеется функция . Так что при , для любого , выполняется неравенство . Тогда при , элементы последовательности находятся в интервале
(1.2) .
Возьмем . То есть ε равно половине длины отрезка ab . При таком выборе, интервалы (1.1) и (1.2) не имеют общих точек.
Пусть N – наибольшее из чисел и . Тогда для всех , должны выполняться соотношения (1.1) и (1.2). То есть элементы последовательности, при , должны находиться и в интервале (1.1) и в интервале (1.2). Возникает противоречие, поскольку эти интервалы не имеют общих точек.
Мы взяли . Для доказательства можно было взять другие значения и , для которых интервалы (1.1) и (1.2) не имеют общих точек.
Доказательство теоремы об ограниченности последовательности, имеющей конечный предел
Пусть последовательность имеет конечный предел a :
.
Это означает, что имеется функция такая, что при , для любого , выполняется неравенство
(2.1) .
Возьмем любое значение ε . Например, . Тогда, в силу (2.1), элементы последовательности с номерами , находятся в пределах интервала
(2.2) .
Элементы последовательности, с номерами , могут находиться за пределами интервала (2.2). Но их конечное число. Поэтому их значения ограничены некоторыми числами и . То есть, при , элементы последовательности ограничены интервалом
(2.3) .
В качестве и можно взять значения наименьшего и наибольшего элемента при .
Итак, при , элементы последовательности ограничены неравенствами (2.3), а при – неравенствами (2.2). Тогда для любого n , выполняются следующие неравенства:
(2.4) ,
где есть наименьшее из чисел и ; – наибольшее из чисел и .
Неравенства (2.4) означают, что последовательность ограничена снизу значением , и сверху – значением , или просто ограничена. Что и требовалось доказать.
Также ограниченность элементов можно записать одним неравенством:
,
где M есть наибольшее из чисел и .
Доказательство свойства последовательности из постоянных элементов
В случае последовательности с равными элементами, какую бы ε – окрестность точки C мы не взяли, все элементы этой последовательности будут находиться в этой окрестности:
.
Действительно, подставив сюда , имеем:
;
,
что выполняется для всех n , поскольку .
Тогда в качестве функции мы можем взять любую постоянную, не зависящую от ε , например .
Тогда для любого положительного числа существует такое число , что для всех натуральных выполняется неравенство
.
Это и означает, что число C является пределом последовательности .
Доказательство свойства о влиянии конечного числа элементов на сходимость
Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.
Хотя здесь мы рассматриваем только конечные пределы, но доказательство этой теоремы повторяется один в один, если включить в рассмотрение и бесконечные пределы. Поэтому рядом с формулами, применимыми только для конечных пределов, мы будем приводить универсальные формулы, пригодные как для конечных, так и для бесконечных пределов. Их мы будем помечать звездочкой. При первом чтении раздела их можно пропустить.
Пусть мы имеем последовательность , которая имеет конечный предел
.
Это означает, что имеется такая функция , что для любого , элементы последовательности с номерами , находятся в ε – окрестности числа a :
(3.1) .
В более общем случае, когда a может быть также одной из бесконечно удаленных точек: или , вместо (3.1) следует записать следующее:
(3.1*) ,
где обозначает ε – окрестность точки a .
Рассмотрим последовательность , которая получается из , добавлением первых m элементов. То есть
(3.2)
и есть произвольные числа при .
Покажем, что . Для этого нам нужно найти такую функцию , что для любого , элементы последовательности с номерами , находятся в интервале:
(3.3) ;
(3.3*) .
Подставим в (3.1) и прибавим к обеим частям второго неравенства m :
;
* .
Заменим n + m на k :
;
* .
Эти неравенства совпадают с (3.3), если положить и обозначить индекс k буквой n . Поэтому число a является пределом последовательности .
Теперь рассмотрим последовательность , которая получается из , удалением первых m элементов. То есть
(3.4) .
Покажем, что . То есть нам нужно найти такую функцию , что для любого , элементы последовательности с номерами , находятся в интервале
(3.5) ;
(3.5*) .
Для этого преобразуем неравенства (3.1) ⇑. Заметим, что функция определена не однозначно. Ее всегда можно увеличить на любое натуральное число. То есть вместо (3.1) можно записать так:
(3.1.1) ;
(3.1.1*) .
Действительно, поскольку , то из неравенства следует неравенство .
Подставим в (3.1.1) n = k + m :
;
* .
Подставим (3.4) и преобразуем:
;
* .
Эти неравенства совпадают с (3.5), если положить и обозначить индекс k буквой n . Поэтому число a является пределом последовательности .
Итак, мы доказали, что если число a является пределом последовательности при , то число a также является пределом расширенной последовательности и усеченной последовательности .
Пусть теперь число a не является пределом последовательности . Докажем, что это число также не является пределом последовательности . Допустим противное, что число a является пределом последовательности . Но последовательность получается из последовательности удалением первых элементов. Поэтому, как мы только что доказали, последовательность должна иметь предел a . Возникает противоречие. Поэтому число a не может быть пределом последовательности . Точно так же, если число a не является пределом последовательности , то оно не является и пределом последовательности .
Тем самым мы доказали, что добавление или удаление первых элементов не влияет на сходимость последовательности. Докажем, что изменение первых m элементов также не влияет на сходимость. Для доказательства удалим первые m элементов у исходной последовательности. Получим промежуточную последовательность, сходимость которой такая же, как у исходной. Затем добавим в промежуточную последовательность первые m элементов с произвольными значениями. Получим последовательность, у которой, по отношению к исходной, изменены первые m элементов. Сходимость такой последовательности такая же как и у промежуточной, а поэтому такая же как и у исходной.
Автор: Олег Одинцов . Опубликовано: 29-07-2017 Изменено: 18-02-2019
Определение последовательности
Более подробно см. страницу Определение числовой последовательности >>>.
Далее мы будем считать, что элементами последовательности являются действительные числа.
Последовательность называется ограниченной, если существует такое число M , что для всех действительных n .
Верхней гранью последовательности называют наименьшее из чисел, ограничивающее последовательность сверху. То есть это такое число s , для которого для всех n и для любого , найдется такой элемент последовательности , превосходящий s′ : .
Нижней гранью последовательности называют наибольшее из чисел, ограничивающее последовательность снизу. То есть это такое число i , для которого для всех n и для любого , найдется такой элемент последовательности , меньший i′ : .
Верхнюю грань также называют точной верхней границей, а нижнюю грань – точной нижней границей. Понятия верхней и нижней граней справедливы не только к последовательностям, но и к любым множествам действительных чисел.
Определение предела последовательности
С помощью логических символов существования и всеобщности определение предела можно записать следующим образом:
.
ε – окрестность точки a – это открытый интервал ( a – ε, a + ε ) . Сходящаяся последовательность – это последовательность, у которой существует предел .
Также говорят, что последовательность сходится к a . Расходящаяся последовательность – это последовательность, не имеющая предела.
Точка a не является пределом последовательности , если существует такое , что для любого натурального n существует такое натуральное m > n , что
.
.
Это означает, что можно выбрать такую ε – окрестностью точки a , за пределами которой будет находиться бесконечное число элементов последовательности.
Свойства конечных пределов последовательностей
Основные свойства
Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.
Если число a не является пределом последовательности , то существует такая окрестность точки a , за пределами которой находится бесконечное число элементов последовательности.
Теорема единственности предела числовой последовательности. Если последовательность имеет предел, то он единственный.
Если последовательность имеет конечный предел, то она ограничена.
Если каждый элемент последовательности равен одному и тому же числу C : , то эта последовательность имеет предел, равный числу C .
Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.
Арифметические действия с пределами
Пусть существуют конечные пределы и последовательностей и . И пусть C – постоянная, то есть заданное число. Тогда
;
;
;
, если .
В случае частного предполагается, что для всех n .
Свойства, связанные с неравенствами
Если и элементы последовательности, начиная с некоторого номера, удовлетворяют неравенству , то и предел a этой последовательности удовлетворяет неравенству .
Если и элементы последовательности, начиная с некоторого номера, принадлежат замкнутому интервалу (сегменту) , то и предел a также принадлежит этому интервалу: .
Если и и элементы последовательностей, начиная с некоторого номера, удовлетворяют неравенству , то .
Если и, начиная с некоторого номера, , то .
В частности, если, начиная с некоторого номера, , то
если , то ;
если , то .
Пусть и . Если a b , то найдется такое натуральное число N , что для всех n > N выполняется неравенство .
Бесконечно большая и бесконечно малая последовательности
Бесконечно малая последовательность
Сумма и разность конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.
Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Для того, чтобы последовательность имела предел a , необходимо и достаточно, чтобы , где – бесконечно малая последовательность.
Доказательства свойств бесконечно малых последовательностей приведены на странице
Бесконечно малые последовательности – определение и свойства >>>.
Бесконечно большая последовательность
Бесконечно большая последовательность – это последовательность, имеющая бесконечно большой предел. То есть если для любого положительного числа существует такое натуральное число N , зависящее от , что для всех натуральных выполняется неравенство
.
В этом случае пишут
.
Или при .
Говорят, что стремится к бесконечности.
Если , начиная с некоторого номера N , то
.
Если же , то
.
Если последовательность являются бесконечно большой, то, начиная с некоторого номера N , определена последовательность , которая является бесконечно малой. Если являются бесконечно малой последовательностью с отличными от нуля элементами, то последовательность является бесконечно большой.
Если последовательность бесконечно большая, а последовательность ограничена, то
.
Если абсолютные значения элементов последовательности ограничены снизу положительным числом ( ), а – бесконечно малая с неравными нулю элементами, то
.
Более подробно определение бесконечно большой последовательности с примерами приводится на странице
Определение бесконечно большой последовательности >>>.
Доказательства свойств бесконечно больших последовательностей приведены на странице
Свойства бесконечно больших последовательностей >>>.
Критерии сходимости последовательностей
Монотонные последовательности
Аналогичными неравенствами определяются другие монотонные последовательности.
Строго убывающая последовательность:
.
Неубывающая последовательность:
.
Невозрастающая последовательность:
.
Отсюда следует, что строго возрастающая последовательность также является неубывающей. Строго убывающая последовательность также является невозрастающей.
Монотонная последовательность – это неубывающая или невозрастающая последовательность.
Монотонная последовательность ограничена, по крайней мере, с одной стороны значением . Неубывающая последовательность ограничена снизу: . Невозрастающая последовательность ограничена сверху: .
Теорема Вейерштрасса. Для того чтобы неубывающая (невозрастающая) последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной сверху (снизу ). Здесь M – некоторое число.
Поскольку любая неубывающая (невозрастающая) последовательность ограничена снизу (сверху), то теорему Вейерштрасса можно перефразировать следующим образом:
Для того чтобы монотонная последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной: .
Монотонная неограниченная последовательность имеет бесконечный предел, равный для неубывающей и для невозрастающей последовательности.
Критерий Коши сходимости последовательности
Условие Коши
Последовательность удовлетворяет условию Коши, если для любого существует такое натуральное число , что для всех натуральных чисел n и m , удовлетворяющих условию , выполняется неравенство
.
Фундаментальная последовательность – это последовательность, удовлетворяющая условию Коши.
Критерий Коши сходимости последовательности. Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она удовлетворяла условию Коши.
Доказательство критерия сходимости Коши приведено на странице
Критерий Коши сходимости последовательности >>>.
Подпоследовательности
Теорема Больцано – Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность. А из любой неограниченной последовательности – бесконечно большую подпоследовательность, сходящуюся к или к .
Доказательство теоремы Больцано – Вейерштрасса приведено на странице
Теорема Больцано – Вейерштрасса >>>.
Определения, теоремы и свойства подпоследовательностей и частичных пределов рассмотрены на странице
Подпоследовательности и частичные пределы последовательностей>>>.
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
В.А. Зорич. Математический анализ. Часть 1. Москва, 1997.
В.А. Ильин, Э.Г. Позняк. Основы математического анализа. Часть 1. Москва, 2005.
Автор: Олег Одинцов . Опубликовано: 09-07-2017 Изменено: 30-12-2018