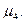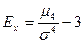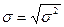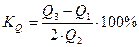При анализе вариационных рядов смещение от центра и крутизну распределения характеризуют специальные показатели. Эмпирические распределения, как правило, смещены от центра распределения вправо или влево, асимметричны. Нормальное распределение строго симметрично относительно средней арифметической, что обусловлено четностью функции.
Асимметрия распределения возникает вследствие того, что какие-либо факторы действуют в одном направлении сильнее, чем в другом, или процесс развития явления таков, что доминирует какая-то причина. Кроме того, природа некоторых явлений такова, что имеет место асимметричное распределение.
Наиболее простой мерой асимметрии является разность между средней арифметической, модой и медианой:
– в симметричном ряду: 
– при правосторонней асимметрии: Мо Ме > 
Для определения направления и величины смещения (асимметрии) распределения рассчитывается коэффициент асимметрии, представляющий собой нормированный момент третьего порядка:
As = m3/s 3 , где m3 – центральный момент третьего порядка; s 3 – среднее квадратическое отклонение в кубе. m3 = (m3 – 3m1 m2 + 2m1 3 )k 3 .
При левосторонней асимметрии коэффициент асимметрии (As 0) .
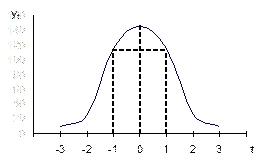
Если вершина распределения сдвинута влево и правая часть ветви оказывается длиннее левой, то такая асимметрия является правосторонней, в противоположном случае левосторонней .
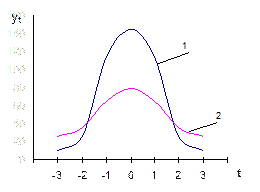
| Рис. Асимметрия распределения: а – правосторонняя; б – левосторонняя | Рис. Характеристика распределений в соответствии с эксцессом: 1 – высоковершинное; 2 – нормальное; 3 – низковершинное |
Соотношение между модой, медианой и средней арифметической в симметричном и асимметричном рядах позволяет в качестве меры асимметрии использовать более простой показатель коэффициента асимметрии Пирсона:
Кa = (
Ex = (m4/s 4 ) – 3, где: m 4 – центральный момент четвертого порядка.
Для нормального распределения Ех = 0, т.е. m4/s 4 = 3. m4 = (m4 – 4m3 m1 + 6m2 m 2 1 – 3 m 4 1)*k 4 .
У высоковершинных кривых эксцесс положительный, у низковершинных отрицательный (рис. Г.2).
Показатели эксцесса и асимметрии необходимы в статистическом анализе для определения неоднородности совокупности, асимметричности распределения и близости эмпирического распределения к нормальному закону. При значительных отклонениях показателей асимметрии и эксцесса от нуля нельзя признать совокупность однородной, а распределение близким к нормальному. Сопоставление фактических кривых с теоретическими позволяет математически обосновать полученные статистические результаты, установить тип и характер распределения социально-экономических явлений, прогнозировать вероятность появления изучаемых событий.
Обоснование близости эмпирического (фактического) распределения к теоретическому нормальному распределению. Нормальное распределение (закон Гаусса-Лапласа) и его характеристики. «Правило трех сигм». Критерии согласия (на примере критерия Пирсона или Колгомогорова).
Можно заметить определенную связь в изменении частот и значений варьирующего признака. Частоты с ростом значения признака сначала увеличиваются, а затем после достижения какой-то максимальной величины уменьшаются. Такие закономерные изменения частот в вариационных рядах называются закономерностями распределения.
Для выявления закономерности распределения необходимо, чтобы вариационный ряд содержал достаточно большое количество единиц, а сами ряды представляли собой качественно однородные совокупности.
Построенный по фактическим данным полигон распределения – это эмпирическая (фактическая) кривая распределения, отражающая не только объективные (общие), но и субъективные (случайные) условия распределения, не характерные для изучаемого явления.
В практической работе закон распределения находят путем сравнения эмпирического распределения с одним из теоретических и оценки степени различия или соответствия между ними. Теоретическая кривая распределения отражает в чистом виде, без учета влияния случайных факторов, общую закономерность распределения частот (плотности распределения) в зависимости от значений варьирующих признаков.
В статистике распространены различные виды теоретических распределений: нормальное, биномиальное, Пуассона и др. Каждое из теоретических распределений имеет свою специфику и область применения.
Закон нормального распределения характерен для распределения равновероятных событий, происходящих при взаимодействии множества случайных факторов. Закон нормального распределения лежит в основе статистических методов оценки параметров распределения, репрезентативности выборочных наблюдений, измерения взаимосвязи массовых явлений.
Для проверки, насколько фактическое распределение соответствует нормальному, необходимо сравнить частоты фактического распределения с теоретическими частотами, характерными для нормального закона распределения. Эти частоты являются функцией нормированных отклонений. Поэтому по данным эмпирического ряда распределения вычисляют нормированные отклонения t. Затем определяют соответствующие им теоретические частоты. Таким образом, выравнивается эмпирическое распределение.
Нормальное распределение или закон Гаусса-Лапласа описывается уравнением 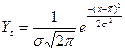



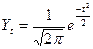
Нормальное распределение характеризуется двумя существенными параметрами, определяющими центр группирования индивидуальных значений и форму кривой: средней арифметической 


-3s -2s -s 
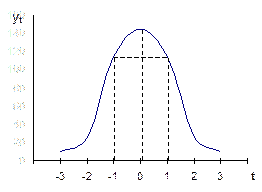
| Рис. Г.3. Нормальное распределение | Рис. Г.4. Нормальное распределение с различными дисперсиями (s1 2 2 ) |
Кривая нормального распределения имеет две точки перегиба (переход от выпуклости к вогнутости) при t = ±1, т.е. при отклонении вариантов от средней (х – 



Для расчета теоретических частот применяется формула:

Величина 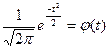
Таблица 9.1. Значения плотности нормального распределения
| t | j(t) | t | j(t) | t | j(t) | t | j(t) |
| 0,0 0,2 0,4 0,6 0,8 | 0,3989 0,3910 0,3683 0,3332 0,2897 | 1,0 1,2 1,4 1,6 1,8 | 0,2420 0,1942 0,1497 0,1109 0,0790 | 2,0 2,2 2,4 2,6 2,8 | 0,0540 0,0355 0,0224 0,0136 0,0079 | 3,0 3,2 3,4 3,6 3,8 | 0,0044 0,0024 0,0012 0,0006 0,0003 |
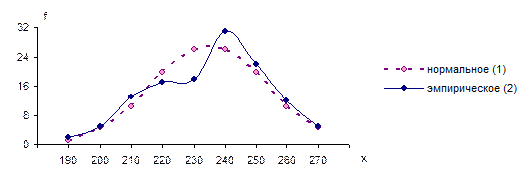
График на рис. 9.1 наглядно демонстрирует близость эмпирического (2) и нормального (1) распределений.
Рис. 9.1. Распределения филиалов почтовой связи по численности работников: 1 – нормальное; 2 – эмпирическое.
Для математического обоснования близости эмпирического распределения закону нормального распределения рассчитываются критерии согласия .
Критерий Колмогорова – критерий согласия, позволяющий оценить степень близости эмпирического распределения к нормальному. А. Н. Колмогоров предложил для определения соответствия между эмпирическим и теоретическим нормальным распределениями использовать максимальную разность накопленных частот или частостей этих рядов. Для проверки гипотезы о соответствии эмпирического распределения закону нормального распределения рассчитывают критерий согласия l = D/ 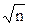
На основании значения Р(l) делают определенные выводы: если вероятность Р(l) достаточно велика, то гипотезу о соответствии фактического распределения нормальному закону можно считать подтвержденной; если вероятность Р(l) мала, то нулевая гипотеза отвергается, расхождения между фактическим и теоретическим распределениями признаются существенными.
Значения вероятностей для критерия согласия l:
| l | Р(l) | l | Р(l) | l | Р(l) |
| 0,3 | 1,000 | 0,8 | 0,544 | 1,5 | 0,022 |
| 0,4 | 0,997 | 0,9 | 0,399 | 1,8 | 0,013 |
| 0,5 | 0,964 | 1,0 | 0,27 | 2,0 | 0,006 |
| 0,6 | 0,864 | 1,1 | 0,18 | 2,1 | 0,003 |
| 0,7 | 0,711 | 1,2 | 0,11 | 2,3 | 0,000 |
Критерии Пирсона c 2 ("хи-квадрат") – критерий согласия, позволяющий оценить степень близости эмпирического распределения к нормальному:
Уровень значимости выбирается так, что Р(c 2 расч>c 2 табл) = a. Число степеней свободы равно h–l, где h – число групп; l – число условий, которые должны выполняться при вычислении теоретических частот. Для расчета теоретических частот кривой нормального распределения по формуле 

В этом случае нулевая гипотеза отвергается. Если c 2 расч£ c 2 табл, т.е. рассчитанный критерий не превышает максимально возможное расхождение частот, которое может возникнуть в силу случайности, то в данном случае гипотеза о соответствии распределений принимается. Критерий Пирсона эффективен при значительном числе наблюдений (n³50), причем частоты всех интервалов должны насчитывать не менее пяти единиц (при меньшем количестве интервалы объединяют), а число интервалов (групп) должно быть большим (h>5), поскольку оценка c 2 зависит от числа степеней свободы.
Критерий Романовского – критерий согласия, позволяющий оценить степень близости эмпирического распределения к нормальному. В.И. Романовский предложил близость эмпирического распределения к кривой нормального распределения оценивать по отношению:
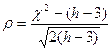
Если отношение больше 3, то расхождение частот эмпирического и нормального распределений нельзя признать случайным и гипотезу о нормальном законе распределения следует отвергнуть. Если отношение меньше или равно 3, то можно принять гипотезу о нормальном характере распределения данных.
Не нашли то, что искали? Воспользуйтесь поиском:
Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и исследование формы распределения, т.е. оценку симметричности и эксцесса.
Из математической статистики известно, что при увеличении объема статистической совокупности (N → 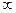
В статистике различают следующие виды кривых распределения:
Однородные совокупности описываются одновершинными распределениями. Многовершинность распределения свидетельствует о неоднородности изучаемой совокупности или о некачественном выполнении группировки.
Одновершинные кривые распределения делятся на симметричные, умеренно асимметричные и крайне асимметричные.
Распределение называется симметричным, если частоты любых 2-х вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. В таких распределениях x = Mo = Me .
Для характеристики асимметрии используют коэффициенты асимметрии.
Наиболее часто используются следующие из них:
• Коэффициент асимметрии Пирсона 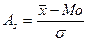
В одновершинных распределениях величина этого показателя изменяется от -1 до +1, в симметричных распределениях As=0.
При As>0 наблюдается правосторонняя асимметрия. В распределениях с правосторонней асимметрией Mo ≤ Me ≤ x .
Чем ближе по модулю As к 1, тем асимметрия существеннее:
– если |As| 0,5 – асимметрия значительна.
Коэффициент асимметрии Пирсона характеризует асимметрию только в центральной части распределения, поэтому более распространенным и более точным является коэффициент асимметрии, рассчитанный на основе центрального момента 3-его порядка:

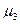
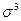
Центральным моментом в статистике называется среднее отклонение индивидуальных значений признака от его среднеарифметической величины.
Центральный момент k-ого порядка рассчитывается как:
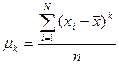
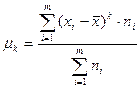
Соответственно формулы для определения центрального момента третьего порядка имеют следующий вид:
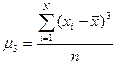
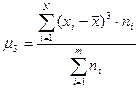
Для оценки существенности рассчитанного вторым способом коэффициента асимметрии определяется его средняя квадратическая ошибка:
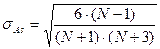
Если 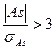
Для одновершинных распределений рассчитывается еще один показатель оценки его формы – эксцесс. Эксцессявляется показателем островершинности распределения. Он рассчитывается для симметричных распределений на основе центрального момента 4-ого порядка
где 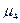
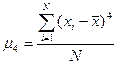

При симметричных распределениях Ех=0, если Ех>0, то распределение относится к островершинным, если Ех
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8829 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Читайте также:
- A) В примере сформировать прерывания вручную
- I Определение показателей опасности выбросов
- II) Вероятностные методы расчета надежности систем.
- II. Примеры слов, имеющих древнейшее германское происхождение
- III.9. Пример Ирландии
- IV.4. Пример Северной Норвегии
- SWOT – анализ на примере фабрики по производству обуви.
- А28. Выговор, увольнение с работы, штраф, лишение свободы являются примерами
- Абсолютные и средние показатели вариации
- Абсолютные показатели вариации
- Абсолютные показатели вариации
- Автоматизированного расчета электрических цепей
РАСЧЕТ ПОКАЗАТЕЛЕЙ ВАРИАЦИИ
ПРАКТИЧЕСКАЯ РАБОТА 3
Цель работы: получение практических навыков в расчете различных показателей (меры) вариации в зависимости от поставленных исследованием задач.
Порядок выполнения работы:
1. Определить вид и форму (простая или взвешенная) показателей вариации.
2. Рассчитать показатели степени вариации для сгруппированных и несгруппированных данных и показатели формы распределения.
3. Сформулировать выводы.
1. Определение вида и формы показателей вариации.
Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным относятся: размах вариации, квартильное отклонение, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Относительными показателями являются коэффициенты осцилляции, вариации, относительное линейное отклонение, относительный показатель квартильной вариации и т. д.
Размах вариации (R) является наиболее простым измерителем вариации признака и определяется по следующей формуле:
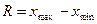
где 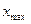
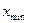
Квартильное отклонение (Q) – применяется для характеристики вариации признака в совокупности. Может использоваться вместо размаха вариации во избежание недостатков, связанных с использованием крайних значений.
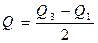
где 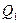
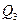
Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине 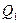
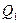
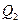
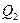
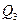
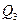
Квартили 1 и 3 определяются по формулам:
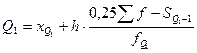

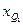
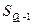
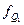
Причем 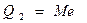
где Ме – медиана ряда;
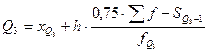
условные обозначения те же, что и для величин 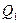
В симметричных или умеренно асимметричных распределениях Q»2/3s. Так как на квартильное отклонение не влияют отклонения всех значений признака, то его использование следует ограничить случаями, когда определение среднего квадратического отклонения затруднительно или невозможно.
Среднее линейное отклонение ( 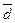
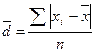
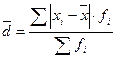
Дисперсия ( 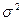
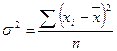
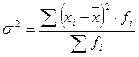
Среднее квадратическое отклонение (s) – наиболее распространенный показатель вариации, представляет собой квадратный корень из значения дисперсии.
Размах вариации, квартильное отклонение, среднее линейное и квадратическое отклонения – величины именованные, имеют размерность осредняемого признака. Дисперсия единицы измерения не имеет.
Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях вычисляются относительные показатели вариации. Базой для сравнения служит средняя арифметическая. Чаще всего относительные показатели выражаются в процентах и характеризуют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности.
Коэффициент осцилляции(относительный размах вариации) рассчитывается по формуле:
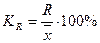
Линейный коэффициент вариации(относительное линейное отклонение):
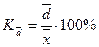
Относительный показатель квартильной вариации:
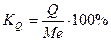
Коэффициент вариации:
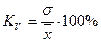
Наиболее часто применяемый в статистике показатель относительной колеблемости – коэффициент вариации. Его используют не только для сравнительной оценки вариации, но и как характеристику однородности совокупности. Чем больше величина коэффициента вариации, тем больше разброс значений признака вокруг средней, тем больше неоднородность совокупности. Существует шкала определения степени однородности совокупности в зависимости от значений коэффициента вариации (17; С.61).
Для получения приблизительного представления о форме распределения строят графики распределения (полигон и гистограмму).
В практике статистического исследования приходится встречаться с самыми различными распределениями. При изучении однородных совокупностей имеем дело, как правило, с одновершинными распределениями. Многовершинность свидетельствует о неоднородности изучаемой совокупности, появление двух и более вершин говорит о необходимости перегруппировки данных с целью выделения более однородных групп. Выяснение общего характера распределения предполагает оценку степени его однородности, а также вычисление показателей асимметрии и эксцесса. Симметричным является распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричных распределений средняя арифметическая, мода и медиана равны между собой. В связи с этим простейший показатель асимметрии основан на соотношении показателей центра распределения: чем больше разница между средними 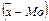
Для характеристики асимметричности в центральной части распределения, то есть основной массы единиц или для сравнительного анализа степени асимметрии нескольких распределений рассчитывают относительный показатель асимметрии К.Пирсона:
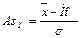
Величина показателя As может быть положительной и отрицательной. Положительная величина показателя указывает на наличие правосторонней асимметрии (правая ветвь относительно максимальной ординаты вытянута больше, чем левая). При правосторонней асимметрии между показателями центра распределения существует соотношение: 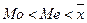
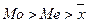
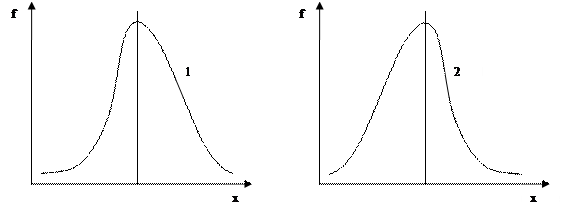 |
Рис. 1. Распределение:
1 – с левосторонней асимметрией; 2 – с правосторонней асимметрией.
Другой показатель, предложенный шведским математиком Линдбергом, рассчитывают по формуле:

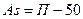
где П – процент тех значений признака, которые превосходят по величине среднюю арифметическую.
Наиболее точным и распространенным является показатель, основанный на определении центрального момента третьего порядка (в симметричном распределении его величина равна нулю):
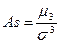
где 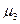
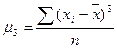
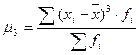
σ – среднеквадратическое отклонение.
Применение этого показателя дает возможность не только определить величину асимметрии, но и ответить на вопрос о наличии или отсутствии асимметрии в распределении признака в генеральной совокупности. Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, которая зависит от объема наблюдений n и рассчитывается по формуле:
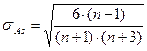
Если отношение 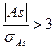
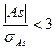

Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Линдбергом предложен следующий показатель для оценки эксцесса:
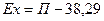
где П – доля (%) количества вариантов, лежащих в интервале, равном половине среднего квадратического отклонения в ту или другую сторону от средней арифметической.
Наиболее точным является показатель, использующий центральный момент четвертого порядка:
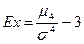
где 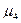
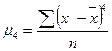
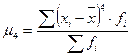
На рисунке 2 представлены два распределения: одно – островершинное (величина эксцесса положительная), второе – плосковершинное (величина эксцесса отрицательная). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. В нормальном распределении отношение 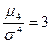
 |
Рис. 2. Распределение:
1,4 – нормальное; 2 – островершинное; 3 – плосковершинное
Средняя квадратическая ошибка эксцесса рассчитывается по формуле:
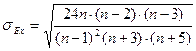
где n – число наблюдений.
Если 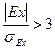
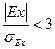
Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное эмпирическое исследование к типу кривых нормального распределения.
2. Рассмотрим методику исчисления показателей вариации.
Дата добавления: 2014-12-23 ; Просмотров: 5947 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет