Учитесь решать задачи по комбинаторике? На самом начальном этапе нужно изучить основные формулы комбинаторики: сочетания, размещения, перестановки (смотрите подробнее ниже) и научиться их применять для решения задач.
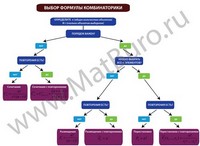
Как выбрать формулу комбинаторики?
Мы подготовили для вас наглядную схему с примерами решений по каждой формуле комбинаторики:
- алгоритм выбора формулы (сочетания, перестановки, размещения с повторениями и без),
- рекомендации по изучению комбинаторики,
- 6 задач с решениями и комментариями на каждую формулу.
Перестановки
Пусть имеется $n$ различных объектов.
Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.
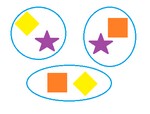
Пример всех перестановок из $n=3$ объектов (различных фигур) – на картинке справа. Согласно формуле, их должно быть ровно $P_3=3!=1cdot 2cdot 3 =6$, так и получается.
С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов – уже 3628800 (больше 3 миллионов!).
Размещения
Пусть имеется $n$ различных объектов.
Будем выбирать из них $m$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $m$, а их число равно
Пример всех размещений из $n=3$ объектов (различных фигур) по $m=2$ – на картинке справа. Согласно формуле, их должно быть ровно $A_3^2=3cdot (3-2+1)=3cdot 2 =6$.
Сочетания
Пусть имеется $n$ различных объектов.
Будем выбирать из них $m$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $m$, а их число равно
Пример всех сочетаний из $n=3$ объектов (различных фигур) по $m=2$ – на картинке справа. Согласно формуле, их должно быть ровно $C_3^2=frac<3!> <(3-2)!cdot 2!>=3$. Ясно, что сочетаний всегда меньше чем размещений (так как при размещениях порядок важен, а для сочетаний – нет), причем именно в $m!$ раз, то есть верна формула связи:
Объект исследования: формула комбинаторики для числа сочетаний с повторениями.
Результаты, полученные лично автором: рассмотрен способ построения форумы числа сочетаний с повторениями. Решены задачи, использующие данную формулу.
Сочетания с повторениями – это сочетание n объектов по k в предположении, что каждый объект может участвовать в сочетании несколько раз. Таким образом, сочетание с повторениями из n элементов по k элементов (при этом допускается, что m>n) может содержать любой элемент сколько угодно раз от 1 до k включительно или не содержать его совсем, т. е. каждое сочетание с повторениями из n элементов по k элементов может состоять не только из k различных элементов, но и k каких угодно и как угодно повторяющихся элементов.
Существует специальная формула для вычисления числа сочетаний с повторениями. Выведем эту формулу, используя пример. Пусть в кондитерском магазине продаются пирожные 4 видов: корзиночки, наполеоны, песочные и эклеры. Если куплено 3 корзиночки (к), 1 наполеон (н), 2 песочных (п) и 1 эклер (э), то получим такую запись:111|1|11|1.
В этой записи палочки отделяют одну группу пирожных от другой. Если же куплено 2 корзиночки и 5 песочных, то получим запись 11||11111|. Ясно, что разным покупкам соответствуют при этом разные комбинации из 7 единиц и 3 палочек. Обратно, каждой комбинации единиц и палочек соответствует какая-то покупка. Например, комбинации |111|1111| соответствует покупка 3 наполеонов и 4 песочных (крайние группы отсутствуют).
В результате мы получим столько единиц, сколько предметов входит в комбинацию, т. е. k, а число палочек будет на 1 меньше, чем число типов предметов, т. е. n–1. Таким образом, мы получим перестановки с повторениями из k единиц и n–1 палочек. Различным комбинациям при этом соответствуют различные перестановки с повторениями, а каждой перестановке с повторениями соответствует своя комбинация.
Итак, число 

Рассмотрим задачу. Сколько можно построить различных прямоугольных параллелепипедов, длина каждого ребра которых является целым числом от 1 до 10? Ответ:
Материал поступил в редколлегию 24.04.2017
УДК 519.253
Научный руководитель: доцент кафедры «Высшая математика»,
к.т.н. А.Г. Белоусов
Анализ качества результатов социологических
Опросов
Объект исследования: результаты социологических опросов.
Результаты, полученные лично автором: проанализированы данные реальных социологических исследований, на основе которых предложена методика выявления недостоверности результатов опросов, опирающаяся на методы теории вероятности и математической статистики.
Результаты социологических опросов, как правило, представляют собой не только информацию, но и средство влияния на принятие решений, также они могут влиять на общественное мнение. Поскольку проведение масштабных опросов требует значительных затрат, а в случае использования результатов опросов в ненаучных целях требуются данные, подтверждающие определённый тезис, в некоторых случаях публикуются фальшивые результаты опросов: действительные результаты – иные, либо опрос на самом деле не проводится.
Сфальсифицированные результаты опросов можно условно разделить на три уровня: 1) фальсификация выявляется с помощью комбинирования арифметики и методов теории вероятностей и математической статистики, 2) выявление фальсификации требует существенного опыта в сфере теории вероятностей и математической статистики, 3) соблюдение требований предыдущего уровня, а также сбор дополнительных эмпирических данных. При этом анализ, как правило, не предоставляет строгого доказательства, что результаты опроса недостоверные, но он может позволить выявить данные, являющиеся недостоверными с высокой вероятностью.
К признакам потенциально сфальсифицированных результатов опросов, по нашему мнению, относятся: общее кратное процентов голосов, круглые величины в процентах, погрешности при суммировании процентов. Рассмотрим более детально случаи «странных» результатов с использованием центральной предельной теоремы (ЦПТ) – для вопросов с выбором нескольких вариантов.
В анкетных листах нередко встречаются вопросы, где можно выбрать несколько вариантов ответа, всего не более k, при этом вариант вида «затрудняюсь ответить» не предусматривается. Любой респондент может выбрать число вариантов от 1 до k. Допустим, выбор варианта респондентом – случайная величина. Таким образом, количество процентов, набираемых всеми вариантами по всей выборке, – случайная величина, являющаяся суммой большого числа n одинаково распределённых независимых случайных величин (никакой респондент не знает, какие варианты выбирают другие респонденты), где n – размер выборки. Согласно ЦПТ распределение суммарного процента должно быть близко к нормальному. Следовательно, если суммарный процент оказался близок к 100 или 100k, это может быть вызвано наличием сфабрикованных данных, поскольку такое случайное событие маловероятно. Если в опросе есть ряд вопросов с k>1, и хотя бы 3-4 вопроса дают суммарный процент ответов, близкий к одной из границ, следует тщательно изучить данные опроса на предмет подтасовок или непреднамеренных ошибок.
Так, в нескольких найденных источниках приводятся случаи при k=3, когда суммарный процент составлял более 260, что требует дополнительных исследований на предмет причин таких показателей. Особенно важна проверка близости к верхней границе (300% для k=3). Естественно, постоянная близость суммы процентов к одному и тому же значению, включая «идеальное» 50(k+1), также должна являться аргументом для расследования.
Ещё одним примером возможного низкого качества результатов опроса может являться следующая ситуация. Так, в публикациях, касающихся опросов проводимых среди студентов вузов, насчитывающих 5-10 тыс. чел., часто фигурирует размер выборки порядка 100-200. Допустим, в некотором вузе есть 5 тыс. студентов, и по данным было опрошено 200 студентов, то есть 0,04=4% от контингента. Вероятность неучастия в опросе составит 0,96 для взятого наугад студента, для каждого последующего она медленно убывает, если все предыдущие ответили отрицательно. Если есть разнообразие по курсам и специальностям среди студентов (гарантированная случайность выборки), то для 50 человек вероятность отсутствия среди них участника опроса составит менее 13%. Уже для 60 студентов она составит менее 9%. При увеличении числа потенциальных «неучастников» с высокой долей вероятности можно утверждать, что: имел место несуществующий опрос, или репрезентативность выборки оказалась крайне низкая (например, посещено 2-3 поточных лекции, где и было отобрано 200 респондентов).
Преимущества математических методов анализа заключаются в том, что большинство из них достаточно быстры в применении и не требуют детальных данных об опросе. Кроме того, большинство из них могут быть использованы «здесь и сейчас», на основе компьютерных технологий и интернет-ресурсов.
Положительные результаты применения математических методов свидетельствуют о высокой вероятности некачественных данных, однако не гарантируют, что не имеет место случайности, или что результаты вызваны не преднамеренной подтасовкой, а ошибками при обеспечении репрезентативности данных и подсчётах результатов организаторами опроса. Вследствие этого целесообразно использовать математические методы как дополнение к нематематическим способам выявления подтасовок.
Материал поступил в редколлегию 27.04.2017
УДК 519.2
Научный руководитель: ассистент кафедры «Высшая математика»,
Рассмотрим следующие возможные способы выбора.
1. Выбор с возвращением: каждый вынутый шар возвращается в урну, каждый следующий шар выбирается из полной урны. В полученном наборе из номеров шаров могут встречаться одни и те же номера. 2. Выбор без возвращения: вынутые шары в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера.
Условимся, какие результаты выбора (наборы из номеров шаров) мы будем считать различными. Есть ровно две возможности.
1. Выбор с учётом порядка : два набора номеров шаров считаются различными, если они отличаются составом или порядком номеров. Так, при выборе трёх шаров из урны, содержащей 5 шаров, наборы (1, 5, 2), (2, 5, 1) и (4, 4, 5) различны, если порядок учитывается. 2. Выбор без учёта порядка : два набора номеров шаров считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми.
Так, наборы (1, 5, 2) и (2, 5, 1) не различаются и образуют один и тот же результат выбора, если порядок не учитывается.
Подсчитаем, сколько возможно различных результатов для каждой из четырёх схем выбора (выбор с возвращением или без, и в каждом из этих случаев с учётом порядка или без).
и называется числом размещений из элементов по элементов.
равно . Для каждой такой пары есть способа выбрать третий шар. По теореме 1, число возможных троек
равно произведению числа пар и числа способов выбора третьего шара, т.е. равно . Продолжая рассуждения, получим, что общее число возможных наборов из шаров равно . В этом произведении сомножителей последний множитель есть число способов выбора -го шара, когда уже выбраны предыдущие.
и называется числом сочетаний из элементов по элементов.
| с учётом порядка | без учёта порядка |
| (1,1) | (1,1) |
| (2,2) | (2,2) |
| (1,2) (2,1) |
> (1,2) |
Видим, что в схеме «без учёта порядка» получилось три различных результата, в отличие от четырёх результатов в схеме «с учётом порядка». Заметим также, что никаким делением на «число каких-нибудь перестановок», которое помогло избавиться от учёта порядка при выборе без возвращения, число 3 из числа 4 получить не удастся.
Представим себе другой эксперимент, имеющий точно такие же результаты, и посчитаем их количество. Есть ящиков, в которых размещаются шаров. Нас интересует только число шаров в каждом ящике. Результатом эксперимента снова является набор чисел , где равно числу шаров в ящике с номером , и . Числа принимают натуральные значения или равны нулю.
А теперь изобразим результат такого размещения в виде схемы, в которой вертикальные линии обозначают перегородки между ящиками, а точки находящиеся в ящиках шары:
Мы видим результат размещения девяти шаров по семи ящикам. Первый ящик содержит три шара, второй и шестой ящики пусты, третий ящик содержит один шар, в четвёртом и пятом ящиках лежит по два шара. Переложим один шар из первого ящика во второй и изобразим таким же образом ещё два результата размещения:
Видим, что все размещения можно получить, меняя между собой шары и перегородки, или расставляя шаров на местах. Число получается так: у ящиков есть ровно перегородка, считая крайние, но из них перемещать можно лишь внутреннюю перегородку. Таким образом, имеется мест, которые можно занять шарами либо внутренними перегородками. Перебрав все возможные способы расставить шаров на этих местах (заполняя оставшиеся места перегородками), переберем все нужные размещения.
Осталось заметить, что способов расставить шаров на местах существует
Именно столько есть способов выбрать из номеров мест номеров мест для шаров.