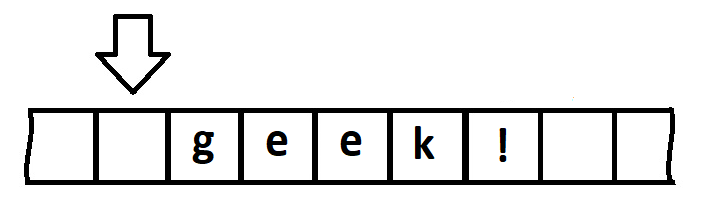Содержание
- 1 Содержание
- 2 Устройство [ править | править код ]
- 3 Описание машины Тьюринга [ править | править код ]
- 4 Пример [ править | править код ]
- 5 Полнота по Тьюрингу [ править | править код ]
- 6 Варианты машины Тьюринга [ править | править код ]
- 7 Что такое машина Тьюринга
- 8 Зачем это программисту
- 9 Полнота по Тьюрингу
- 10 Тест по Тьюрингу
- 11 Что такое машина Тьюринга
- 12 Зачем это программисту
- 13 Полнота по Тьюрингу
- 14 Тест по Тьюрингу
Маши́на Тью́ринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.
Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать всех исполнителей (с помощью задания правил перехода), каким-либо образом реализующих процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
То есть всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга [1] .
Содержание
Устройство [ править | править код ]
В состав машины Тьюринга входит неограниченная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки [2] [3] , и управляющее устройство (также называется головкой записи-чтения (ГЗЧ)), способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.
Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.
Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.
Описание машины Тьюринга [ править | править код ]
Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: qiaj→qi1aj1dk (если головка находится в состоянии qi, а в обозреваемой ячейке записана буква aj, то головка переходит в состояние qi1, в ячейку вместо aj записывается aj1, головка делает движение dk, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации имеется ровно одно правило (для недетерминированной машины Тьюринга может быть большее количество правил). Правил нет только для заключительного состояния, попав в которое, машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.
Пример [ править | править код ]
Пример машины Тьюринга для умножения чисел в унарной системе счисления. Запись правила «qiaj→qi1aj1R/L/N» следует понимать так: qi — состояние при котором выполняется это правило, aj — данные в ячейке, в которой находится головка, qi1 — состояние в которое нужно перейти, aj1 — что нужно записать в ячейку, R/L/N — команда на перемещение.
Машина работает по следующему набору правил:
| q | q1 | q2 | q3 | q4 | q5 | q6 | q7 | q8 |
|---|---|---|---|---|---|---|---|---|
| 1 | q1→q1R | q11→q2aR | q21→q21L | q31 → q4aR | q41→q41R | q71→q2aR | ||
| × | q×→q1×R | q2×→q3×L | q4×→q4×R | q6×→q7×R | q8×→q9×N | |||
| = | q2=→q2=L | q4=→q4=R | q7=→q8=L | |||||
| a | q2a→q2aL | q3a→q3aL | q4a→q4aR | q6a→q61R | q7a→q7aR | q8a→q81L | ||
| * | q*→q*R | q3*→q6*R | q4*→q51R | |||||
| q5 →q2*L |
| Начало | |
| q | начальное состояние. Ищем «x» справа. При нахождении переходим в состояние q1 |
|---|---|
| q1 | заменяем «1» на «а» и переходим в состояние q2 |
| Переносим все «1» из первого числа в результат | |
| q2 | ищем «х» слева. При нахождении переходим в состояние q3 |
| q3 | ищем «1» слева, заменяем её на «а» и переходим в состояние q4. |
В случае если «1» закончились, находим «*» и переходим в состояние q6
при нахождении «1» заменяем его на «а» и переходим в состояние q2
при нахождении «=» переходим в состояние q8
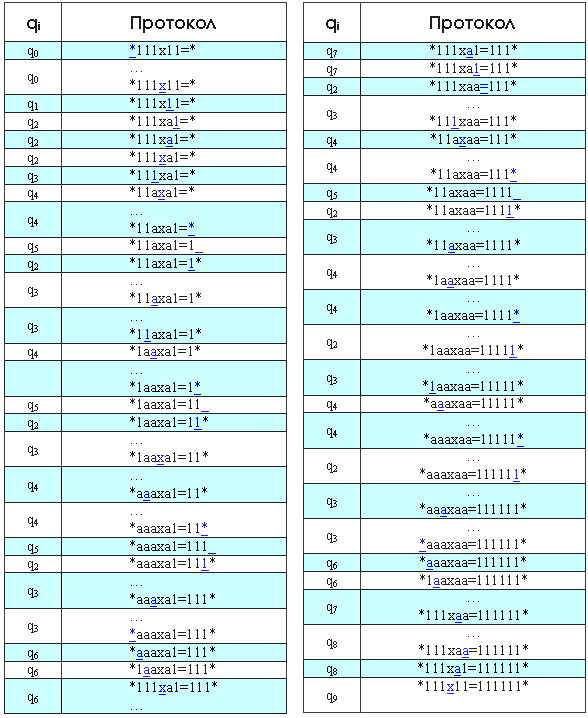
Умножим с помощью МТ 3 на 2 в единичной системе. В протоколе указаны начальное и конечное состояния МТ, начальная конфигурация на ленте и расположение головки машины (подчёркнутый символ).
Начало. Находимся в состоянии q, ввели в машину данные: *111×11=*, головка машины располагается на первом символе *.
1-й шаг. Смотрим по таблице правил что будет делать машина, находясь в состоянии q и над символом «*». Это правило из 1-го столбца 5-й строки — q*→q*R. Это значит, что мы переходим в состояние q (то есть не меняем его), символ станет «*» (то есть не изменится) и смещаемся по введённому нами тексту «*111×11=*» вправо на одну позицию (R), то есть на 1-й символ 1. В свою очередь, состояние q1 (1-й столбец 1-я строка) обрабатывается правилом q1→q1R. То есть снова происходит просто переход вправо на 1 позицию. Так происходит, пока мы не станем на символ «х». И так далее: берём состояние (индекс при q), берём символ, на котором стоим (подчёркнутый символ), соединяем их и смотрим обработку полученной комбинации по таблице правил.
Простыми словами, алгоритм умножения следующий: помечаем 1-ю единицу 2-го множителя, заменяя её на букву «а», и переносим весь 1-й множитель за знак равенства. Перенос производится путём поочерёдной замены единиц 1-го множителя на «а» и дописывания такого же количества единиц в конце строки (слева от крайнего правого «*»). Затем меняем все «а» до знака умножения «х» обратно на единицы. И цикл повторяется. Действительно, ведь A умножить на В можно представить как А+А+А В раз. Помечаем теперь 2-ю единицу 2-го множителя буквой «а» и снова переносим единицы. Когда до знака «=» не окажется единиц — значит умножение завершено.
Полнота по Тьюрингу [ править | править код ]
Можно сказать, что машина Тьюринга представляет собой простейшую вычислительную машину с линейной памятью, которая согласно формальным правилам преобразует входные данные с помощью последовательности элементарных действий.
Элементарность действий заключается в том, что действие меняет лишь небольшой фрагмент данных в памяти (в случае машины Тьюринга — лишь одну ячейку), и число возможных действий не бесконечно. Несмотря на простоту машины Тьюринга, на ней можно вычислить всё, что можно вычислить на любой другой машине, осуществляющей вычисления с помощью последовательности элементарных действий. Это свойство называется полнотой.
Один из естественных способов доказательства того, что алгоритмы вычисления, которые можно реализовать на одной машине, можно реализовать и на другой, — это имитация первой машины на второй.
Имитация заключается в следующем. На вход второй машине подаётся описание программы (правил работы) первой машины D <displaystyle D> 


Как было сказано, на машине Тьюринга можно имитировать (с помощью задания правил перехода) все другие исполнители, каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
На машине Тьюринга можно имитировать машину Поста, нормальные алгоритмы Маркова и любую программу для обычных компьютеров, преобразующую входные данные в выходные по какому-либо алгоритму. В свою очередь, на различных абстрактных исполнителях можно имитировать Машину Тьюринга. Исполнители, для которых это возможно, называются полными по Тьюрингу (Turing complete).
Есть программы для обычных компьютеров, имитирующие работу машины Тьюринга. Но следует отметить, что данная имитация неполная, так как в машине Тьюринга присутствует абстрактная бесконечная лента. Бесконечную ленту с данными невозможно в полной мере имитировать на компьютере с конечной памятью: суммарная память компьютера — оперативная память, жёсткие диски, различные внешние носители данных, регистры и кэш процессора и др. — может быть очень большой, но, тем не менее, всегда конечна. Теоретический предел количества информации, которая может находиться внутри заданной поверхности, с точностью до множителя 1 / ln 2 <displaystyle 1/ln <2>> 
Варианты машины Тьюринга [ править | править код ]
Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга.
Машина Тьюринга, работающая на полубесконечной ленте [ править | править код ]
В качестве примера такого сведения рассмотрим следующую теорему: Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте (то есть на ленте, бесконечной в одну сторону).
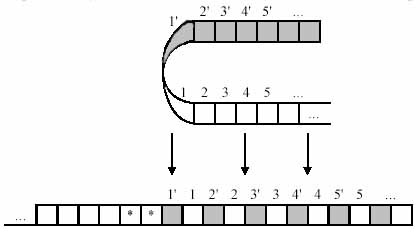
Рассмотрим доказательство, приведённое Ю. Г. Карповым в книге «Теория автоматов». Доказательство этой теоремы конструктивное, то есть мы дадим алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Во-первых, произвольно занумеруем ячейки рабочей ленты МТ, то есть определим новое расположение информации на ленте:
Затем перенумеруем ячейки, причём будем считать, что символ «*» не содержится в словаре МТ:
Наконец, изменим машину Тьюринга, удвоив число её состояний, и изменим сдвиг головки считывания-записи так, чтобы в одной группе состояний работа машины была бы эквивалентна её работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе МТ встретится символ ‘*’, значит головка считывания-записи достигла границы зоны:
Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации. Очевидно, что слева от ограничивающих маркеров «*» лента в эквивалентной машине Тьюринга не используется.
Что такое машина Тьюринга
Для того, чтобы представить простейшую машину Тьюринга, взглянем на её художественную реализацию:
Это бесконечная лента, не имеющая ни начала, ни конца, поделённая на ячейки. Для работы с ней мы используем некое управляющее устройство (автомат), для визуализации выбрана каретка. В каждый момент времени она имеет состояние qj и считывает содержимое ячейки ai. О том, что происходит в остальной части ленты, каретка не знает, соответственно оперировать она может только текущими данными. Всего возможно три типа действий, зависящий от этой композиции:
- выполнить сдвиг на соседнюю ячейку;
- записать в текущую новое содержимое;
- изменить состояния.
Что-то похожее реализовано в электронных таблицах: там тоже условно неограниченное поле, вы можете изменить значение ячейки, изменить действие или перейти на другую ячейку.
Множества A = и Q = являются конечными, a0 – символ пустой ячейки, q1 – начальное состояние, q0 – пассивное состояния, условие выхода машины из цикла.
Создадим таблицу для реализации алгоритма Тьюринга:
Символами _Л, _П, _Н обозначим направление движения автомата – соответственно сдвиг «влево», «вправо» или неподвижное положение.
Пусть наша лента выглядит так:
Начальное положение – крайняя правая ячейка, остановка – в пустой клетке. Догадались как она будет выглядеть после завершения алгоритма?
На указанном примере всё выглядит довольно просто. Можете поиграть с увеличением алфавита, преобразованием состояний, помещением начальной позиции не в крайнюю позиции, условиями выхода из цикла и т.д. Фактически, практически любую задачу преобразования можно решить с помощью машины Тьюринга.
Зачем это программисту
Машина Тьюринга позволяет размять мозги и взглянуть на решение задачи иначе. В конечном счёте, с той же целью следует познакомиться с:
- нормальным алгоритмом Маркова;
- лямбда-вычислениями;
- языком программирования Brainfuck.
Но машина Тьюринга – базовая теория алгоритмов, которая помогает думать не столько о средствах языка, сколько о различных путях решения задачи. Для профессионального роста – это необходимый навык.
Полнота по Тьюрингу
Ещё один важный вопрос, связанный с именем известного математика. На форумах и в статьях вы неоднократно могли видеть выражение «полныйне полный язык программирования по Тьюрингу». Ответ на вопрос «что это означает?» возвращает нас к описанной выше теории. Как уже было сказано, машина Тьюринга позволяет выполнить любое преобразование, соответственно, вы можете реализовать на ней абсолютно любой алгоритм или функцию. То же самое относится и к языкам. Если с его помощью вы можете реализовать любой заданный алгоритм – он тьюринг-полный. Если в дело вступают ограничения синтаксиса или любые физические – не полный.
Тест по Тьюрингу
Последний раздел никак не связан с машиной. Тест Тьюринга – игра, в ходе которой человек с помощью текстовых сообщений взаимодействует одновременно с машиной и другим человеком, не видя их. Задача машины – ввести участника в заблуждение.
Такой тест на долгие годы предопределил развитие ИИ – программы вроде Элизы или PARRY строились именно на копировании человеческого поведения машиной. Уже позднее, когда стало понятно, что путь тупиковый, вектор развития был сдвинут в сторону изучения механизмов интеллекта. Однако до сих пор тема «способна ли мыслить машина» лежит в основе многих тестов, романов и кинофильмов.
Алан Тьюринг остался в истории не только человеком, совершившим важное открытие во время Второй мировой войны, но и подаривший миру несколько фундаментальных теорий, которыми пользуется человечество до сих пор.
Если вы не учились профессии программиста в вузе или не ходили в специальную школу, то, возможно «Машина Тьюринга» для вас просто дешифратор из курса истории или фильма «Игра в имитацию». В действительности всё немного сложнее, любому уважающему себя программисту необходимо знать и понимать, что это такое.
Что такое машина Тьюринга
Для того, чтобы представить простейшую машину Тьюринга, взглянем на её художественную реализацию:
Это бесконечная лента, не имеющая ни начала, ни конца, поделённая на ячейки. Для работы с ней мы используем некое управляющее устройство (автомат), для визуализации выбрана каретка. В каждый момент времени она имеет состояние qj и считывает содержимое ячейки ai. О том, что происходит в остальной части ленты, каретка не знает, соответственно оперировать она может только текущими данными. Всего возможно три типа действий, зависящий от этой композиции:
- выполнить сдвиг на соседнюю ячейку;
- записать в текущую новое содержимое;
- изменить состояния.
Что-то похожее реализовано в электронных таблицах: там тоже условно неограниченное поле, вы можете изменить значение ячейки, изменить действие или перейти на другую ячейку.
Множества A = и Q = являются конечными, a0 – символ пустой ячейки, q1 – начальное состояние, q0 – пассивное состояния, условие выхода машины из цикла.
Создадим таблицу для реализации алгоритма Тьюринга:
Символами _Л, _П, _Н обозначим направление движения автомата – соответственно сдвиг «влево», «вправо» или неподвижное положение.
Пусть наша лента выглядит так:
Начальное положение – крайняя правая ячейка, остановка – в пустой клетке. Догадались как она будет выглядеть после завершения алгоритма?
На указанном примере всё выглядит довольно просто. Можете поиграть с увеличением алфавита, преобразованием состояний, помещением начальной позиции не в крайнюю позиции, условиями выхода из цикла и т.д. Фактически, практически любую задачу преобразования можно решить с помощью машины Тьюринга.
Зачем это программисту
Машина Тьюринга позволяет размять мозги и взглянуть на решение задачи иначе. В конечном счёте, с той же целью следует познакомиться с:
- нормальным алгоритмом Маркова;
- лямбда-вычислениями;
- языком программирования Brainfuck.
Но машина Тьюринга – базовая теория алгоритмов, которая помогает думать не столько о средствах языка, сколько о различных путях решения задачи. Для профессионального роста – это необходимый навык.
Полнота по Тьюрингу
Ещё один важный вопрос, связанный с именем известного математика. На форумах и в статьях вы неоднократно могли видеть выражение «полныйне полный язык программирования по Тьюрингу». Ответ на вопрос «что это означает?» возвращает нас к описанной выше теории. Как уже было сказано, машина Тьюринга позволяет выполнить любое преобразование, соответственно, вы можете реализовать на ней абсолютно любой алгоритм или функцию. То же самое относится и к языкам. Если с его помощью вы можете реализовать любой заданный алгоритм – он тьюринг-полный. Если в дело вступают ограничения синтаксиса или любые физические – не полный.
Тест по Тьюрингу
Последний раздел никак не связан с машиной. Тест Тьюринга – игра, в ходе которой человек с помощью текстовых сообщений взаимодействует одновременно с машиной и другим человеком, не видя их. Задача машины – ввести участника в заблуждение.
Такой тест на долгие годы предопределил развитие ИИ – программы вроде Элизы или PARRY строились именно на копировании человеческого поведения машиной. Уже позднее, когда стало понятно, что путь тупиковый, вектор развития был сдвинут в сторону изучения механизмов интеллекта. Однако до сих пор тема «способна ли мыслить машина» лежит в основе многих тестов, романов и кинофильмов.
Алан Тьюринг остался в истории не только человеком, совершившим важное открытие во время Второй мировой войны, но и подаривший миру несколько фундаментальных теорий, которыми пользуется человечество до сих пор.
Статья в разработке
В науке не обязательно решить задачу, иногда именно постановка задачи является самым главным, так как это определяет направление развития на многие годы, в то время как результат, обладая законченной ценностью, уже не несет в себе возможности к развитию. Существует небезосновательное мнение о том, что человек способен привыкнуть и приспособиться к любым условиям жизни. Если физические условия меняются на протяжении одной жизни незначительно, то информационная среда, а следовательно, и правила игры и свойственные им "выигрышные стратегии" гораздо более изменчивы. Те из них, которые были признаны общественным мнением безусловно правильными в период детства и воспитания конкретного человека, всего лишь через несколько десятилетий могут оказаться совершенно бесперспективными, что находится в явном противоречии с необходимостью выживания. Или выживание не является такой уж необходимостью? Ответ на этот вопрос многое бы прояснил в решении конкретных жизненных ситуаций и особенно классической проблемы "отцов и детей", но, боюсь, единого мнения здесь сформировать не удастся. Каждый принимает решение о степени своей возможной адаптации сам. И каждый прав, но только для себя, какое бы он решение ни принял. Скорее всего, речь идет о неизбежной реализации предопределенной схемы поведения, заложенной генетически и функционирующей в соответствии с биологическим отсчетом времени на протяжении развития индивидуума, либо о "жестком ядре" личности и изменчивой, адаптирующейся внешней оболочке, причем граница между первым и вторым опять-таки определена генетическими особенностями на "аппаратном" уровне.
Но для Тьюринга, самостоятельно изучавшего квантовую физику и теорию относительности еще в школе, этот вопрос был решен однозначно. Он спроецировал на машину свое собственное отношение к миру, а принципы обработки информации, заложенные в нее, несомненно являются результатом интроспекции. Машина Тьюринга – это, прежде всего, модель самого Тьюринга, своеобразный "памятник нерукотворный" собственному интеллекту. Иными словами – особенности мировосприятия Тьюринга наиболее точным образом представляются его машиной.
Машина Тьюринга
Машина Тьюринга – модель вычислительного процесса, в которой каждый алгоритм разбивается на последовательность простых, элементарных шагов и представляет собой логическую конструкцию. Физически она состоит из ленты бесконечной длины, разделенной на ячейки, и головки, которая перемещается вдоль ленты и способна читать и записывать символы.
Была предложена в 1936 г. Аланом Тьюрингом для уточнения понятия алгоритма. Машина Тьюринга – прообраз программируемого компьютера, абстрактный универсальный исполнитель. Его абстрактность заключается в том, что он представляет собой логическую вычислительную конструкцию, а не реальную вычислительную машину. Термин «универсальный исполнитель» говорит о том, что данный исполнитель может имитировать любой другой исполнитель.
Машина Тьюринга была пригодна для решения любой разрешимой математической или логической задачи. Она предназначалась для выполнения логических операций: она могла читать, писать и стирать символы, записанные в клетках бесконечной ленты. Для выполнения всех этих действий предусмотрена специальная таблица правил, в которой прописано, что нужно делать при различных комбинациях текущих состояний и символов, прочитанных с ленты.
Почему надо «знать» машину Тюринга?
Потому, что Тюринг показал, что существуют задачи, которые алгоритмически неразрешимы. Первоначально это вызвало шок и непринятия такого «скверного» определения понятия алгоритм. Были предприняты многочисленные, но безуспешные попытки его «улучшить». Однако еще до Тюринга Геделем была сформулирована теорема о неполноте формальных исчислений.
Тюринг показал на примерах, что существуют задачи, для которых применение формальных методов требует бесконечно много времени для решения, т.е. решения практически нет. В то время как человек решает эти задачи очень просто. Это имеет важное практическое значение для разработчиков систем искусственного интеллекта. Так как определение алгоритма по Тюрингу (или Маркову) говорит, фактически, о невозможности создания систем искусственного интеллекта, которые были бы способны заменить человека. По крайней мере, пока не возникнет новая математика или не появятся биороботы, в которых мозг человека или другого существа будет объединен с возможностями большой вычислительной машины. (а работы в этом направлении уже ведутся).
Почему надо «знать» машину Тюринга? Потому, что это – Начала математики, в нем вводится понятие алгоритм. Тезис Тюринга: всякий алгоритм может быть реализован соответствующей машиной. Этот тезис является формальным определением алгоритма. Он позволяет доказывать существование или несуществование алгоритмов, описывая соответствующие машины Тюринга или доказывая невозможность их построения.
Не знать машину Тюринга – значит не знать математики.
Потому, что это – Начала программирования, в нем вводятся понятия алгоритм. К сожалению, у многих программистов тюринговское определение алгоритма заменяется на своё, более близкое: алгоритм – эта программа, которую пишу Я.
Но если вы не знаете, что такое алгоритм, то как вы можете говорить, что вы запрограммировали алгоритм решения какой-либо задачи.
Потому, что машины Тюринга были использованы в 40-ых годах прошлого века при разработке первых электронных вычислительных машин.
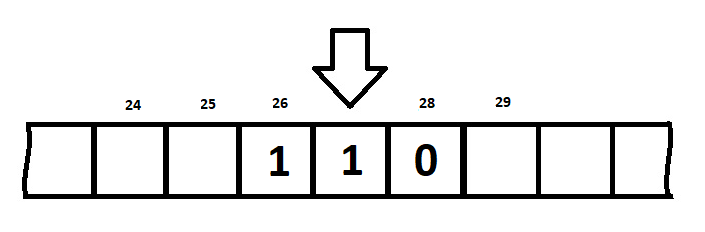
Потому, что, складывая в столбик, чтобы подсчитать свои суммарные денежные затраты, например, мы фактически реализуем машину Тюринга. Действительно, как выполняется сложение в столбик:
7 + 4 – мы ведь реально не производим вычисления, не прибавляем как школьники первого класса к 7 палочкам еще 4 палочки. Нет, мы знаем что 7+4 = 1 и 1 «в памяти».
Т.е. ее надо перенести влево как это и делается в машине Тюринга. Точно также мы складывая 8 и 0 получаем 8, но так как мы находимся в особом состоянии, которое называется «перенос единицы» мы знаем, что в нижней строке надо записать 9.
Вместо реальных вычислений производится формальная замена одних символов другими. Но интерпретировать записанную последовательность символов «791» как число или как текст или другим образом зависит целиком от нас.
Семантическая интерпретация последовательности символов целиком зависит от контекста, от наших соглашений с другими людьми. Например, FF можно интерпретировать как пару букв латинского алфавита, а можно как число 255, записанное в шестнадцатиричной системе. Так что считать ли FF частью номера автомобиля или числом зависит только от нас.
Еще один пример. Вспомним, что А.Марков дал другое определение алгоритма. Со школьной скамьи мы знаем, что 7х8 = 56. Если кто забыл об этом, то можно освежить свою память, посмотрев на обложку школьной тетради. Здесь имеет место употребления нормальных алгоритмов Маркова. Цепочка символов 7х8 заменяется на цепочку 56. Никаких действий не происходит.