Задачи с игральными костями теория вероятности

Еще одна популярная задача теории вероятностей (наравне с задачей о подбрасывании монет) – задача о подбрасывании игральных костей.

Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.

Основной метод решения подобных задач – использование формулы классической вероятности, который мы и разберем на примерах ниже.

Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).

Одна игральная кость

С одной игральной костью дело обстоит до неприличия просто. Напомню, что вероятность находится по формуле $P=m/n$, где $n$ – число всех равновозможных элементарных исходов эксперимента с подбрасыванием кубика или кости, а $m$ – число тех исходов, которые благоприятствуют событию.

Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?

Так как игральная кость представляет собой кубик (еще говорят, правильная игральная кость, то есть кубик сбалансированный, так что выпадает на все грани с одинаковой вероятностью), граней у кубика 6 (с числом очков от 1 до 6, обычно обозначаемых точкам), то и общее число исходов в задаче $n=6$. Благоприятствуют событию только такие исходы, когда выпадет грань с 2, 4 или 6 очками (только четные), таких граней $m=3$. Тогда искомая вероятность равна $P=3/6=1/2=0.5$.

Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.

Рассуждаем также, как и в предыдущем примере. Общее число равновозможных исходов при бросании игрального кубика $n=6$, а условию "выпало не менее 5 очков", то есть "выпало или 5, или 6 очков" удовлетворяют 2 исхода, $m=2$. Нужная вероятность равна $P=2/6=1/3=0.333$.

Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.

Две игральные кости

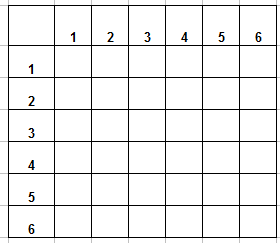
Когда речь идет о задачах с бросанием 2 костей, очень удобно использовать таблицу выпадения очков. По горизонтали отложим число очков, которое выпало на первой кости, по вертикали – число очков, выпавшее на второй кости. Получим такую заготовку (обычно я делаю ее в Excel, файл вы сможете скачать ниже):

А что же в ячейках таблицы, спросите вы? А это зависит от того, какую задачу мы будем решать. Будет задача про сумму очков – запишем туда сумму, про разность – запишем разность и так далее. Приступаем?

Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.

Сначала разберемся с общим числом исходов эксперимента. когда мы бросали одну кость, все было очевидно, 6 граней – 6 исходов. Здесь костей уже две, поэтому исходы можно представлять как упорядоченные пары чисел вида $(x,y)$, где $x$ – сколько очков выпало на первой кости (от 1 до 6), $y$ – сколько очков выпало на второй кости (от 1 до 6). Очевидно, что всего таких пар чисел будет $n=6cdot 6=36$ (и им соответствуют как раз 36 ячеек в таблице исходов).

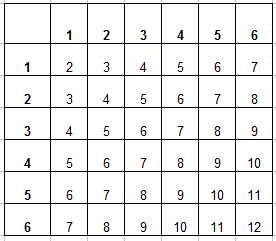
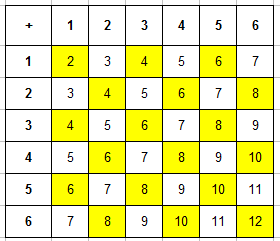
Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:

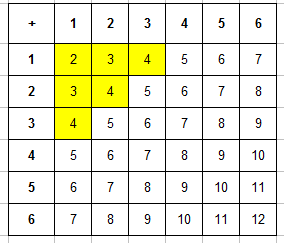
Теперь эта таблица поможем нам найти число благоприятствующих событию "в сумме выпадет менее 5 очков" исходов. Для этого подсчитаем число ячеек, в которых значение суммы будет меньше 5 (то есть 2, 3 или 4). Для наглядности закрасим эти ячейки, их будет $m=6$:

Тогда вероятность равна: $P=6/36=1/6$.

Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.

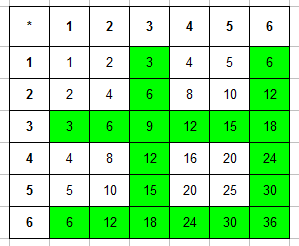
Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:

Остается только записать, что общее число исходов $n=36$ (см. предыдущий пример, рассуждения такие же), а число благоприятствующих исходов (число закрашенных ячеек в таблице выше) $m=20$. Тогда вероятность события будет равной $P=20/36=5/9$.

Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).

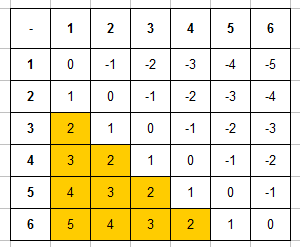
Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.

Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:

Итак, что общее число равновозможных элементарных исходов $n=36$, а число благоприятствующих исходов (число закрашенных ячеек в таблице выше) $m=10$. Тогда вероятность события будет равной $P=10/36=5/18$.

Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).

Другие задачи про кости и кубики

Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.

Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.

В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.

Найдем общее число исходов эксперимента. Исходы можно представлять как упорядоченные тройки чисел вида $(x,y,z)$, где $x$ – сколько очков выпало на первой кости (от 1 до 6), $y$ – сколько очков выпало на второй кости (от 1 до 6), $z$ – сколько очков выпало на третьей кости (от 1 до 6). Очевидно, что всего таких троек чисел будет $n=6cdot 6cdot 6=216$ .

Теперь подберем такие исходы, которые дают в сумме 15 очков.

Получили $m=3+6+1=10$ исходов. Искомая вероятность $P=10/216=0.046$.

Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.

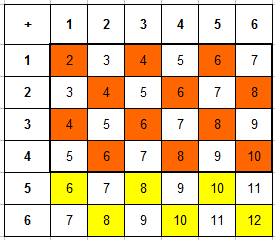
Наиболее простой способ решения этой задачи – снова воспользоваться таблицей (все будет наглядно), как и ранее. Выписываем таблицу сумм очков и выделяем только ячейки с четными значениями:

Получаем, что согласно условию эксперимента, всего есть не 36, а $n=18$ исходов (когда сумма очков четная).

Теперь из этих ячееек выберем только те, которые соответствуют событию "на первой кости выпало не более 4 очков" – то есть фактически ячейки в первых 4 строках таблицы (выделены оранжевым), их будет $m=12$.

Искомая вероятность $P=12/18=2/3.$

Эту же задачу можно решить по-другому, используя формулу условной вероятности. Введем события:
А = Сумма числа очков четная
В = На первой кости выпало не более 4 очков
АВ = Сумма числа очков четная и на первой кости выпало не более 4 очков
Тогда формула для искомой вероятности имеет вид: $$ P(B|A)=frac. $$ Находим вероятности. Общее число исходов $n=36$, для события А число благоприятствующих исходов (см. таблицы выше) $m(A)=18$, а для события АВ – $m(AB)=12$. Получаем: $$ P(A)=frac=frac<18><36>=frac<1><2>; quad P(AB)=frac=frac<12><36>=frac<1><3>;\ P(B|A)=frac=frac<1/3><1/2>=frac<2><3>. $$ Ответы совпали.

Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.

В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.

Итак, имеем $n=4$ независимых испытания (броски кубика), вероятность выпадения четного числа очков в одном испытании (при одном броске кубика) равна $p=3/6=1/2=0.5$ (см. выше задачи для одной игральной кости).

Тогда по формуле Бернулли $P=P_n(k)=C_n^k cdot p^k cdot (1-p)^$, подставляя $k=3$, найдем вероятность того, что четное число очков появится 3 раза: $$ P_4(3)=C_4^3 cdot left(1/2
ight)^3 cdot left(1-1/2
ight)^1=4 cdot left(1/2
ight)^4=1/4=0,25. $$

Приведем еще пример, решаемый аналогичным образом.

Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.

Подставляем в формулу Бернулли следующие значения: $n=8$ (число бросков), $p=1/6$ (вероятность появления 6 при одном броске), $kge 1$ (хотя бы один раз появится шестерка). Прежде чем вычислять эту вероятность, напомню, что практически все задачи с формулировкой "хотя бы один. " удобно решать, переходя к противоположному событию "ни одного. ". В нашем примере сначала стоит найти вероятность события "Шестёрка не появится ни разу", то есть $k=0$: $$ P_8(0)=C_8^0 cdot left(1/6
ight)^0 cdot left(1-1/6
ight)^8=left(5/6
ight)^8. $$ Тогда искомая вероятность будет равна $$ P_8(kge 1)=1-P_8(0)=1-left(5/6
ight)^8=0.767. $$

Полезные ссылки

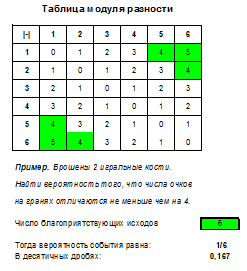
Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.

В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.

Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.

Еще по теории вероятностей:

В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):

Задача 1. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало очков, не меньшее, чем 3?

Число благоприятных исходов равно 4, т.е. выпадение граней кубика с числами 3, 4, 5 и 6. Всего равновозможных исходов 6. Таким образом, искомая вероятность равна

.

Ответ: .

Задача 2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков.

Благоприятных исходов 6:

Всего равновозможных исходов . Искомая вероятность равна

.

Ответ: .

Задача 3. Марина и Дина бросают кубик по одному разу. Выигрывает та девочка, у которой выпадет больше очков. Первой кубик бросила Марина, у нее выпало 3 очка. Найдите вероятность того, что Дина выиграет.

Кубик бросается один раз. Марина уже бросила кубик и у нее выпало 3 очка. Дина может выиграть у Марины, если при бросании игрального кубика выпадут числа 4, 5 или 6. Всего возможных исходов 6. Следовательно, вероятность того, что Дина выиграет, равна

.

Задача 4. Двое играют в кости – они по разу бросают игральный кубик. Выигрывает тот, у кого больше очков. Если выпадает поровну, то наступает ничья. Первый бросил кубик, и у него выпало 4 очка. Найдите вероятность того, что он выиграет.

Первый игрок может выиграть у второго игрока, если при бросании у второго игрока выпадут числа 1, 2 или 3, т.е. три благоприятных исхода. Всего исходов 6. Таким образом, искомая вероятность равна

.

Задача 5. Одновременно бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.

Так как бросается три игральных кости, то общее число исходов равно . Событию «в сумме выпало 5» благоприятствуют исходы:

Число таких исходов равно 6. Следовательно, искомая вероятность равна

.

Разделы: Математика

Тип урока: урок изучения нового материала.

Учащиеся должны знать:

• определение вероятности случайного события;
• уметь решать задачи на нахождение вероятности случайного события;
• уметь применять теоретические знания на практике.

Образовательные: создать условия для овладения учащимися системы знаний, умений и навыков с понятиями вероятности события.

Воспитательные: формировать у учащихся научное мировоззрение

Развивающие: развивать у учащихся познавательный интерес, творческие способности, волю, память, речь, внимание, воображение, восприятие.

Методы организации учебно-познавательной деятельности:

• наглядные,
• практические,
• по мыслительной деятельности: индуктивный,
• по усвоению материала: частично-поисковый, репродуктивный,
• по степени самостоятельности: самостоятельная работа,
• стимулирующие: поощрения,
• виды контроля: проверка самостоятельно решенных задач.

План урока

Устные упражнения

Изучение нового материала

Решение заданий.

Самостоятельная работа.

Подведение итогов урока.

Комментирование домашнего задания.

Оборудование: мультимедийный проектор (презентация), карточки (самостоятельная работа)

Ход урока

I. Организационный момент.

Организация класса в течение всего урока, готовность учащихся к уроку, порядок и дисциплина.

Постановка целей учения перед учащимися, как на весь урок, так и на отдельные его этапы.

Определить значимость изучаемого материала, как в данной теме, так и во все курсе.

II. Повторение

1. Что такое вероятность?

Вероятность – возможность исполнения, осуществимости чего-нибудь.

2. Какое определение дает основатель современной теории вероятностей А.Н. Колмогоров?

Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях.

3. Какое классическое определение вероятности дают авторы школьных учебников?

Вероятностью Р(А) события А в испытании с равновозможными элементарными исходами называется отношение числа исходов m, благоприятствующих событию А, к числу n всех исходов испытания.

Вывод: в математике вероятность измеряется числом.

Сегодня мы с вами продолжим рассматривать математическую модель “игральная кость”.

Предметом исследования в теории вероятностей являются события, появляющиеся при определенных условиях, которые можно воспроизводить неограниченное количество раз. Каждое осуществление этих условий называют испытанием.

Испытание – бросание игральной кости.

Событие – выпадение шестерки или выпадение четного числа очков.

Выпадение каждой грани при многократном бросании кубика имеет одинаковую вероятность (игральная кость правильная).

III. Устное решение задач.

1. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало 4 очка?

Решение. Случайный эксперимент – бросание кубика. Событие – число на выпавшей грани. Граней всего шесть. Перечислим все события: 1, 2, 3, 4, 5, 6. Значит п = 6. Событию А = <выпало 4 очка>благоприятствует одно событие: 4. Поэтому т = 1. События равновозможные, поскольку подразумевается, что кубик честный. Поэтому Р(А) = т/п = 1/6 = 0,17.

2. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало не более 4 очков?

Решение. Случайный эксперимент – бросание кубика. Событие – число на выпавшей грани. Значит п = 6. Событию А = <выпало не более 4 очков>благоприятствует 4 события: 1, 2, 3, 4. Поэтому т = 4. Поэтому Р(А) = т/п = 4/6 = 0,67.

3. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало менее 4 очков?

Решение. Случайный эксперимент – бросание кубика. Событие – число на выпавшей грани. Значит п = 6. Событию А = <выпало менее 4 очков>благоприятствует 3 события: 1, 2, 3. Поэтому т = 3. Р(А) = т/п = 3/6 = 0,5.

4. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало нечетное число очков?

Решение. Случайный эксперимент – бросание кубика. Событие – число на выпавшей грани. Значит п = 6. Событию А = <выпало нечетное число очков>благоприятствует 3 события: 1,3,5. Поэтому т = 3. Р(А) = т/п = 3/6 = 0,5.

IV. Изучение нового

Сегодня рассмотрим задачи, когда в случайном эксперименте используются две игральные кости или выполняются два, три броска.

1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 6. Ответ округлите до сотых.

Решение. Исход в этом опыте – упорядоченная пара чисел. Первое число выпадет на первом кубике, второе – на втором. Множество исходов удобно представить таблицей.

Строки соответствуют количеству очков на первом кубике, столбцы – на втором кубике. Всего элементарных событий п = 36.

1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

Напишем в каждой клетке сумму выпавших очков и закрасим клетки, где сумма равна 6.

Таких ячеек 5. Значит, событию А = <сумма выпавших очков равна 6>благоприятствует 5 исходов. Следовательно, т = 5. Поэтому, Р(А) = 5/36 = 0,14.

2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 3 очка. Результат округлите до сотых.

Решение. Исход в этом опыте – упорядоченная пара чисел. Всего событий п = 36.

Событию А = <сумма равна 3>благоприятствуют 2 исходов. Следовательно, т = 2.

Поэтому, Р(А) = 2/36 = 0,06.

3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет более 10 очков. Результат округлите до сотых.

Решение. Исход в этом опыте – упорядоченная пара чисел. Всего событий п = 36.

Событию А = <в сумме выпадет более 10 очков>благоприятствуют 3 исхода.

Следовательно, т = 3. Поэтому, Р (А) = 3/36 = 0,08.

4. Люба дважды бросает игральный кубик. В сумме у неё выпало 9 очков. Найдите вероятность того, что при одном из бросков выпало 5 очков.

Решение Исход в этом опыте – упорядоченная пара чисел. Первое число выпадет при первом броске, второе – при втором. Множество исходов удобно представить таблицей.

Строки соответствуют результату первого броска, столбцы – результату второго броска.

Всего событий, при которых сумма очков 9 будет п = 4. Событию А = <при одном из бросков выпало 5 очков>благоприятствует 2 исхода. Следовательно, т = 2.

Поэтому, Р(А) = 2/4 = 0,5.

5. Света дважды бросает игральный кубик. В сумме у неё выпало 6 очков. Найдите вероятность того, что при одном из бросков выпало 1 очко.

Первое бросание

Второе бросание

Сумма очков

Равновозможных исходов – 5.

Благоприятствующих исходов – 2.

Вероятность события р = 2/5 = 0,4.

6. Оля дважды бросает игральный кубик. В сумме у нее выпало 5 очков. Найдите вероятность того, что при первом броске выпало 3 очка.

Первое бросание

Второе бросание

Сумма очков

Равновозможных исходов – 4.

Благоприятствующих исходов – 1.

Вероятность события р = 1/4 = 0,25.

7. Наташа и Витя играют в кости. Они бросают игральную кость по одному разу.

Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 8 очков. Найдите вероятность того, что Наташа выиграла.

Наташа

Сумма очков

Равновозможных исходов – 5.

Благоприятствующих исходов – 2.

Вероятность события р = 2/5 = 0,4.

8. Таня и Наташа играют в кости. Они бросают игральную кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 6 очков. Найдите вероятность того, что Таня проиграла.

Равновозможных исходов – 5.

Благоприятствующих исходов – 2.

Вероятность события р = 2/5 = 0,4.

9. Коля и Лена играют в кости. Они бросают игральную кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. Первым бросил Коля, у него выпало 3 очка. Найдите вероятность того, что Лена не выиграет.

У Коли выпало 3 очка.

У Лены равновозможных исходов – 6.

Благоприятствующих проигрышу исходов – 3 (при1 и при 2 и при 3).

Вероятность события р = 3/6 = 0,5.

10. Маша трижды бросает игральный кубик. Какова вероятность того, что все три раза выпадут чётные числа.

У Маши равновозможных исходов – 6 · 6 · 6 = 216.

Благоприятствующих проигрышу исходов – 3 · 3 · 3 = 27.

Вероятность события р = 27/216 = 1/8 = 0,125.

11. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых.

Первая

Равновозможных исходов – 6 · 6 · 6 = 216.

Благоприятствующих исходов – 6.

Вероятность события р = 6/216 = 1/36 = 0,277… = 0,28. Следовательно, т = 3. Поэтому, Р (А) = 3/36 = 0,08.

V. Самостоятельная работа.

Вариант 1.

1. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало не менее 4 очков? (Ответ:0,5)
2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых. (Ответ:0,11)
3. Аня дважды бросает игральный кубик. В сумме у нее выпало 3 очка. Найдите вероятность того, что при первом броске выпало 1 очко. (Ответ:0,5)
4. Катя и Ира играют в кости. Они бросают игральную кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 9 очков. Найдите вероятность того, что Ира проиграла. (Ответ:0,5)
5. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 15 очков. Результат округлите до сотых. (Ответ:0,05)

Вариант 2.

1. Игральную кость (кубик) бросили один раз. Какова вероятность того, что выпало не более 3 очков? (Ответ:0,5)
2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых. (Ответ:0,08)
3. Женя дважды бросает игральный кубик. В сумме у нее выпало 5 очков. Найдите вероятность того, что при первом броске выпало 2 очка. (Ответ:0,25)
4. Маша и Даша играют в кости. Они бросают игральную кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 11 очков. Найдите вероятность того, что Маша выиграла. (Ответ:0,5)
5. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 17 очков. Результат округлите

VI. Домашняя работа

1. В случайном эксперименте бросают три игральные кости. В сумме выпало 12 очков. Найдите вероятность того, что при первом броске выпало 5 очкаов Результат округлите до сотых.
2. Катя трижды бросает игральный кубик. Какова вероятность того, что все три раза выпадут одинаковые числа?

VII. Итог урока

Что нужно знать для нахождения вероятности случайного события?

Для вычисления классической вероятности нужно знать все возможные исходы события и благоприятные исходы.

Классическое определение вероятности применимо только к событиям с равновозможными исходами, что ограничивает область его применения.

Для чего в школе изучаем теорию вероятности?

Многие явления окружающего нас мира поддаются описанию только с помощью теории вероятностей.

Литература

1. Алгебра и начала математического анализа.10-11 классы: учеб. для общеобразовательных учреждений: базовый уровень / [Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.]. – 16-е изд., перераб. – М.: Просвещение, 2010. – 464 с.
2. Семенов А.Л. ЕГЭ: 3000 задач с ответами по математике. Все задания группы В / – 3-е изд., перераб. и доп. – М.: Издательство “Экзамен”, 2012. – 543с.
3. Высоцкий И.Р., Ященко И.В. ЕГЭ 2012. Математика. Задача В10. Теория вероятностей. Рабочая тетрадь /Под ред. А.Л.Семенова и И.В.Ященко. – М.: МЦШМО, 2012. – 48 с.

Таня	Наташа	Сумма очков
Вторая	Третья	Сумма очков