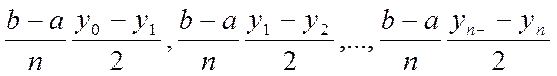 |
7.2. Метод трапеций
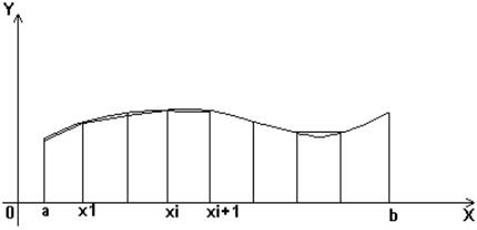
В данном методе (дуга f(x) заменяется хордой CD) (рис. 7.6).
 |
 |
Рис. 7.6. Оценка элементарной площади Si трапецией
Из рисунка 7.6. видно, что 
(7.7)
Погрешность формулы трапеций пропорциональна квадрату шага h 
, т. е. формулы центральных прямоугольников и трапеций имеют близкую точность.
Знак погрешности легко объяснить по геометрической иллюстрации применения формулы.
Блок-схема алгоритма вычисления определенного интеграла методом трапеций
 |
 |
Метод Симпсона
На каждом элементарном отрезке подынтегральная функция f(x) заменяется квадратичной параболой, построенной по трем точкам: концам элементарного отрезка ( 
), ( 
) и его середине ( 
).
Площадь полученной криволинейной трапеции служит оценкой элементарной площади Si:
.
Тогда значение интеграла:
Преобразуем данную формулу:
(7.8)
Формула Симпсона имеет высокую точность, так как погрешность метода dм = О(h 3 ).
 |
Блок-схема алгоритма вычисления определенного интеграла методом Симпсона.
Точность и сходимость методов прямоугольников, трапеций, Симпсона
Формулы для оценки погрешности численного интегрирования методом:
; (7.9)
; (7.10)
, (7.11)
где 
Формула Симпсона обладает повышенной точностью, т. к.:
1) она оказывается точной для 
являющихся полиномами до третьей степени включительно, т. к. для этих случаев производная четвертого порядка равна нулю;
2) для достижения той же точности, что и в формуле трапеций, в формуле Симпсона можно брать меньшее число 
отрезков разбиения.
Задание
Вычислить определенный интеграл методами:
Варианты заданий:
| № Вар. | Подынтег- ральная функция | Интервал интег- рирования [a, b] | Кол-во частей разбие-ния: n1, n2, n3 | Первообразная функция F(x) |
 |
[2;5] | 40, 80, 200 |  |
|
 |
[3;7] | 80, 150, 400 |  |
|
 |
[0,9;3,1] | 20, 100, 500 |  |
|
 |
[0,2;  ] |
50, 180, 400 |  |
|
 |
[0,8;1,9] | 50, 200, 1000 |  |
|
 |
[1;5] | 30, 500, 1200 |  |
|
 |
[2; 6] | 100, 300, 2000 |  |
|
 |
[1;3] | 50, 400, 2500 |  |
|
 |
[0,8;4,5] | 25,150, 1000 |  |
|
 |
[2;3] | 40, 300, 2000 |  |
|
 |
[1,7;3,2] | 50, 250, 500 | -2·1n(  ) |
|
 |
[2,1;4,2] | 80, 300, 2000 |  |
|
 |
[3;5] | 50, 500, 4000 |  |
|
 |
[2;3,1] | 40, 200, 5000 |  |
|
 |
[2;4] | 60, 180, 3500 |  |
Контрольные вопросы
1. Объяснить геометрический смысл определенного интеграла.
2. Какой зависимостью связан шаг интегрирования с количеством интервалов?
3. Какой из методов вычисления определенного интеграла является самым точным и как это определяется?
Кафедра Информатики
Разработка приложения: «Исследование методов Симпсона(парабол) и трапеции»
К курсовой работе
по «Информатика»
| 1308.301406.000ПЗ |
| (обозначение документа) |
| Группа | Фамилия, И., О. | Подпись | Дата | Оценка |
| МА-178 | ||||
| Студент | Хибатов Г.Я. | |||
| Консультант | Адгамова Г. Х. | |||
| Принял | Адгамова Г.Х. |
Уфа 2013 г.
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
на курсовой(ую) проект (работу) по дисциплине
Студент Хибатов Галинур Явдатович Группа МА-178
фамилия, имя, отчество № акад. гр.
1. Тема курсового(ой) проекта (работы)
Разработка приложения: «Исследование методов Симпсона(парабол) и трапеции»
2. Основное содержание: Решение определенного интеграла методами трапеции и Симпсона, исследование погрешностей методов вычисления.
3. Требования к оформлению:
3.1. Пояснительная записка должна быть оформлена в редакторе MS Word
в соответствии с требованиями ГОСТ 2.105-95 ЕСКД, ГОСТ 19.701-90 ЕСПД,
ЕСКД, ЕСПД, ГОСТ, др.
ГОСТ Р 7.0.5-2008, СТО УГАТУ 016 – 2007
3.2. Графическая часть должна содержать:
Экранные формы реализованного интерфейса приложения.
Блок-схемы алгоритмов используемых методов
Дата выдачи «» 2012 г. Дата окончания «» 2012 г.
Руководитель / Адгамова Г. Х. /
Описание методов 4
Метод трапеции. 4
Метод Симпсона (парабол) 7
Составные части программы 9
Титульный лист программы.. 9
Главная форма программы.. 10
Form3.Визуализация метода. 11
Form4. Разработчик. 12
Form5. Исследование методов. 13
Form6. Блок-схема метода Симпсона. 14
Form7. Блок-схема метода трапеции. 15
Form8. О программе. 16
Список литературы 17
Текст программы.. 18
Введение
Данная программа предназначена для исследования методов вычисления определенных интегралов, а именно метода Симпсона (парабол)
и метода трапеции. Точное значение интеграла вычисляется по формуле Ньютона-Лейбница, показывается график зависимости погрешностей от числа разбиений, также представлена визуализация метода трапеции.
Описание методов
Метод трапеции
Будем исходить из геометрических соображений и рассматривать определенный интеграл ,
как площадь некоторой фигуры, чаще всего ее называют криволинейной трапецией, ограниченной кривой y = f(x), осью Ox и прямыми y = a, y = b. Будем также предполагать, что функция y = f(x) непрерывна на [a. b].
Идея, которая привела к понятию определенного интеграла заключалась в следующем. Разбить всю фигуру на полоски одинаковой ширины dx = (b – a)/n, а затем каждую полоску заменить прямоугольником, высота которого равно какой-либо ординате (см. рис. 48).
Тогда получится следующая формула:
Заменим данную кривую вписанной в нее ломаной, с вершинами в точках (xi, yi),
Тогда криволинейная трапеция заменится фигурой, состоящей из трапеций (см. рис. 49). Будем по-прежнему считать, что промежуток [a, b] разбит на равные части, тогда площади этих трапеций будут равны:
Складывая полученные значения, приходим к приближенной формуле:
Эта приближенная формула называется формулой трапеций.
Блок-схема метода трапеции
МЕТОД РЕШЕНИЯ
Метод трапеций
По условию задачи исходными данными являются пределы интегрирования: a – нижний предел, b – верхний предел; также дано количество интервалов разбиения n.
Допустим, наша подынтегральная функция y = f(x) непрерывна на отрезке [a;b], тогда разобьем отрезок [a;b] на количество интервалов n длины h точками, находящимися внутри отрезка (такие точки также называются узлами), то есть a = x 2 +1;
Высчитываем определенный интеграл по формуле 1.7
Для решения задачи графическим способом прежде всего нам необходим график. Для построения графика установим зависимость координат x от y на отрезке от [0;2] и узла от значения функции в узле в виде таблиц.
| i | ||
| xi | 0,5 | 1,5 |
| f(xi) | 1,25 | 3,25 |
| x |
| y |
Выберем произвольный масштаб графика, построим оси, отметим полученные точки и соединим их, после разобьем график на элементарные отрезки, соединив ближайшие точки.
| f(x1) f(x2) f(x3) f(x4) f(x5) f(xi) f(xi) f(xi) |
Рис 1.2 Пример метода трапеций
Мы получили множество трапеций. Теперь осталось лишь посчитать их площади и сложить.
Ответ при графическом и аналитическом решении совпал. Следовательно метод верный.
Список условных обозначений к блок-схеме алгоритма вычисления интеграла методом трапеций
· a – нижний предел интегрирования;
· b – верхний предел интегрирования;
· n – количество интервалов разбиения;
· h – высота трапеции;
· s – сумма оснований;
1.1.3.Блок-схема алгоритма вычисления интеграла методом трапеций
| Конец |
| i = 1, n-1 |
| x = a + i·h |
| I = s·h/2 |
| Вывод I |
| S = S+2·f(x) |
I w4LXi4ujeem3/uJIB7Z0GxgHBC293fachZizaWt19oZpG9Y6069OwKq93tVBZ5Eicx+JU9LMLPzf jMZRT7wTzvBCLtPMNJ+rhWPf0C1emspFfD9IkJklhxuQXlBkeNm4QasYV89Cxo6Xe89LXe6qbywP s9zSg/648Q6OzFy+2Sovus780usoZxMsu6lgmZQhSO6V4CgTkUX28PwzyvPp0of/AAAA//8DAFBL AwQUAAYACAAAACEARAnHst8AAAAHAQAADwAAAGRycy9kb3ducmV2LnhtbEyPQUvDQBCF74L/YRnB m92ktRpjJqUU9VQEW0G8TZNpEprdDdltkv57x5Me573He99kq8m0auDeN84ixLMIFNvClY2tED73 r3cJKB/IltQ6ywgX9rDKr68ySks32g8edqFSUmJ9Sgh1CF2qtS9qNuRnrmMr3tH1hoKcfaXLnkYp N62eR9GDNtRYWaip403NxWl3NghvI43rRfwybE/HzeV7v3z/2saMeHszrZ9BBZ7CXxh+8QUdcmE6 uLMtvWoR5JGAMI+fQIl7Hy1FOCA8LpIEdJ7p//z5DwAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4 kv4AAADhAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAI AAAAIQA4/SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAI AAAAIQCgxObfjAYAAHYtAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQA BgAIAAAAIQBECcey3wAAAAcBAAAPAAAAAAAAAAAAAAAAAOYIAABkcnMvZG93bnJldi54bWxQSwUG AAAAAAQABADzAAAA8gkAAAAA ">
| Начало |
| Программа для вычисления определенного интеграла |
| Введите пределы интегрирования и количество интервалов разбиения |
| a, b, n |
| h = (b-a)/n |
| S = f(a)+f(b) |
| Рис. 1.3. Блок-схема метода трапеций |
| Конец |
| Рис. 1.3 Блок-схема метода трапеций |
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8792 – 
| 7154 – 
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
