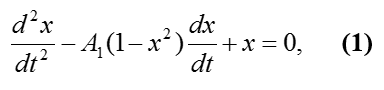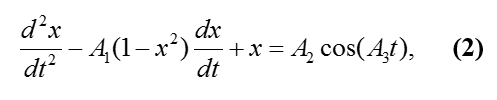Генератор ван дер поля

Операционная система: Windows.
Лицензия: бесплатно.
Версия: 1.1.0.0.
Аннотация: демонстрируется программа по анализу генератора Ван-дер-Поля, позволяющая наблюдать такие состояния системы, как устойчивый аттрактор, устойчивый и неустойчивый фокус, предельный цикл, образование второго неустойчивого фокуса и предельного цикла.
Скачать: ZIP (архив программы).
Ключевые слова: осциллятор Ван дер Поля, уравнение Ван Дер Поля matlab, дифференциальное уравнение Ван дер Поля, уравнение Ван Дер Поля фазовый портрет, метод Ван Дер Поля пример, уравнение генератор Ван Дер Поля, метод Рунге Кутта 2 порядка, уравнение Ван дер Поля портрет, метод Ван дер Поля, осциллятор Ван дер Поля дуффинга, фазовый портрет уравнения Ван-дер-Поля, решение уравнения Ван-дер-Поля, Бальтазар Ван дер Поль, Ван дер Поль математик, Ван дер Поль маткад, Ван дер Поль уравнение, Ван дер Поль нелинейная теория электрических колебаний, Ван дер Поль программа, Ван Дер Поль генераторы, Ван дер Поль матлаб.

Осциллятор Ван-дер-Поля представляет собой генератор с нелинейным затуханием. Был предложен голландским физиком Бальтазаром Ван-дер-Полем. Ван-дер-Поль выявил колебания, позже названные предельными циклами, а также состояние детерминированного хаоса. Осциллятор Ван-дер-Поля задается дифференциальным уравнением

где x – координата точки, зависящая от времени t, A1 – коэффициент, характеризующий силу затухания колебаний. В результате исследования системы были выявлены нижеуказанные закономерности.

При отрицательных значениях A1

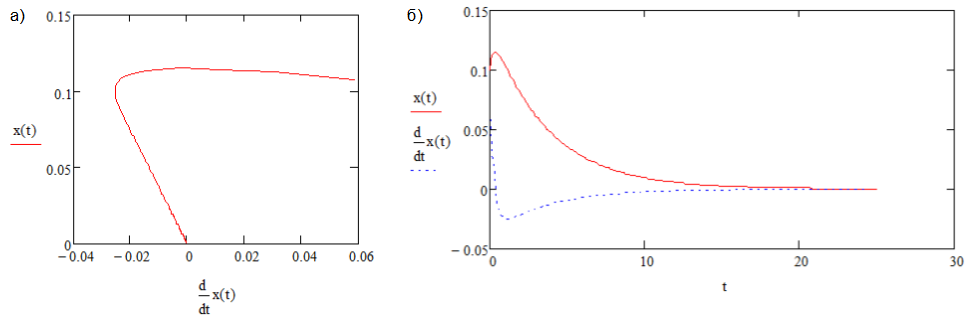
Рис. 1. Устойчивый узел, A1 где x – координата точки, зависящая от времени t, A1 – коэффициент, характеризующий силу затухания колебаний. В результате исследования системы были выявлены нижеуказанные закономерности.

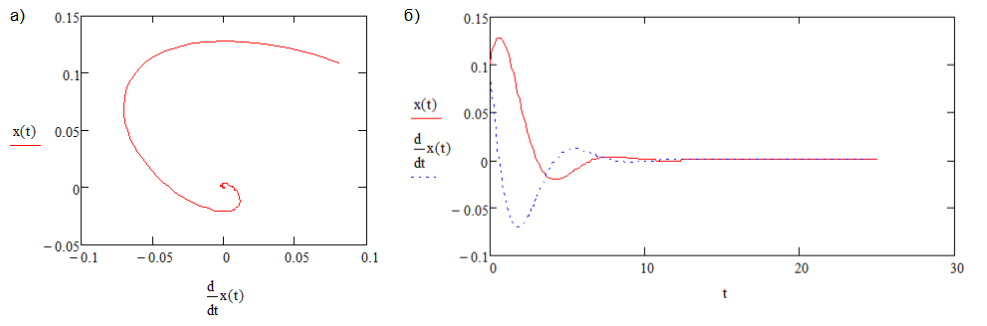
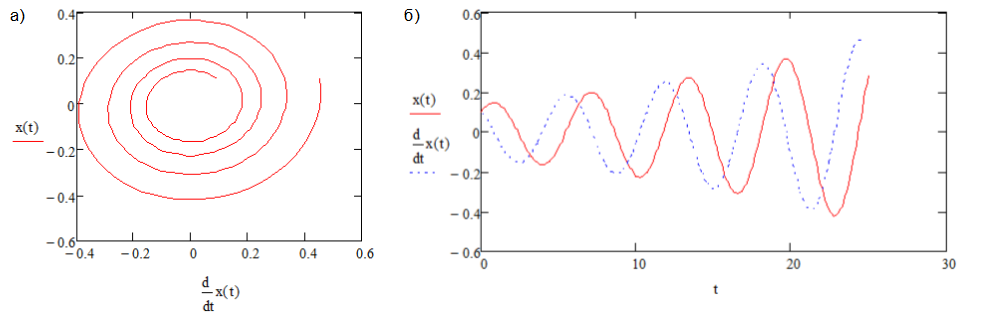
Рис. 2. Устойчивый фокус, A1

Устойчивый предельный цикл (рис.3) образуется при последующем увеличении значения A1, A1

Рис. 3. Устойчивый предельный цикл, A1 Увеличение A1 до положительных значений (A1>0) приводит к потере устойчивости, в результате образуется особая точка вида неустойчивый фокус (рис.4).

Рис. 4. Неустойчивый фокус, A1>0

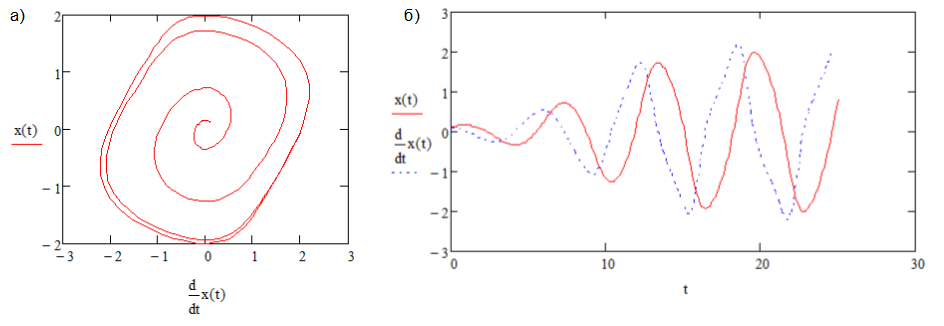
Дальнейшее увеличение A1 (A1>0) приводит к образованию неустойчивого предельного цикла (рис.5).

Рис. 5. Неустойчивый предельный цикл, A1>0

Модернизированный генератор Ван-дер-Поля позволяет наблюдать автоколебательный режим работы системы. В случае модернизированного осциллятора формула (1) преобразуется к виду (2)

где x – координата точки, а A1, A2, A3 – коэффициенты (A2>0, 0

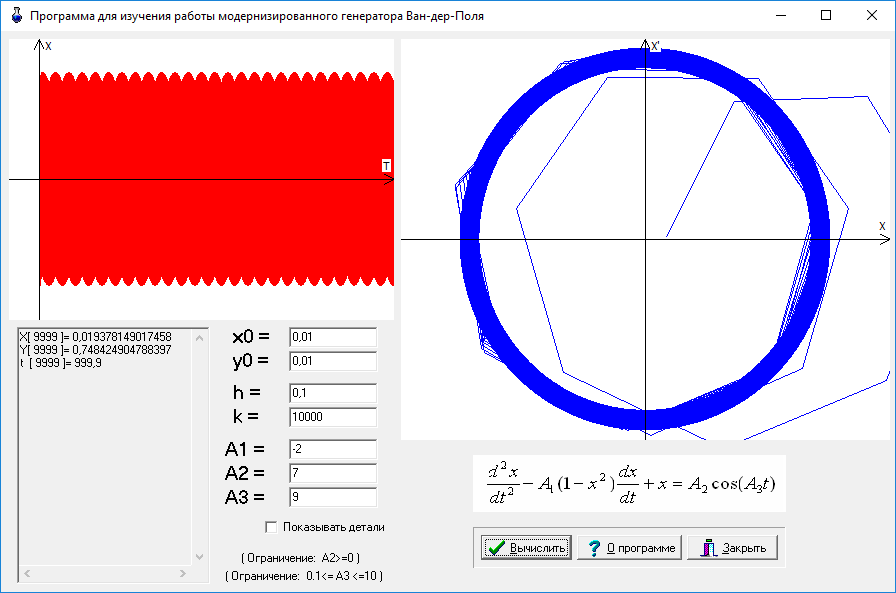
Программа «VanDerPol – программа для изучения работы модернизированного генератора Ван-дер-Поля», реализованная в среде разработки Turbo C++, позволяет смоделировать работу модернизированного генератора Ван-дер-Поля. Построение фазового портрета и графика зависимости решений от времени t ведется на основе метода Рунге-Кутта второго порядка. Интерфейс программы приведен на рис.6.

Рис. 6. Интерфейс программы для изучения работы модернизированного генератора Ван-дер-Поля

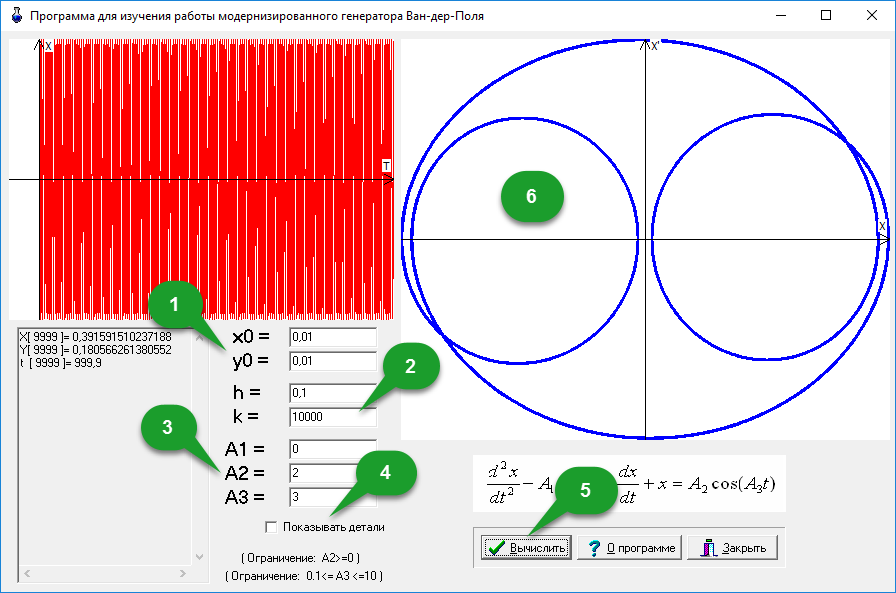
Моделирование работы модернизированного генератора с использованием программы VanDerPol предполагает выполнение следующих шагов (рис.7):

• определить начальные координаты (x0,y0);
• задать шаг интегрирования h и число итераций k;
• установить значение коэффициентов A1, A2, A3;
• (опционально) установить индикатор «Показывать детали» для получения деталей решения;
• нажать кнопку «Вычислить»;
• (опционально) дважды щелкнуть на полученных изображениях для их копирования в буфер обмена.

Рис. 7. Последовательность шагов для запуска программы VanDerPol

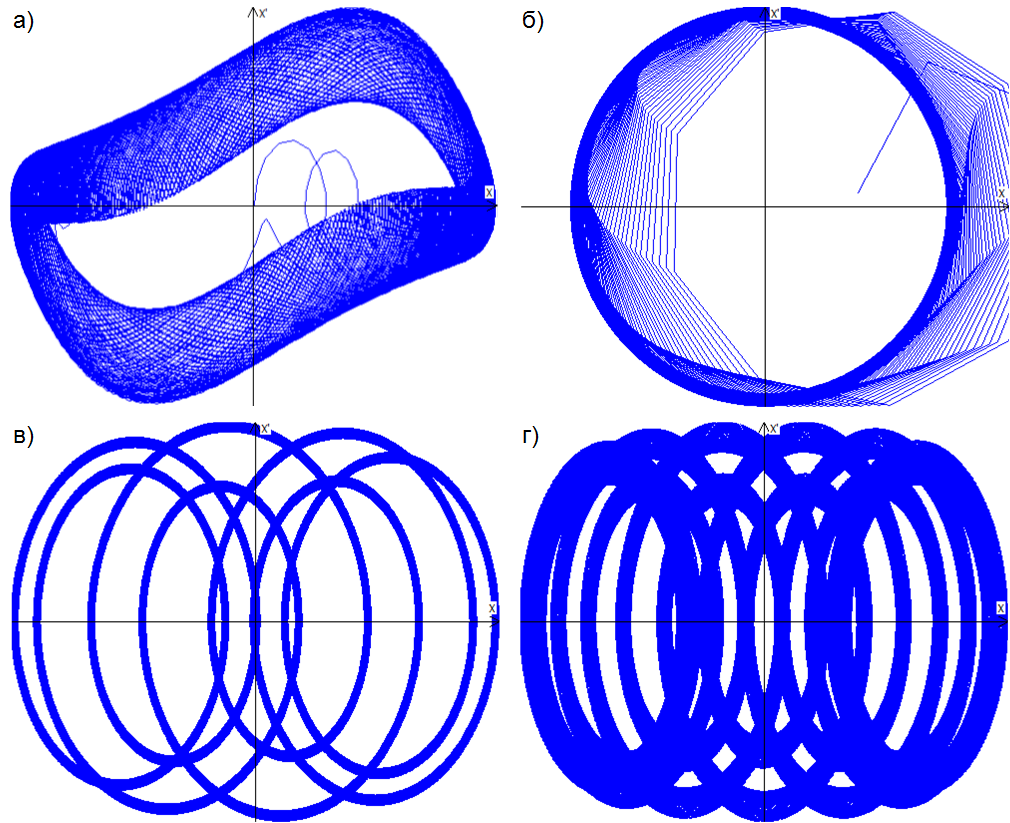
Рис. 8. Примеры фазовых портретов модернизированного генератора Ван-дер-Поля

Операционная система: Windows.
Лицензия: бесплатно.
Версия: 1.1.0.0.
Аннотация: демонстрируется программа по анализу генератора Ван-дер-Поля, позволяющая наблюдать такие состояния системы, как устойчивый аттрактор, устойчивый и неустойчивый фокус, предельный цикл, образование второго неустойчивого фокуса и предельного цикла.
Скачать: ZIP (архив программы).
Ключевые слова: осциллятор Ван дер Поля, уравнение Ван Дер Поля matlab, дифференциальное уравнение Ван дер Поля, уравнение Ван Дер Поля фазовый портрет, метод Ван Дер Поля пример, уравнение генератор Ван Дер Поля, метод Рунге Кутта 2 порядка, уравнение Ван дер Поля портрет, метод Ван дер Поля, осциллятор Ван дер Поля дуффинга, фазовый портрет уравнения Ван-дер-Поля, решение уравнения Ван-дер-Поля, Бальтазар Ван дер Поль, Ван дер Поль математик, Ван дер Поль маткад, Ван дер Поль уравнение, Ван дер Поль нелинейная теория электрических колебаний, Ван дер Поль программа, Ван Дер Поль генераторы, Ван дер Поль матлаб.

Осциллятор Ван-дер-Поля представляет собой генератор с нелинейным затуханием. Был предложен голландским физиком Бальтазаром Ван-дер-Полем. Ван-дер-Поль выявил колебания, позже названные предельными циклами, а также состояние детерминированного хаоса. Осциллятор Ван-дер-Поля задается дифференциальным уравнением

где x – координата точки, зависящая от времени t, A1 – коэффициент, характеризующий силу затухания колебаний. В результате исследования системы были выявлены нижеуказанные закономерности.

При отрицательных значениях A1

Рис. 1. Устойчивый узел, A1 где x – координата точки, зависящая от времени t, A1 – коэффициент, характеризующий силу затухания колебаний. В результате исследования системы были выявлены нижеуказанные закономерности.

Рис. 2. Устойчивый фокус, A1

Устойчивый предельный цикл (рис.3) образуется при последующем увеличении значения A1, A1

Рис. 3. Устойчивый предельный цикл, A1 Увеличение A1 до положительных значений (A1>0) приводит к потере устойчивости, в результате образуется особая точка вида неустойчивый фокус (рис.4).

Рис. 4. Неустойчивый фокус, A1>0

Дальнейшее увеличение A1 (A1>0) приводит к образованию неустойчивого предельного цикла (рис.5).

Рис. 5. Неустойчивый предельный цикл, A1>0

Модернизированный генератор Ван-дер-Поля позволяет наблюдать автоколебательный режим работы системы. В случае модернизированного осциллятора формула (1) преобразуется к виду (2)

где x – координата точки, а A1, A2, A3 – коэффициенты (A2>0, 0

Программа «VanDerPol – программа для изучения работы модернизированного генератора Ван-дер-Поля», реализованная в среде разработки Turbo C++, позволяет смоделировать работу модернизированного генератора Ван-дер-Поля. Построение фазового портрета и графика зависимости решений от времени t ведется на основе метода Рунге-Кутта второго порядка. Интерфейс программы приведен на рис.6.

Рис. 6. Интерфейс программы для изучения работы модернизированного генератора Ван-дер-Поля

Моделирование работы модернизированного генератора с использованием программы VanDerPol предполагает выполнение следующих шагов (рис.7):

• определить начальные координаты (x0,y0);
• задать шаг интегрирования h и число итераций k;
• установить значение коэффициентов A1, A2, A3;
• (опционально) установить индикатор «Показывать детали» для получения деталей решения;
• нажать кнопку «Вычислить»;
• (опционально) дважды щелкнуть на полученных изображениях для их копирования в буфер обмена.

Рис. 7. Последовательность шагов для запуска программы VanDerPol

Рис. 8. Примеры фазовых портретов модернизированного генератора Ван-дер-Поля

Федеральное агентство по образованию ГОУ ВПО
«Саратовский государственный университет имени Н.Г. Чернышевского»

Кафедра электроники,
колебаний и волн

Генератор Ван-дер-Поля как пример динамической
системы с непрерывном временем.

Курсовая работа

студента 1 курса факультета нелинейных процессов
Мальцева Александра Викторовича

Научный руководитель,
доцент КЭКиВ ФНП СГУ, к.ф.-м.н., ______________А.А. Короновский

Заведующий кафедрой,
чл.-кор. РАН, проф.,
д. ф.-м. н. _______________Д. И. Трубецков

1. Определение периодических автоколебаний…………. 4

2. Генератор Ван-дер-Поля………………………………. 8

3. Зависимость формы автоколебаний от параметров
системы………………………………………………………10

Список литературы………………………………………. 18

Введение.
В современном мире большинство окружающих нас в природе и

технике нелинейных динамических систем в общем случае

неконсервативно. Практически в любой системе имеются потери

(излучение, трение, нагрев и т.д.), и обычно система не является

энергетически изолированной: на нее действуют различные

внешние силы и поля, как статические, так и переменные. Какие

принципиально новые (по сравнению с консервативными

системами) явления возникают в диссипативных системах, в

которых колебательная энергия может не только дисспировать

из-за потерь, но и пополняться из-за неустойчивостей,

связанных с неравновесностью системы?

Самое важное и замечательное среди таких явлений —

генерация незатухающих колебаний, свойства которых не

зависят от того, когда и из какого начального состояния была

запущенна система, т. е. незатухающих колебаний, устойчивых
0 0
1 Fкак по отно шению к внешним возмущениям, так и к

изменению начальных условий. Системы, обладающие

свойством генерировать такие колебания, А.А.Андронов полвека

назад назвал автоколебательными, впервые придав им четкое

математическое содержание, связав автоколебания с

предельными циклами Пуанкаре, а самые первые шаги в этой

области были сделаны самим Ван-дер-Полем и Эпплтоном.

Актуальность заключается еще и в том, что на базе системы

Ван-дер-Поля можно создать ряд компьютерных, теоретических
0 0
1 Fи экспериментальных моделей, демонстри рующих новые

особенности динамики.

Моя задача в курсовой работе заключается в ознакомлении с

динамическими системами с непрерывным временем на

примере генератора Ван-дер-Поля с мягким режимом

возбуждения, а так же визуализация различных генераторов Ван-

дер-Поля, в зависимости от характеристики системы.

1. Определение периодических автоколебаний.
Предельный цикл — замкнутая фазовая траектория, к которой

стремятся все соседние траектории, — является образом
0 0
1 Fпериодичес ких автоколебаний, о которых мы и будем говорить

0 0
1 Fв этой главе. Авто колебания в динамической системе могут

0 0
1 Fбыть не только периодичес кими, но и квазипериодическим и

даже стохастическими. Поэтому сначала мы дадим достаточно

общее определение.

Автоколебания — это незатухающие колебания,

поддерживаемые внешними источниками энергии в нелинейной

диссипативной системе, вид и свойства которых определяются

самой системой и не зависят от начальных условий (по крайней

мере, в конечных пределах).

Автоколебания принципиально отличаются от других
0 0
1 Fколебатель ных процессов в диссипативных системах тем, что

0 0
1 Fдля их поддержа ния, вообще говоря, не требуется

периодических воздействий извне.[3]

Колебания скрипичной струны при равномерном движении

смычка, колебания тока в радиотехническом генераторе,

колебания воздуха в органной трубе, маятника в «ходиках» —

хорошо известные примеры автоколебаний. В простейших
0 0
1 Fавтоколебательных системах, или «авто генераторах», обычно

0 0
1 Fможно выделить колебательную систему с зату ханием,

усилитель, нелинейный ограничитель — звено «обратной
0 0
1 Fсвя зи». Это можно сделать, например, в классическом

генераторе Ван-дер-Поля (рис. 1а, б). Автоколебания в таком
0 0
1 Fгенераторе устанавлива ются следующим образом: случайно

возникшие в LС-контуре малые колебания через катушку L’
0 0
1 Fуправляют анодным током лампы, кото рый (при

соответствующем взаимном расположении L и L’) усиливает

колебания в контуре. При условии, что потери в контуре меньше,

чем вносимая в контур, таким образом, энергия, амплитуда
0 0
1 Fколебаний в кон туре нарастает.

Рис. 1. Схемы генераторов Ван-дер-Поля: а – с контуром в цепи анода; б –

с контуром в цепи сетки; в – характеристика лампы, аппроксимированная

кубическим полиномом.

С увеличением амплитуды колебаний вследствие нелинейной
0 0
1 Fза висимости анодного тока от напряжения на сетке лампы

поступающая в контур энергия уменьшается и при некоторой

амплитуде колебаний сравнивается с потерями. В результате

устанавливается режим стационарных периодических

колебаний, в котором все потери энергии компенсирует анодная

Таким образом, для установления автоколебаний

принципиальна нелинейность, которая управляет

поступлением и потерями энергии источника. Частотные же

характеристики источника принципиальной роли не играют.

Автоколебания тем и отличаются от собственных колебаний,
0 0
1 Fчас тота которых определяется параметрами системы, а

амплитуда и фаза — начальными условиями, и от вынужденных
0 0
1 Fколебаний, амплиту да, фаза и частота которых определяются

0 0
1 Fвнешней силой, что их ам плитуда и частота определяются

0 0
1 Fтолько параметрами системы и не за висят от начальных

условий, а фаза не существенна. (Характеристики источника,

естественно, влияют на параметры системы.)[2]

Рис. 2 Фазовые портреты автоколебательных систем: а — «мягкое»
0 0
1 Fвоз буждение; б — «жесткое» возбуждение (начальная точка на фазовой

0 0
1 Fплос кости должна лежать вне заштрихованной области; 1 и 2 —

устойчивый и неустойчивый предельные циклы)

Рассмотренный нами применительно к генератору Ван-дер-Поля

режим возникновения автоколебаний, не требующий начального
0 0
1 Fтолч ка, называется режимом «мягкого» возбуждения. Для

0 0
1 Fгенераторов с од ной степенью свободы такому режиму

соответствует фазовый портрет, представленный на рис. 2 а .
0 0
1 FВстречаются также системы с «жест ким» возбуждением

автоколебаний. Это такие системы, в которых 0 01 Fколе бания

самопроизвольно нарастают с некоторой начальной амплитуды.

Для перехода систем с жестким возбуждением в режим

стационарной генерации необходимо начальное возбуждение с

амплитудой, большей некоторого критического значения.

Фазовый портрет такого генератора приведен на рис. 2.б .
0 0
1 FВидно, что для выхода траектории на устой чивый предельный

цикл начальная точка на фазовой плоскости 0 01 Fдолж на лежать вне

области притяжения устойчивого состояния равновесия. Отсюда

ясен и физический смысл неустойчивых предельных циклов:

они служат границей между областями начальных условий, из

которых система стремится к различным устойчивым режимам

движения (на фазовой плоскости таким движениям

соответствуют притягивающие множества — аттракторы,

например устойчивые состояния равновесия или предельные

циклы). Размеры предельного цикла определяют амплитуду

автоколебаний генератора, время движения изображающей
0 0
1 Fточки по циклу — их пери од, а форма предельного цикла —

форму колебаний. Таким образом, 0 01 Fза дача об исследовании

периодических автоколебаний в 0 01 Fсистеме сводит ся к задаче

нахождения предельных циклов в фазовом пространстве и

определения их параметров. Общий метод для нахождения

предельных циклов (как, например, для определения координат

и типов состояний равновесия) не известен даже для систем

второго порядка. Правда, на основании теории индексов

Пуанкаре мы можем 0 01 Fсформули ровать некоторые критерии

отсутствия предельных циклов на фазовой плоскости; например,

если в системе нет состояний равновесия, то в ней не может

быть и предельных циклов, или если единственное состояние

равновесия является седлом, то предельных циклов тоже нет и

2. Генератор Ван-дер-Поля.

Теперь рассмотрим генератор Ван-дер-Поля. Схема генератора

Ван-дер-Поля (рис 1. б) и описывающее ее уравнение Ван-дер-

И сейчас, спустя полвека после появления, служат основной

моделью автоколебаний с одной степенью свободы. Для

уравнения (1) и для уравнения Рэлея

которое после дифференцирования и замены переменной
0 0
1 Fприни мает вид (1), существование предельных циклов

доказать сравнительно просто.

Уравнение Ван-дер-Поля легко получить для лампового
0 0
1 Fгенерато ра, например, с колебательным контуром в цепи сетки,

принципиальная схема которого изображена на рис. 1 б. Будем
0 0
1 Fпренебрегать сеточны ми токами. На основании законов

Кирхгофа для колебательного контура Величина есть ЭДС,

которая наводится в контуре под воздействием на него анодного

тока , протекающего по катушке в цепи анода (слагаемое можно

назвать ЭДС обратной связи). Из написанных уравнений
0 0
1 Fследу ет, что

где крутизна характеристики лампы в пренебрежении анодной

реакцией (предполагается, что анодный ток зависит лишь от U,

поэтому Уравнение (3) есть нелинейное уравнение
лампового генератора. 0 01 FПредпо ложим далее, что анодно-

0 0
1 Fсеточную характеристику лампы можно ап проксимировать

полиномом (рис. 1 в ). Это означает, , и уравнение (3)

принимает вид (1), где

Величина параметра показывает, насколько сильно возбужден
0 0
1 Fгенера тор (при

Величина 0 01 Fхарак теризует амплитуду автоколебаний: чем
меньше , 0 01 Fтем больше ампли туда. Вводя безразмерные

переменные и параметры, , получим окончательно

3.Зависимость формы автоколебаний от

параметров системы.
Как будет зависеть форма предельного цикла от параметра ? При

= О система становится линейной консервативной.

Естественно ожидать, что при малом автоколебания будут
мало отличаться от гармонических колебаний, а нелинейное

0 0
1 Fтрение лишь «выбирает» ампли туду устойчивого предельного

цикла. При больших форма колебаний может существенно

отличаться от синусоидальной.

Одним из методов нахождения предельных циклов является
0 0
1 Fме тод графического построения интегральных кривых на

0 0
1 Fфазовой плос кости — метод изоклин. Изоклиной называется

геометрическое место точек, в которых касательные к
0 0
1 Fинтегральным кривым имеют одинако вый наклон. Запишем

уравнение (5) в виде Уравнение интегральных кривых

Пусть наклон интегральной кривой в некоторой точке М0(хо, у0)
0 0
1 Fра вен K , т. е. Тогда из (6) получим:

Если х = 0, то k=, т. е. ось у пересекается интегральными
кривыми под тем большим углом, чем больше . При у = 0

0 0
1 Fкасательные к интег ральным кривым вертикальны. Давая k

различные значения, из (7) будем получать уравнения разных

изоклин [4]Строя затем семейства изоклин, можно построить

интегральные кривые, а, следовательно, и фазовые траектории.
0 0
1 FФазовые портреты, получен ные таким методом для уравнения

(5) при различных значениях , изображены на рис.3. На рис. 4
0 0
1 Fприведены осциллограммы, ил люстрирующие характер

0 0
1 Fустановления и форму автоколебаний в сис теме.

Рис. 3 Фазовые портреты, соответствующие уравнению (5) при различных

значениях параметра нелинейности µ, в координатах (, ): квазигармонические

колебания µ= -0,1 – а), µ = 0,01 – б), µ =0,2 – в) ]

сильно несинусоидальные колебания µ=1 – г)

Предельные циклы на рис. 3 содержат внутри особую точку,

причем для эта точка является неустойчивым фокусом, а для
неустойчивым узлом. Форма автоколебаний при этом меняется

от квазисинусоидальной до релаксационной. Величина
0 0
1 Fха рактеризует нелинейность в системе таким образом: чем

0 0
1 Fбольше нели нейность в системе, тем больше форма колебаний

о ней отличается от синусоидальной. В физической литературе
0 0
1 Fвеличину иногда называ ет прочностью предельного цикла

— при малом . траектории слабо притягиваются к циклу, при

такое притяжение очень сильно,

Рис. 4 Осциллограммы, иллюстрирующие характер установления и форму

автоколебаний в системе, описываемой уравнением (5). Они соответствуют

фазовым портретам на рис. (3): µ= -0,1 – а), µ = 0,01 – б), µ =0,2 – в) , µ=1 – г)

т. е. цикл «прочный». В случаях удается достаточно просто
решить задачу об автоколебаниях в системе приближенными

аналитическими методами.

Заключение.
В своей курсовой работе я ознакомился с динамическими

системами с непрерывным временем на примере генератора

Ван-дер-Поля с мягким режимом возбуждения, визуализовал

различные генераторы Ван-дер-Поля, в зависимости от

характеристики системы. А так же проработал достаточное

количество книг по генератору Ван-дер-Поля и понял, что самое

важное, нужное и замечательное среди таких систем — это

генерация незатухающих колебаний, свойства которых не

зависят от того, когда и из какого начального состояния была

запущенна система, то есть незатухающих колебаний,
0 0
1 Fустойчивых как по отно шению к внешним возмущениям, так

и по отношению к изменению начальных условий. Системы,

обладающие этим замечательным свойством: генерировать такие

колебания А. А. Андронов полвека назад назвал

автоколебательными, впервые придав им четкое математическое

содержание, связав автоколебания с предельными циклами

Пуанкаре, а самые первые шаги в этой области были сделаны в

исследованиях Ван-дер-Поля и Эпплтона. Так же необходимо

отметить, что изучение данной системы будет

совершенствоваться как с теоретическо-экспериментальной

стороны, так и со стороны более совершенных компьютерных

моделей. Другими словами, с развитием компьютерных
0 0
1 Fмето дов, теории и экспериментальной техники будут

развиваться и системы, таким образом, исследуемые системы

будут более точно качественно и количественно описываться,

что естественно улучшит результаты исследований. А это в свою

очередь поможет описывать все больше и больше реальных

систем, а они как известно, в общем случае неконсервативные, в

главное это описание будет более точным и верным.

Список литературы.

1. Рабинович М. И., Трубецков Д. И.

Введение в теорию колебаний и волн . – НИЦ «Регулярная

и хаотическая динамика». – 2000г.

2. Андронов А. А., Витт А. А., Хайкин С. Э.

Теория колебаний . – М.: Физматгиз, 1963г.

3. Найфе А. Х.

Методы возмущений . – М.: Мир, 1976г.

4. Кузнецов А.П., Милованов СВ., Тюрюкина Л.В.
0 0
1 FСинхронизация в автоколеба тельной системе с

бифуркацией слияния устойчивого и неустойчивого

циклов – Образование и наука в ГосУНЦ «Колледж».

Саратов: Изд-во ГосУНЦ

«Колледж», 2003. С. 99-108.

","canEdit":false,"canDelete":false,"canReport":false,"canReview":false,"averageShapeVotes":null,"averageStatsVotes":<"1":0,"2":0,"3":0,"4":1,"5":1>,"reviewsCount":2,"averageVotes":"4.5","userVote":null,"previewLimit":3,"advEnabled":true,"totalVotes":null,"title":"u0413u0435u043du0435u0440u0430u0442u043eu0440 u0412u0430u043d-u0434u0435u0440-u041fu043eu043bu044f u043au0430u043a u043fu0440u0438u043cu0435u0440 u0434u0438u043du0430u043cu0438u0447u0435u0441u043au043eu0439 u0441u0438u0441u0442u0435u043cu044b u0441 u043du0435u043fu0440u0435u0440u044bu0432u043du043eu043c u0432u0440u0435u043cu0435u043du0435u043c u043au0443u0440u0441u043eu0432u0430u044f u043fu043e u0444u0438u0437u0438u043au0435 , u0414u0438u043fu043bu043eu043cu043du0430u044f u0438u0437 u0424u0438u0437u0438u043au0430","isPremiumEnabled":false,"hasQuizcardSet":null,"alreadyDownloaded":false,"reviews":