Геометрическая интерпретация симплекс метода

Геометрическая интерпретация симплексного метода

В гл. 3 рассмотрены основные теоремы линейного программирования, из которых следует, что если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает по крайней мере с одним из допустимых базисных решений системы ограничений (см. теоремы 3.3, 3.4). Там же был указан путь решения любой задачи линейного программирования: перебрать конечное число допустимых базисных решений системы ограничений и выбрать среди них то, на котором функция цели принимает оптимальное решение. Геометрически это соответствует перебору всех угловых точек многогранника решений. Такой перебор в конце концов приведет к оптимальному решению (если оно существует), однако его практическое осуществление связано с огромными трудностями, так как для реальных задач число допустимых базисных решений хотя и конечно, но может быть чрезвычайно велико.

Число перебираемых допустимых базисных решений можно сократить, если проводить перебор не беспорядочно, а с учетом изменений линейной функции, т.е. добиваясь того, чтобы каждое следующее решение было "лучше" (или по крайней мере "не хуже"), чем предыдущее, по значениям линейной функции (увеличение ее при отыскании максимума F → шах, уменьшение – при отыскании минимума F → min).

Такой перебор позволяет сократить число шагов при отыскании оптимума. Поясним это на графическом примере.

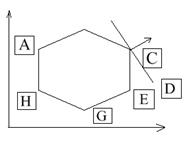
Пусть область допустимых решений изображается многоугольником ABCDEGH (рис. 5.1). Предположим, что его угловая точка А соответствует исходному допустимому базисному решению. При беспорядочном переборе пришлось бы

испытать семь допустимых базисных решений, соответствующих семи угловым точкам многоугольника. Однако из чертежа видно, что после вершины А выгодно перейти к соседней вершине В, а затем к оптимальной точке С.

Вместо семи перебрали только три вершины, последовательно улучшая линейную функцию.

Идея последовательного улучшения решения легла в основу универсального метода решения задач линейного программирования – симплексного [1] метода.

Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений (называемой первоначальной) к соседней, в которой линейная функция принимает лучшее (по крайней мере не худшее) значение (по отношению к цели задачи), до тех пор пока не будет найдено оптимальное решение – вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум).

Впервые симплексный метод был предложен американским ученым Дж. Данцигом в 1949 г., однако еще в 1939 г. идеи метода были разработаны российским ученым Л. В. Канторовичем.

Симплексный метод, позволяющий решить любую задачу линейного программирования, универсален. В настоящее время он используется для компьютерных расчетов, однако несложные примеры с применением симплексного метода можно решить и вручную.

Для реализации симплексного метода – последовательного улучшения решения – необходимо освоить три основных элемента:

• • способ определения какого-либо первоначального допустимого базисного решения задачи;
• • правило перехода к лучшему (точнее, не худшему) решению;
• • критерий проверки оптимальности найденного решения.

Для использования симплексного метода задача линейного программирования должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена в виде уравнений. Алгоритм конкретной вычислительной реализации этих элементов рассмотрим на примерах.

[1]Симплекс (лат. simplex – простой) – простейший выпуклый многогранник в я-мерном пространстве с п + 1 вершиной (например, тетраэдр в 3-мерном пространстве); симплексом является также область допустимых решений неравенства вида •.

На основании материала, рассмотренного выше, сделаем следующие выводы.

1) Область допустимых решений ЗЛП является выпуклым множеством с конечным числом угловых точек, т.е. многогранником или многоугольным множеством.

2) Существует такая угловая точка многогранника решений, в которой линейная функция достигает своего наименьшего (наибольшего) значения.

3) Каждой угловой точке многогранника решений соответствует опорный план, каждый из которых определяется системой m линейно независимых векторов, содержащихся в данной системе из n векторов A₁,A₂. A_n.

Напомню, что опорным планом называется допустимое (если оно содержит лишь неотрицательные компоненты) базисное решение, т.е. если векторы A_i (i=1,2. m), входящие в разложение A₁x₁+A₂x₂+…+A_nx_n = B с положительными коэффициентами x_i, являются линейно независимыми.

Для отыскания оптимального плана необходимо исследовать только опорные планы. Геометрически это соответствует перебору всех угловых точек многогранника решений. Верхняя граница количества опорных планов, содержащихся в данной задаче, определяется числом сочетаний .

Число перебираемых опорных планов можно сократить, если производить перебор не беспорядочно, а с учетом изменений линейной функции, т.е. добиваясь того, чтобы каждое следующее решение было ”лучше” (или, по крайней мере, ”не хуже”), чем предыдущее, по значениям линейной функции (увеличение ее при отыскании максимума, уменьшение – при отыскании минимума).

Такой перебор позволяет сократить число шагов при отыскании оптимума. Поясним это на графическом примере. Пусть область допустимых решений изображается многоуголь­ником ABCDEGH. Предположим, что его угловая точка А соответствует исходному допустимому базисному решению. При беспорядочном переборе пришлось бы испытать 7 допустимых базисных решений, соответствующих семи угловым точкам мно­гоугольника. Однако из чертежа видно, что после вершины А выгодно перейти к вершине В, а затем – к оптимальной точке С, т.е. перебрать только три вершины.

Схема, позволяющая осуществлять упорядоченный переход от одного опорного плана к другому, т.е. исходя из известного опорного плана задачи, за конечное число шагов получить ее оптимальный план, легла в основу универсального метода решения ЗЛП —симплексного метода. Если исходная задача не имеет такого плана или ее линейная функция не ограничена на многограннике решений, то симплексный метод позволяет установить это в процессе решения. Название метода произошло от понятия ”симплекс" (лат. simplex – простой) – простейший выпуклый много­гранник в n-мерном пространстве с n+1 вершиной (например, тетраэдр в 3-мерном пространстве).

Геометрический смысл симплексного метода состоит в последо­вательном переходе от одной вершины многогранника ограничений, называемой первоначальной, к соседней, в которой линейная функция принимает лучшее (по крайней мере, не худшее) значение по отношению к цели задачи, до тех пор, пока не будет найдено оптимальное решение – вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум).

Для реализации симплексного метода – последовательного улучшения решения – необходимо освоить три основных элемента:

• способ определения какого-либо первоначального опорного плана задачи;

• правило перехода от одного опорного плана к другому, на котором значение целевой функции ближе к оптимальному;

• критерий проверки оптимальности найденного плана, позволяющий своевременно прекратить перебор решений на оптимальном решении или сделать заключение об отсутствии решения.

Алгоритм симплекс-метода

Рассмотрим следующую ЗЛП.

Найти максимум целевой функции L=С+ 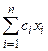® max

при ограничениях где x_j ³ 0 (j=1,2,…,n), b_i ³ 0 (i=1,2,…m; m£n).

1. Приводим систему ограничений к виду, в котором какие-либо m переменных выражены через остальные, причем свободные члены этих выражений были неотрицательными, иначе говоря, разрешаем систему относительно какого-либо исходного базиса.

Предположим, для определенности, что система ограничений задачи содержит т единичных векторов, причем без ограничения общности можно по­ложить, что единичными являются первые т векторов, и, следовательно, переменные, которые выражены через остальные, – это x₁,x₂. x_m, т.е. система ограничений имеет вид:

(1)

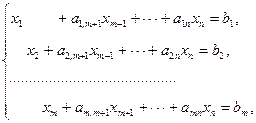
Далее приведем систему к следующему виду

(3),

где все свободные члены b_i ³ 0, (i=1,2. m).

Переменные x₁,x₂. x_m, находящиеся в левой части системы (3), называются базисными, а весь набор ₁,x₂. x_m> – базисом; остальные переменные называются небазисными или свободными. Т.о. мы выразили базисные переменные через свободные.

2. Выражаем целевую функцию L через свободные переменные x_m+1. x_n, подставляя в L вместо базисных переменных их выражения через свободные из (3), и получаем первоначальный опорный план. Получим:

Т.к. все величины х_i (i=1,2,…,n) должны быть неотрицательны, то наименьшие возможные значения свободных переменных – это значения, равные нулю. Положим все свободные переменные равными нулю: x_m+1 = 0, . , x_n = 0

и найдем из системы (3) значения базисных переменных:

Получим первоначальное базисное решение (опорный план) системы, отвечающее базису x₁,x₂. x_m:

Оно будет вследствие (2) допустимым, а т.к. векторы, соответствующие базисным переменным, линейно независимы, то и опорным. Т. е. получим первоначальный опорный план. Геометрически данный план соответствует первоначальной угловой точке.

Подставим в максимизируемую целевую функцию L из (4) значения свободных переменных. Т.к. x_m+1 = 0, . , x_n = 0, то L_б = C.

Посмотрим, можем ли мы улучшить решение, т.е. увеличить целевую функцию L, увеличивая какие-нибудь из переменных x_m+1, . , x_n (уменьшать их мы не можем, т.к. они все равны нулю, а отрицательные значения переменных недопустимы). Это можно осуществить, перейдя к такому новому допустимому решению, в котором эта переменная будет базисной, а не равняться 0 как свободная.

Если оказалось, что все коэффициенты C¢_m+1. C¢_n в (4) отрицательны, то, увеличивая какие-то из переменных x_m+1. x_n сверх нуля, мы не можем увеличить L; значит, найденное нами базисное решение X=(b₁,b₂. b_m,0. 0) оптимально.

3. Пусть среди коэффициентов, упомянутых в предыдущем пункте, т.е. среди чисел C¢_m+1. C¢_n имеются положительные, то увеличивая те из переменных x_m+1, . , x_n, коэффициенты при которых положительны, мы можем улучшить решение, т.е. увеличить L.

Для определенности в такой ситуации будем выбирать переменную, имеющую больший коэффициент. Пусть, например, это будет коэффициент C¢_m+1 в формуле (4) при x_m+1. Значит есть смысл увеличивать x_m+1, т.е. перейти от данного опорного решения к другому, где переменная x_m+1 ¹ 0, а вместо нее равна нулю какая-то другая. При таком переходе геометрически произойдет переход к соседней вершине многоугольника, где значение линейной функции лучше.

Однако увеличивать x_m+1 надо осторожно, так чтобы не стали отрицательными другие переменные x₁,x₂. x_m, выраженные через свободные переменные, в частности через x_m+1 формулами (3). Таким образом, должны выполняться следующие неравенства (при этом х_m+2=0, х_m+3=0,…, х_n=0, как свободные переменные):

(5) откуда

Каждое уравнение определяет оценочное отношение – границу роста переменной х_m+1, сохраняющую неотрицательность соответствующей переменной. Эта граница определяется абсолютной величиной отношения свободного члена к коэффициенту при переменной х_m+1при условии, что эти числа имеют разные знаки.

Очевидно, что сохранение неотрицательности всех переменных (допустимость решения) возможно, если не нарушается ни одна из полученных во всех уравнениях границ. Ясно, что если мы оставим остальные свободные переменные x_m+2=0. x_n=0, то x _m+1 мы можем увеличивать только до значения, равного b¢_i/ a¢_i,m+1(i=1,2,…,m), а при дальнейшем увеличении x_m+1 переменная x_j станет отрицательной.

Каждое уравнение системы ограничений определяет конечное или бесконечное наибольшее возможное значение этой переменной – оценочное отношение.

Уравнение, где достигается наибольшее возможное значение переменной, переводимой в базисные (т.е. где оценка минимальна), называется разрешающим. Его выделяем рамкой.

Встречаются различные случаи оценки роста свободной переменной, которые зависят от знаков и значений свободного члена и коэффициента при свободной переменной x_i (i=1,2,…,m). Сформулируем все возможные случаи. Обозначим: x_m+1 – переводимая свободная переменная, b’_i – свободный член, a’_im+1 – коэффициент при x_m+1. В общем виде уравнение x_i = a¢_i,m+1x_m+1 + …+a¢_i,nx_n + b¢_i определяет наибольшее возможное значение x_m+1 по следующим правилам.

Здесь, в свою очередь, могут представиться следующие случаи.

x_m+1 мы можем увеличивать только до значения, равного b¢_i/ a¢_{i m+1}, а при дальнейшем увеличении x_m+1 переменная x_j станет отрицательной.

Если во всех уравнениях (5) оценочное отношение x_m+1=µ, то max L = ¥ – задача решения не имеет.

Очевидно, что сохранение неотрицательности всех переменных (допустимость решения) возможно, если не нарушается ни одна из полученных во всех уравнениях границ. Поэтому выберем ту из переменных x₁,x₂. x_m, которая раньше всех обратится в нуль при увеличении x_m+1, т.е. ту, для которой величина b¢_i/ a¢_i,m+1 меньше всего.

Для этого найдем среди всех отношений (i=1,2,…,m) наименьшее; пусть это будет , k£m. Т. о., = min по всем i. Число a_k,m+1 называется разрешающим элементом. Обозначим указанный минимум через r= . Если он достигается сразу при нескольких значениях i, то в качестве k берем любое из них. Очевидно,r ³ 0. Ясно, что теперь x_m+1 можно увеличить до r (и не более, иначе x_i станет

Дата добавления: 2016-11-23 ; просмотров: 1142 | Нарушение авторских прав

Из приведенных основных теорем ЛП следует, что если задача ЛП имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает. По крайней мере, с одним из допустимых базисных решений системы ограничений:

· Необходимо найти все опорные решения (точки многогранника), множество которых является конечным;

· Вычислить для каждого из опорных решений значения целевой функции

· Сравнить значения целевой функции в каждой из опорных решений и выбрать оптимальное (максимальное или минимальное)

Теоретически данная схема приведет к нахождению оптимального решения, но практически её осуществление связано с большими вычислительными трудностями. Даже в задаче с двумя переменными число опорных решений может оказаться очень большим, а при большом значении n оно может достигать огромных чисел и практическое осуществление указанного перебора всех опорных решений станет невозможным. Эти вычисленные трудности возникают в результате того, что рассмотренная принципиальная схема связана с простым перебором опорных решений, т.е. в этой схеме не принимается во внимание тот факт, на сколько новое испытуемое опорное решение улучшает значение решения целевой функции и приближает нас к оптимальному решению. Если же указанный перебор опорных решений производить направлении., т.е. на каждом из шагов улучшая ( или, по крайней мере, не ухудшая) значения целевой функции то число перебираемых опорных решений можно резко сократить, что в конечном итоге приводит к весьма существенному сокращению числа шагов при отыскивании оптимума целевой функции. При использовании такой схемы, в отличие от первой, каждое последующее опорное решение выбирается таким образом, чтобы оно было лучше, (или по крайней мере, не хуже) предыдущего. Именно на каждом из шагов значение целевой функции улучшается ( или, по крайней мере, не ухудшается).

Сравним результаты применения схем простого и направленного перебора на конкретном примере.

Рассмотрим случай, когда область допустимых решений задачи ЛП (рис.1) представлена замкнутым выпуклым многоугольником ABCDEGH. Предположим, что первым из базисных решений которое найдено, является вектор ,компоненты которого соответствуют координатам угловой точки А рассматриваемого многоугольника. При использовании схемы прямого перебора решений, мы, последовательно переходя от вершины к вершине ( начиная от вершины А и заканчивая вершиной Н), вынуждены бы были испытать все семь вершин многоугольника. Предположим, что применение данного способа позволило нам определить. Что оптимум достигается в точке С.

Из чертежа видно, что, применяя метод направленного перебора, мы от вершины А перешли бы к вершине В, а затем к оптимальной вершине С, перебрав таким образом всего 3 точки, (вместо 7. Которые мы должны были бы испытать, используя метод простого перебора).

В то же время очевидно, что для практического применения метода направленного перебора необходимо знать:

· Алгоритм определения какого-либо первоначального допустимого решения задачи

· Алгоритм перехода к лучшему ( или, точнее, не к худшему) решению

· Признак, указывающий на , то, что найденое решение относительно.

Фундаментом универсального метода решения задач ЛП. Который называется симплекс-методом, является метод направленного перебора.

Геометрическая интерпретация симплекс-метода состоит в последовательном переходе от одной вершины многогранника к другой ( от первоначально выбранной вершины к одной из соседних вершин, а именно к той, у которой линейная функция принимает лучшее или, по крайней мере, не худшее значение). Этот процесс происходит до тех пор, пока не будет найдено оптимальное решение-вершина, где достигается оптимальное оптимальное решение-вершина, где достигается оптимальное значение функции (если задача имеет конечный оптимум).

Идея симплекс-метода разработана русским учёным Л.В. Канторовичем в 1939 году. На основе этой идеи американский учёный Д.Данциг в 1949 году разработал симплекс-метод, позволяющий решать любую задачу ЛП.

В настоящее время на основе этого метода разработан пакет программ с применением которого решается задачи ЛП.

Рис. 1.Геометрическая интерпретация симплекс-метода.

19. Метод Гомори. Целочисленное решение(НЕУВЕРЕНА. ))

Значительная часть задач коммерческой деятельности требует целочисленного решения. К ним относятся задачи, у которых переменные величины означают количество единиц неделимой продукции, например распределение товаров между коммерческими предприятиями, раскрой материалов, число станков при загрузке оборудования, распределение транспортных средств по рейсам, распределение коммерческих заказов между оптовыми предприятиями, продажа автомобилей, распределение самолетов по авиалиниям, количество вычислительных машин в управляющем комплексе и др. Линейные задачи, решение которых должно быть получено в целых числах, называют задачами целочисленного программирования. Задача целочисленного программирования формулируется так же, как и задача линейного программирования, но включает дополнительное требование, состоящее в том, что значения переменных должны быть целыми неотрицательными числами, например, х1 = 30 станков, х2 = 16 самолетов, х3= 7 человек. Методы целочисленной оптимизации можно разделить на три основные группы: а) методы отсечения; б) комбинированные методы; в) приближенные методы. Рассмотрим один из методов отсечения — метод Гомори. Сущность методов отсечения состоит в том, что сначала задача решается без условия целочисленности. Если полученный план целочисленный, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами: а) оно должно быть линейным; б) должно отсекать найденный оптимальный нецелочисленный план; в) не должно отсекать ни одного целочисленного плана. Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением. Алгоритм Гомори, основанный на симплексном методе, имеет простой способ построения правильного отсечения и содержит следующие этапы. 1. Задача линейного программирования решается без учета условия целочисленности симплексным или двойственным симплексным методом. Если все элементы оптимального плана целые числа, то решение заканчивается для задачи целочисленного программирования. 2. Если среди элементов оптимального решения есть нецелые числа, то необходимо выбрать элемент с наибольшей дробной частью и составить дополнительное ограничение (сечение), которое отсекает нецелочисленные решения. Дополнительное ограничение дается в том случае, если значение базисной переменной в оптимальном плане xi=bi — дробное число. Тогда некоторые элементы аij в i-й строке симплексной таблицы также дробные числа. Обозначим [bi] и [аij] целые части чисел bi и аij, т.е. наибольшие целые числа, не превышающие bi и aij. Величины дробных частей qi и qij определяются как разности следующим образом: qi = bi – [bi]; qij =аij – [aij] и являются положительными числами. Тогда неравенство qi-qi1 x1 – qi2x2 – . – qimxn £ 0, сформированное по i-й строке симплексной таблицы обладает всеми свойствами правильного отсечения. Неравенство преобразуется в уравнение путем введения дополнительной неотрицательной переменной и включается в оптимальную симплексную таблицу. 4. Полученная расширенная задача решается двойным симплексным методом. Если новый оптимальный план будет целочисленным, то задача решена. В противном случае необходимо вернуться к п. 2 алгоритма. Если в процессе решения в симплексной таблице появится уравнение с нецелым свободным членом bi и целыми коэффициентами aij, то данная задача не имеет целочисленного оптимального решения. Пример. Маркетинговые исследования указали на необходимость освоения выпуска новой продукции. Поэтому на предприятии решено установить новое технологическое оборудование на освободившейся площади 10 м2. На приобретение оборудования двух видов выделено 6 млн. руб. Комплект первого вида оборудования стоимостью 1 млн руб. устанавливается на площади 5 м2 и позволяет увеличить доход предприятия на 8 млн руб. Комплект второго вида оборудования занимает площадь 2 м2, стоит 1 млн руб. и обеспечивает увеличение дохода предприятия на 5 млн руб. Определите, какое количество технологического оборудования каждого вида следует закупить, чтобы обеспечить максимальное увеличение дохода предприятия от продажи выпускаемой продукции.

20. Двойственная задача линейного программирования и ее математическая модель.(не до конца. )

С каждой задачей ЛП связана другая задача. Название двойственной по отношению к исходной, заметим, что часто говорят о взаимодвойственных задачах т.к. если для исходной построена двойственная, а затем для неё так же построена двойственная, то получится исходная задача.

Рассмотрим пары взаимодвойственных задач позволяет решать ряд проблем:

1) Выбрать наиболее простой способ решения одной задачи, а из него найти решение другой задачи.

2) Рассматривая экономическую интерпретацию двойственных задач можно дать трактовку не только основным и дополнительным переменным, а ещё получить ряд дополнительных соотношений для прогноза и планирования, п и измененных условиях.

21. Виды двойственных задач. Правила составления симметричных двойственных задач линейного программирования.

Можно рассмотреть 2 вида двойственных задач:

Для симметричных двойственных задач характерно задание системы ограничений в виде системы неравенств.

Пусть прямая задача имеет вид:

F(x) = C₁x₁+C₂X₂+…+C_nX_n → max (в матрице после вертикальной границы вертикально стоят y1,y2,…,ym)

……………………………

Правило составления симметричной двойственной задачи ЛП.

1. каждому неравенству системы ограничений прямой задачи соответствует 1 переменная двойственной задачи Y=(y₁, y₂, …, y_m) – вектор переменных двойственной задачи. Если в прямой задаче система ограничений содержит m строк, то в двойственной задаче будет m переменных.

2. коэффициенты системы ограничений двойственной задачи получаются путем транспонирования матрицы коэффициентов прямой задачи (здесь между 2 и 3 строчкой строка точек)

3. столбец свободных членов двойственной задачи состоит из коэффициентов целевой функции прямой задачи С1, С2, …, Сn.

4. коэффициентами целевой функции двойственной задачи служат элементы столбца свободных членов прямой задачи b1, b2, …,bm

5. знаки неравенств в системе ограничений двойственной задачи противоположны знакам неравенств прямой задачи (сохраняя при этом строгость)

6. экстремумы взаимодвойственных задач противоположны, т.е. если прямая задача на max, то двойственная на min. И наоборот.

7. для симметричных задач все переменные и прямой и двойственной задачи неотрицательны.

Таким образом, с учетом правил, симметричная двойственная задача примет вид

22. Виды двойственных задач. Правила составления несимметричных двойственных задач линейного программирования.

Можно рассмотреть 2 вида двойственных задач:

В несимметричном случае одна из задач представлена в канонической форме. (в матрице после вертикальной границы вертикально стоят y1,y2,…,ym)

……………………………

. Основные правила составления двойственной задачи те же, что и в симметричном случае. Отличаются пункты 5 и 7.

5. Если в целевой функции двойственной задачи требуется найти max, то в системе ограничений будут содержаться неравенства вида ≤. А если двойственная задача на min, то ≥.

7. т.к. в прямой задаче в системе ограничений содержатся только уравнения, то в двойственной задаче условия неотрицательности отсутствуют. Т.е. yi – произвольно изменяющаяся переменная.

Таким образом для указанной прямой задачи двойственная задача примет вид:

23. Основное неравенство теории двойственности. Достаточный признак оптимальности. Первая теорема двойственности.

Основное неравенство теории двойственности: для любых допустимых решений пары взаимодвойственных задач X(x1, x2,…,xn), Y(y1,y2,…,ym) справедливо неравенство F(X)≤Z(Y)

Достаточный признак оптимальности:

если X*=(x*1,x*2,…,x*n) и Y*=(y*1,y*2,…,y*m) – допустимые решения задач, для которых выполняется условие F(X*)=Z(Y*), то X* и Y* – оптимальные решения двойственных задач!

Первая основная теорема двойственности:

если одна из взаимодвойственных задач имеет оптимальное решение, то другая задача также имеет оптимальное решение, причем для любых оптимальных решений X* и Y* выполняется равенство F(X*)=Z(Y*). Обратное утверждение тоже справедливо. Однако, если одна из двойственных задач не имеет решения вследствие ограниченности целевой функции F(X)→∞, то другая задача не будет иметь решения вследствие несовместности системы ограничений. Обратное утверждение не всегда верно, т.е. если задача имеет несовместную систему ограничений, то двойственная к ней может быть как неограниченной, так и ограниченной.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: