Задача о ранце метод ветвей и границ

При написании вариантов решения алгоритма задачи о рюкзаке, написал все самые знаменитые варианты решения: полный перебор, жадный, используя динамическое программирование. А вот с вариант используя метод ветвей и границ, никак не получается. Нашел такой псевдокод :

1. Разбиваем текущую задачу на подзадачи.
2. Для каждой подзадачи выполняем оценку минимального и максимального значения нашей функции. 2.1. Если оценка снизу лучше текущего рекорда, то она становится новым рекордом. 2.2. Если оценка сверху хуже текущего рекорда, то отбрасываем эту подзадачу.
3. Выбираем из нерешённых подзадач самую перспективную. 3.1. Если нерешённых подзадач не осталось, то рекорд – это решение. (goto 5)
4. Решаем выбранную подзадачу (goto 1)
5. Ура!

Будьте добры помогите с наброском кода и объясните псевдокод.

1 ответ 1

Основой любого алгоритма, построенного по стратегии Ветвей и Границ является древовидный полный перебор. То есть "скелетом" данной стратегии является банальный рекурсивный просмотр всех возможных вариантов наполнения рюкзака. На каждом уровне рекурсии одна рекурсивная подветка соответствует варианту "берем следующий предмет" (если позволяет остаточная емкость рюкзака), вторая рекурсивная подветка соответствует варианту "не берем следующий предмет". Это и есть наши подзадачи. Это и есть Ветви.

Каждая листовая вершина нашего дерева перебора будет соответствовать какому-то варианту наполнения рюкзака и все такие варианты будут перебраны данной стратегией. Если реализовать все это буквально, то мы, перебрав и сравнив все возможные варианты, найдем точное решение нашей задачи. В каком порядке просматриваются предметы значения не имеет, так как в конечном итоге мы все равно переберем все возможные варианты.

Например, вот так может выглядеть решение (С++), выполненное через полный перебор

(Все это можно сделать и компактнее, но я заранее закладываю задел на будущие модификации под метод Ветвей и Границ.)

На таком входе, как видите, полный перебор выполнит рассмотрение 57 вариантов.

Идея Границ в стратегии Ветвей и Границ сводится к тому, что мы должны уметь относительно недорого заранее предсказывать наиболее оптимистичный вариант решения для каждой рекурсивной подветви, не проводя полного анализа этой подветви. Если этот наиболее оптимистичный вариант заведомо хуже уже имеющихся у нас на данный момент вариантов решения, то тратить усилия на просмотр такой подветки нет никакого смысла.

В данном случае (задача на максимизацию) требуется, чтобы это предсказание давало нам приблизительную оценку сверху для наилучшего потенциального решения, которое можно извлечь из рекурсивной подветви. Чем точнее будет эта оценка сверху, тем лучше (но надо найти оптимальный баланс между точностью оценки и трудоемкостью ее получения). Главное только, чтобы это была именно оценка сверху, т.е. она должна быть заведомо не меньше наилучшего решения для данной рекурсивной ветви.

Если у нас есть достаточно быстрый и дешевый способ построения такой оценки, мы будем использовать его для отсечения бесперспективных ветвей в переборе. Действуя по обычной переборной стратегии, в каждый момент времени мы имеем текущее лучшее решение, называемое рекордным решением. В процессе поиска других решений, спускаясь по нашему дереву перебора, мы будем использовать выбранный метод оценки сверху для оценки потенциального решения в очередной рекурсивной подветви. Если эта оценка говорит нам, что побить нынешний рекорд в данной подветви у нас нет никаких шансов, то продолжать просмотр данной рекурсивной ветви нет никакого смысла.

В классическом методе Ветвей и Границ для решения задачи максимизации оценка снизу не нужна. Нужна только оценка сверху. Однако если у вас есть возможность без лишних усилий получить еще и оценку снизу, то ее действительно можно применять для раннего задания значения рекорда (еще до построения первых завершенных решений), тем самым повышая шансы на то, что оценка сверху позволит нам отсеивать бесперспективные ветки на более ранней стадии. Но, еще раз, оценка снизу в задаче максимизации – не обязательна.

Для дискретной задачи о рюкзаке традиционным способом вычисления оценки сверху является "жадный" алгоритм для решения дробной задачи о рюкзаке (под "дробной задачей" имеется я виду возможность брать предметы лишь частично). Такая задача решается тривиально: в рюкзак надо класть предметы в порядке убывания их стоимости на единицу веса. Последний предмет, возможно, поместится в рюкзак лишь частично. Стоимость такого "жадно" заполненного рюкзака – это и есть оценка сверху для решения исходной дискретной задачи.

Вот тот же самый код, на том же самом входе, но теперь с реализацией метода Ветвей и Границ

В этом варианте кода я заранее сортирую входной набор предметов в порядке убывания их стоимости на единицу веса. Это позволяет тривиальным образом реализовать функцию вычисления оценки сверху find_best_greedily . Это также, возможно, накладывает свой (положительный) отпечаток на порядок формирования решений в процессе перебора, т.е. мы стараемся как можно раньше положить в наш рюкзак наиболее эффективные заполнители.

Как видите, этот вариант проверяет только 16 листовых вариантов, а в остальных случаях поддеревья рекурсивных вызовов "отвергаются" на ранних стадиях как бесперспективные на основе вычисленной предварительной оценки сверху.

Вышеприведенного уже достаточно для того, чтобы получить алгоритм по стратегии Ветвей и Границ. Дополнительной модификацией данной стратегии является приоритизация рекурсивных подветвей на основе вычисленной оценки сверху, т.е. обработка в процессе рекурсивного перебора в первую очередь именно той подветви, которая дает более высокую оценку и, поэтому, выглядит более перспективной. Такая подветвь имеет лучшие шансы улучшить наш рекорд как можно раньше и тем самым дать нам возможность раньше отказаться от обработки второй подветви перебора.

В том же примере кода прямая модификация функции find_best для реализации этой стратегии может выглядеть так

В этом варианте проверяется только 2 листовых варианта, т.е. бесперспективные поддеревья рекурсивных вызовов "отвергаются" на еще более ранних стадиях.

В пункте 2 я несколько схитрил, так как в процессе рекурсивного просмотра сначала проверяю вариант "не брать очередной предмет", а затем вариант "брать очередной предмет". Интуитивно кажется, что разумнее было бы сначала проверять вариант "брать очередной предмет", т.к. мы стараемся именно максимизировать наполнение рюкзака. Это должно дать нам возможность раньше находить качественные рекордные решения и тем самым усиливать отсев бесперспективных ветвей перебора. Действительно, если в варианте 2 поменять местами рекурсивные ветки, то реализация найдет оптимальное решение, просмотрев всего 2 листовых варианта, т.е. не больше чем в варианте 3. То есть на этом примере приоритизация ветвей из варианта 3 ничего на самом деле не дает. Наверное существуют входы, на которых приоритизация из шага 3 должна давать положительный эффект, но возможно что эта овчинка и не стоит выделки.

Также, в примерах выше я взял слишком большой размер рюкзака – 1500, что приводит к тому, что в рюкзак помещается "почти все". Возможно, более интересное поведение алгоритма получится наблюдать на рюкзаках меньшего размера. 900 выглядит интересно.

Примечание: метод ветвей и границ используется также и в задаче коммивояжера.

Пример №1 . В задаче методом Гомори (или методом ветвей и границ) найти оптимальные решения задач целочисленного линейного программирования. Дать геометрическую интерпретацию процесса решений задач.
Z=3x₁ + 2x₂ → max
при ограничениях:
x₁ + x₂ ≤ 13
x₁ – x₂ ≤ 6
-3x₁ + x₂ ≤ 9
x₁≥0, x₂ ≥0
x₁, x₂ – целые числа.

Пример №2 .
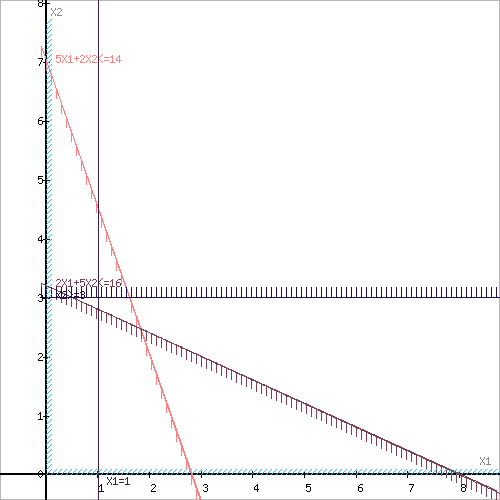
5x₁ + 2x₂ ≤ 14
2x₁ + 5x₂ ≤ 16
x₁ , x₂ – целые числа
Z = 3x₁ + 5x₂ → max
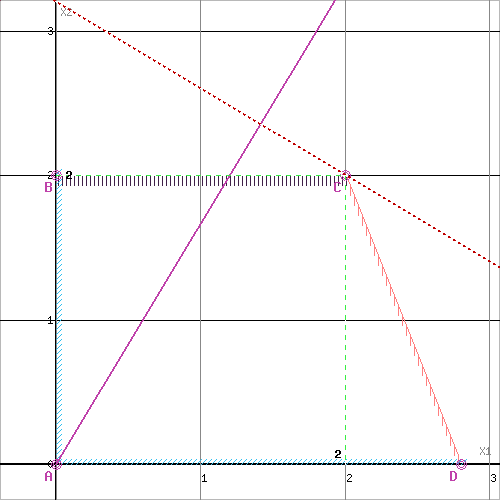
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

Область допустимых решений представляет собой треугольник.
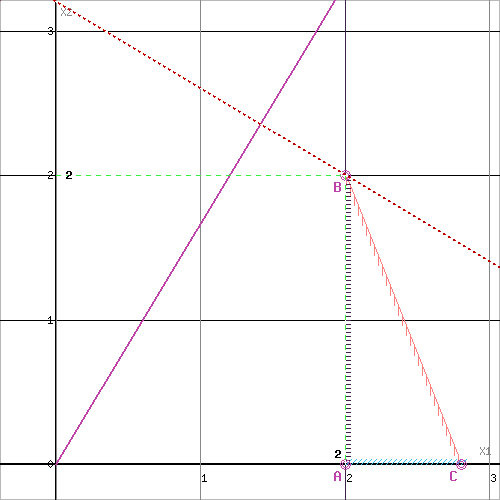
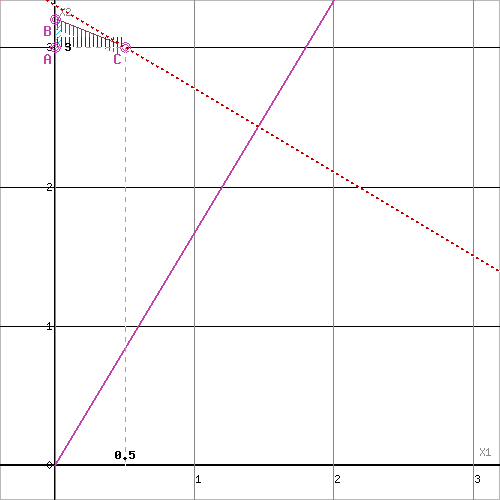
Прямая F(x) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
5x₁+2x₂≤14
x₁≥2

Решив систему уравнений, получим: x₁ = 2, x₂ = 2
Откуда найдем максимальное значение целевой функции:
F(X) = 3*2 + 5*2 = 16

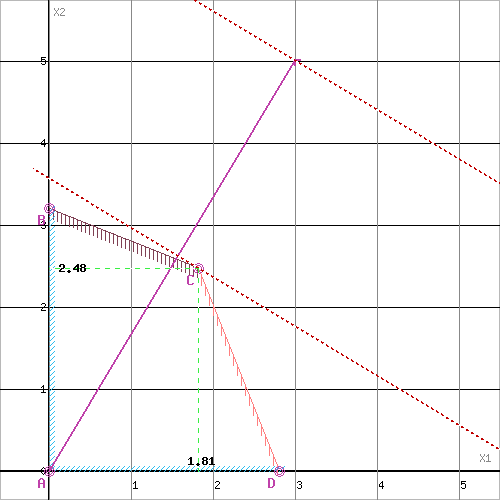
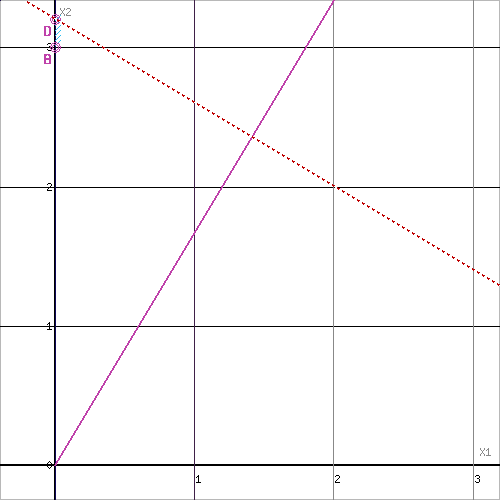
Область допустимых решений представляет собой многоугольник
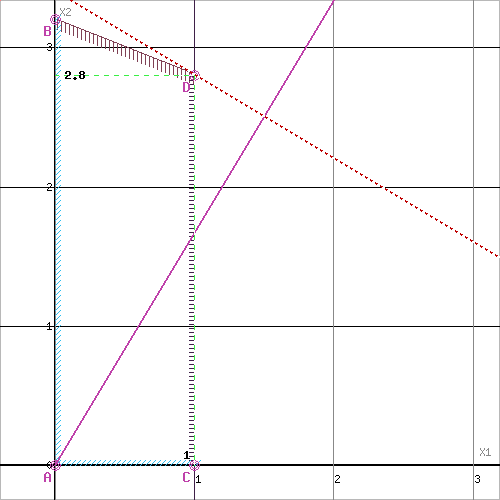
Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (2) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
2x₁+5x₂≤16
x₁≤1

Решив систему уравнений, получим: x₁ = 1, x₂ = 2.8
Откуда найдем максимальное значение целевой функции:
F(X) = 3*1 + 5*2.8 = 17

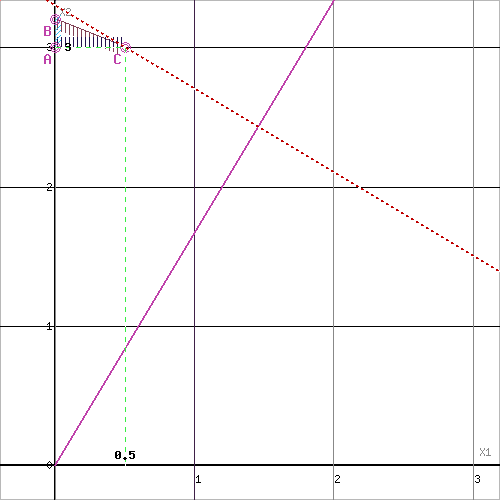
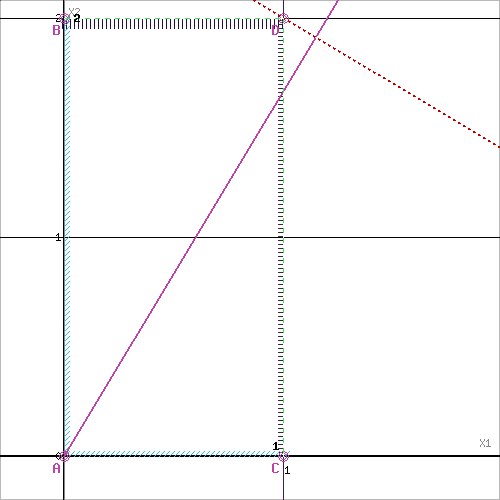
Решим графически задачу 111 как задачу ЛП.
5x₁+2x₂≤14 (1)
2x₁+5x₂≤16 (2)
x₂≥3 (3)
x₁≥1 (4)
x₁≥0 (5)
x₂≥0 (6) Задача не имеет допустимых решений. ОДР представляет собой пустое множество

На этой задаче показано, как конкретно применяется к ее решению метод ветвей и границ и динамического программирования.

Задача формулируется следующим образом. Перед походом в рюкзак вместимостью не более А единиц веса из набора I – <1, 2, п) предметов, каждый весом я, и «ценностью» с,-,

необходимо положить те предметы, которые максимизируют суммарную «ценность» груза и по весу помещаются в рюкзак. Непосредственно термин «рюкзак» толкуется достаточно широко. Это может быть и собственно рюкзак, и контейнер, и подводная лодка, и самолет-бомбардировщик с отсеком для бомб и т. д. Поэтому к разработке эффективных алгоритмов решения этой задачи в свое время было приложено немало усилий.

Математическую формулировку задачи получим следующим образом. Введем в рассмотрение переменные х,, /’=1,2. //такие, что х,- =1, если /’-й предмет кладется в рюкзак, и х₁ = 0, в противном случае. Тогда выражение IV = с,х, +с₂х₂+. + с,х,+. + с_пх_п =

= ^с,Ху будет определять суммарную «ценность» груза при соот-/=1

Требуется найти такой набор переменных х_/? /е /, который доставляет

• (6.2)
• (6.3)
• 5>х, ^ V, /=1

1, если /’-й предмет помещен в рюкзак, 0, в противном случае.

Решение задачи о рюкзаке в такой формулировке определено на множестве комбинаций, состоящих из последовательностей нулей и единиц длиной п. Например, при /7 = 3 это комбинации 000, 001,010, 100, 011,110, 101, 111. Согласно закону комбинаторики всего таких комбинаций будет 2/7. Если же отбросить совсем неподходящие комбинации 000, 111, которые указывают на то, что в рюкзак либо не кладется ни один предмет, либо помещаются все предметы, то их число будет равным 2" – 2. Кроме этого число комбинаций 2" -2 будет ограничено величиной V, определяющей допустимый груз рюкзака. Таким образом, решение задачи следует искать на некотором подмножестве комбинаций, число элементов которого меньше 2" -2. Безусловно, лучшую комбинацию можно найти методом прямого их перебора, если число п невелико. По возможностям современных персональных компьютеров такой поиск сравнительно быстро может быть осуществлен, если п не больше 30. В этом случае придется сгенерировать 2 30 – 2 комбинаций, проверить условие (2) и подсчитать значение IV не более 2 30 -2 раз, что составит 2 10 -2 10 -2 10 -2 = 1024-1024-1024-2 = 1 073 741 822 указанных действий.

По элементам множества — комбинациям из нулей и единиц, на которых определена оптимизируемая функция, задача о рюкзаке сходна с задачей о выполнимости булевой формулы, о которой говорилось выше. Поскольку эта задача ЛФ-полная, можно предполагать, что и задача о рюкзаке также принадлежит к этому классу задач. Это действительно так, и строгое доказательство этого факта изложено в [26].

Таким образом, задача о рюкзаке точно может быть решена только алгоритмами с экспоненциальным временем счета. Вначале рассмотрим, как можно применить и построить алгоритм решения этой задачи по схеме ветвей и границ.

При изложении этого метода (п. 6.1) говорилось о том, что он предполагает выбор и разработку трех процедур: принципа разбиения исходного множества решений задачи на подмножества (выработку схемы ветвления), определения стратегии ветвления, т. е. правила выбора очередного подмножества для разбиения, формулировку оценочной задачи, решения которой определяют нижние (верхние) границы оптимизируемой функции на подмножествах разбиения.

Применительно к рассматриваемой задаче о рюкзаке разбиение исходного множества комбинаций и всех последующих подмножеств будем осуществлять на два подмножества. Первое из них содержит такие комбинации, для которых очередное х,- = 0, а второе — такие, что очередное х,- = 1.

Стратегию ветвления примем такой, что для очередного разбиения выбирается то подмножество решений, для которого максимальна верхняя граница оптимизируемой функции. Тогда полученное первоначальное дерево поиска, например, для п – 4 может быть таким, как на рис. 6.4.

Для формулировки оценочной задачи проведем следующие рассуждения. Предположим, выбрана некоторая комбинация х,, х₂, х₃, . х_к, для нее найдена сумма весов а_х, а₂, а₃, . а_к, меньшая V, а выбор любого х_к+1 = 1 из оставшегося их набора превышает допустимый вес рюкзака, т. е. я, + а₂ + а₃+. + а_к + +. + а_к+1 > V. Тогда, чтобы выполнялось требование а₁+а₂ + + а₃+. + а_к+. + а_к+, = V необходимо дать возможность переменной х_А+1 изменяться в пределах 0 с к х к+1, т – е – является по отношению к ней верхней границей. Таким образом, оценочная задача, служащая для вычисления верхних границ оптимизируемой функции на подмножествах, формулируется так: найти

Рис. 6.4. Первоначальное дерево ветвления в задаче о рюкзаке