Содержание
Задачи коммивояжера решаются посредством различных методов, выведенных в результате теоретических исследований. Все эффективные методы (сокращающие полный перебор) — методы эвристические. В большинстве эвристических методов находится не самый эффективный маршрут, а приближённое решение. Зачастую востребованы алгоритмы постепенно улучшающие некоторое текущее приближенное решение. Выделяют следующие группы методов решения задач коммивояжера, которые относят к простейшим:
Полный перебор (или метод «грубой силы») — метод решения задачи путем перебора всех возможных вариантов. Сложность полного перебора зависит от количества всех возможных решений задачи. Если пространство решений очень велико, то полный перебор может не дать результатов в течение нескольких лет или даже столетий.
Обычно выбор решения можно представить последовательностью выборов. Если делать эти выборы с помощью какого-либо случайного механизма, то решение находится очень быстро, так что можно находить решение многократно и запоминать «рекорд», т. е. наилучшее из встретившихся решений. Этот наивный подход существенно улучшается, когда удается учесть в случайном механизме перспективность тех или иных выборов, т. е. комбинировать случайный поиск с эвристическим методом и методом локального поиска. Такие методы применяются, например, при составлении расписаний для Аэрофлота.
· Жадные алгоритмы (метод ближайшего соседа, метод включения ближайшего города, метод самого дешевого включения);
Жадный алгоритм – алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами. «Жадным» этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность. При решении задачи коммивояжера жадный алгоритм превратится в стратегию «иди в ближайший (в который еще не входил) город». Жадный алгоритм, очевидно, бессилен в этой задаче. Рассмотрим для примера сеть (рис. 2), представляющую узкий ромб. Коммивояжер стартует из города 1. Алгоритм «иди в ближайший город» выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.
· Метод минимального остовного дерева (деревянный алгоритм);
В основе алгоритма лежит утверждение: «Если справедливо неравенство треугольника, то для каждой цепи верно, что расстояние от начала до конца цепи меньше (или равно) суммарной длины всех ребер цепи». Это обобщение расхожего убеждения, что прямая короче кривой. Деревянный алгоритм для решения задачи коммивояжера будет следующим: строится на входной сети задачи коммивояжера кратчайшее остовное дерево и удваиваются все его ребра. В результате получаем граф — связный с вершинами, имеющими только четные степени. Затем строится эйлеров цикл, начиная с вершины 1, цикл задается перечнем вершин. Просматривается перечень вершин, начиная с 1, и зачеркивается каждая вершина, которая повторяет уже встреченную в последовательности. Останется тур, который и является результатом алгоритма.
Доказано, что деревянный алгоритм ошибается менее чем в два раза, поэтому такие алгоритмы называют приблизительными, а не просто эвристическими.
· Метод имитации отжига.
Экзотическое название данного алгоритма связано с методами имитационного моделирования в статистической физике, основанными на технике Монте-Карло. Исследование кристаллической решетки и поведения атомов при медленном остывании тела привело к появлению на свет вероятностных алгоритмов, которые оказались чрезвычайно эффективными в комбинаторной оптимизации. Впервые это было замечено в 1983 году. Сегодня этот алгоритм является популярным как среди практиков благодаря своей простоте, гибкости и эффективности, так и среди теоретиков, поскольку для данного алгоритма удается аналитически исследовать его свойства и доказать асимптотическую сходимость. Алгоритм имитации отжига относится к классу пороговых алгоритмов локального поиска. На каждом шаге этого алгоритма для текущего решения ik в его окрестности N(ik) выбирается некоторое решение j и, если разность по целевой функции между новым и текущим решением не превосходит заданного порога tk, то новое решение j заменяет текущее. В противном случае выбирается новое соседнее решение. На практике применяются различные модификации более эффективных методов:
· Метод ветвей и границ;
Метод ветвей и границ предложен в 1963 году группой авторов Дж. Литлом, К. Мурти, Д. Суини, К. Кэролом. Широко используемый вариант поиска с возвращением, фактически является лишь специальным частным случаем метода поиска с ограничениями 4 . Ограничения в данном случае основываются на предположении, что на множестве возможных и частичных решений задана некоторая функция цены и что нужно найти оптимальное решение, т.е. решение с наименьшей ценой. Для применения метода ветвей и границ функция цены должна обладать тем свойством, что цена любого частичного решения не превышает цены любого расширения этого частичного решения (Заметим, что в большинстве случаев функция цены неотрицательна и даже удовлетворяет более сильному требованию). Столь большой успех применения данного метода объясняется тем, что авторы первыми обратили внимание на широту возможностей метода, отметили важность использования специфики задачи и сами воспользовались спецификой задачи коммивояжера.
В основе метода ветвей и границ лежит идея последовательного разбиения множества допустимых решений на подмножества. На каждом шаге метода элементы разбиения подвергаются проверке для выяснения, содержит данное подмножество оптимальное решение или нет. Проверка осуществляется посредством вычисления оценки снизу для целевой функции на данном подмножестве. Если оценка снизу не меньше рекорда — наилучшего из найденных решений, то подмножество может быть отброшено. Проверяемое подмножество может быть отброшено еще и в том случае, когда в нем удается найти наилучшее решение. Если значение целевой функции на найденном решении меньше рекорда, то происходит смена рекорда. По окончанию работы алгоритма рекорд является результатом его работы. Если удается отбросить все элементы разбиения, то рекорд — оптимальное решение задачи. В противном случае, из неотброшенных подмножеств выбирается наиболее перспективное (например, с наименьшим значением нижней оценки), и оно подвергается разбиению. Новые подмножества вновь подвергаются проверке и т.д.
· Метод генетических алгоритмов;
«Отцом-основателем» генетических алгоритмов считается Джон Холланд, книга которого «Адаптация в естественных и искусственных системах» (1975) является основополагающим трудом в этой области исследований. Генетический алгоритм — это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений. Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе. Генетические алгоритмы служат, главным образом, для поиска решений в многомерных пространствах поиска.
· алгоритм муравьиной колонии.
Алгоритмы муравья, или оптимизация по принципу муравьиной колонии (название было придумано изобретателем алгоритма, Марко Дориго), основаны на применении нескольких агентов и обладают специфическими свойствами, присущими муравьям, и используют их для ориентации в физическом пространстве. Алгоритмы муравья особенно интересны потому, что их можно использовать для решения не только статичных, но и динамических проблем, например, в изменяющихся сетях.
2.4 Метод ветвей и границ
Для решения задачи коммивояжера методом ветвей и границ необходимо выполнить следующую последовательность действий:
(1) Построение матрицы с исходными данными.
(2) Нахождение минимума по строкам.
(3) Редукция строк.
(4) Нахождение минимума по столбцам.
(5) Редукция столбцов.
(6) Вычисление оценок нулевых клеток.
(7) Редукция матрицы.
(8) Если полный путь еще не найден, переходим к пункту 2, если найден к пункту 9.
(9) Вычисление итоговой длины пути и построение маршрута.
Подробная методика решения
В целях лучшего понимания задачи будем оперировать не понятиями графа, его вершин и т.д., а понятиями простыми и максимально приближенными к реальности: вершины графа будут называться «города», ребра их соединяющие – «дороги».
Итак, методика решения задачи коммивояжера:
1. Построение матрицы с исходными данными
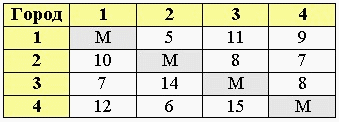
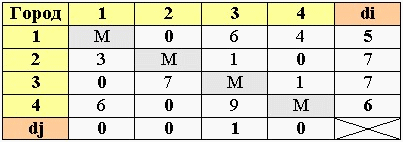
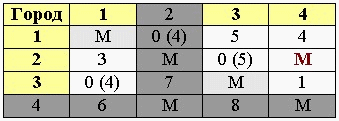
Сначала необходимо длины дорог соединяющих города представить в виде следующей таблицы:
В нашем примере у нас 4 города и в таблице указано расстояние от каждого города к 3-м другим, в зависимости от направления движения (т.к. некоторые ж/д пути могут быть с односторонним движением и т.д.).
Расстояние от города к этому же городу обозначено буквой M. Также используется знак бесконечности. Это сделано для того, чтобы данный отрезок путь был условно принят за бесконечно длинный. Тогда не будет смысла выбрать движение от 1-ого города к 1-му, от 2-ого ко 2-му, и т.п. в качестве отрезка маршрута.
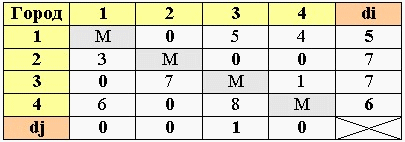
2. Нахождение минимума по строкам
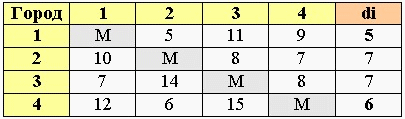
Находим минимальное значение в каждой строке (di) и выписываем его в отдельный столбец.
3. редукция строк
Производим редукцию строк – из каждого элемента в строке вычитаем соответствующее значение найденного минимума (di).
В итоге в каждой строке будет хотя бы одна нулевая клетка.
4. Нахождение минимума по столбцам
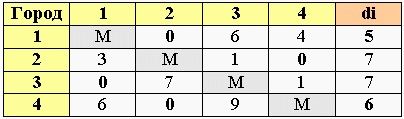
Далее находим минимальные значения в каждом столбце (dj). Эти минимумы выписываем в отдельную строку.
5. редукция столбцов
Вычитаем из каждого элемента матрицы соответствующее ему dj.
В итоге в каждом столбце будет хотя бы одна нулевая клетка.
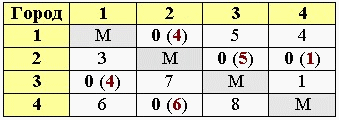
6. Вычисление оценок нулевых клеток
Для каждой нулевой клетки получившейся преобразованной матрицы находим «оценку». Ею будет сумма минимального элемента по строке и минимального элемента по столбцу, в которых размещена данная нулевая клетка. Сама она при этом не учитывается. Найденные ранее di и dj не учитываются. Полученную оценку записываем рядом с нулем, в скобках.
И так по всем нулевым клеткам:
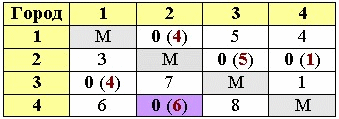
7. редукция матрицы
Выбираем нулевую клетку с наибольшей оценкой. Заменяем ее на «М». Мы нашли один из отрезков пути. Выписываем его (от какого города к какому движемся, в нашем примере от 4-ого к 2-му).
Ту строку и тот столбец, где образовалось две «М» полностью вычеркиваем. В клетку соответствующую обратному пути ставим еще одну букву «М» (т.к. мы уже не будем возвращаться обратно).
8. если полный путь еще не найден, переходим к пункту 2, если найден к пункту 9
Если мы еще не нашли все отрезки пути, то возвращаемся ко 2-му пункту и вновь ищем минимумы по строкам и столбцам, проводим их редукцию, считаем оценки нулевых клеток и т.д.
Если все отрезки пути найдены (или найдены еще не все отрезков, но оставшаяся часть пути очевидна) – переходим к пункту 9.
9. вычисление итоговой длины пути и построение маршрута
Найдя все отрезки пути, остается только соединить их между собой и рассчитать общую длину пути (стоимость поездки по этому маршруту, затраченное время и т.д.). Длины дорог соединяющих города берем из самой первой таблицы с исходными данными.
В нашем примере маршрут получился следующий: 4 → 2 → 3 → 1 → 4.
Общая длина пути: L = 30.
В данной работе мы познакомились с основными понятиями теории графов, дали представление о задаче коммивояжера, описали основные методы оптимизации метод. Также привели пример использования метода ветвей и границ для решения задачи коммивояжера.
Еще раз отметим, что задача коммивояжера является одной из самых важнейших задач в теории графов. Возможность представления различных производственных процессов на языке теории графов и умение решить сформулированную математическую задачу позволяют найти оптимальную стратегию ведения хозяйства, сэкономить ресурсы, выполнить поставленную задачу в более короткие сроки.
Список использованной литературы
1. Кирсанов М.Н. «Графы в Maple», М. Физматлит, 2007.
2. Зыков А.А. «Основы теории графов» , М. «Вузовская книга», 2014
3. Уилсон Р. «Введение в теорию графов» , М. «Мир», 2010
4. Берж К. "Теория графов и ее применение", М., ИЛ, 2008;
5. Гарднер М. "Математические досуги", М. "Мир", 2009(глава 35);
6. "В помощь учителю математики", Йошкар-Ола, 2011 (ст. "Изучение элементов теории графов");
7. Олехник С.Н., Нестеренко Ю.В., Потапов М.К. "Старинные занимательные задачи", М. "Наука", 2008;
8. Гарднер М. "Математические головоломки и развлечения", М. "Мир",2012;
9. Оре О. "Графы и их применения", М. "Мир", 2011;
10. Зыков А.А. "Теория конечных графов", Новосибирск, "Наука", 2009;
11. Реньи А., "Трилогия о математике", М., "Мир", 2010.
Введение
Этот документ продолжает тему задачи коммивояжёра. Мы обсудим различные эвристические алгоритмы, которые не гарантируют получения точного решения, однако, иногда дают кратчайший путь или близкий к нему. Первые два метода (жадный алгоритм и метод шнурка), обычно, используются для получения первого приближения к решению задачи. Затем его можно улучшить остальными эвристиками, описанными в документе.
Вообще, эффективность эвристических методов повышается при их комбинировании. Если первые два метода не зависят от "предыстории" поиска, то последовательность остальных методов важна и при удачном их сочетании результат может существенно улучшиться.
Полученный при помощи эвристик путь, в дальнейшем используется как стартовый для поиска с возвратом. При этом возможно не только его улучшение, но и доказательство оптимальности (если поиск закончит свою работу).
Жадный алгоритм
Идея этого алгоритма очень проста. При выборе очередного города берётся ближайший город в котором мы ещё не были. Такой подход, по понятным причинам называется "жадным". К сожалению, если в начале путь получается коротким, то в конце часто возникает очень большой прирост его длины.
В жадном алгоритме принципиально какой город выбирается в качестве стартового. Чтобы улучшить результат, будем по очереди делать стартовым каждый город, выбирая тот вариант, который даст кратчайший путь. В начале следующей итерации вспомогательный массив way заполняется номерами городов: way = [0,1,2,3. N-1] и на первое место ставится город j=0,1,2. N-1. Для этого он меняется местами с нулевым элементом массива. Затем ищется ближайший к нему город и ставится на первое место (снова при помощи перестановки элементов массива функцией swap). Эти действия продолжаются, пока не сформируется полный путь:
Приведём длину пути, сам путь и карту городов в конце каждого цикла по стартовому городу j для карты городов, созданной функцией create(100,100, 7, lcg, true) (картинки увеличены в scale = 2.2 раза): В этом случае города 1, 6 и 7, в качестве стартовых, привели к точному (и единственному) решению с длиной пути 305. Самым неудачным оказался бы старт с города 3, который приводит (при "простом" жадном выборе очередного горорда) к пути длиной 378.
Жадный алгоритм (с перебором стартового города) имеет кубическое время работы T
N 3 . Поэтому для большого числа городов N стоит переписать функцию greed для вызова её в таймере. Соответствующий код (функции greedInit и greedTimer) можно найти в исходниках класса salesman.js.
Метод шнурка
Метод шнурка разработан для евклидовой версии задачи коммивояжёра и основан на "человеческом" подходе к решению задачи. На первом этапе все города окружаются охватывающим полигоном, так как это сделано на картинке ниже:
Затем в таймере, в каждый сегмент полученного контура вставляется "промежуточный" город, который минимальным образом увеличивает общий путь.
Нажми на кнопку
Для охватывания точек на плоскости выпуклым полигоном, воспользуемся алгоритмом Джарвиса. Сначала найдём самую верхнюю из самых левых точек cur (верхний левый угол – ось y вниз!). Выше это город номер 18, и он, очевидно, лежит на охватывающем полигоне. Затем ищем ближайшую к cur точку nxt, такую, что вектор в остальные точки i лежит слева от вектора проходящего через nxt – cur (если смотреть из точки cur). Это проверяется знаком векторного произведения (nxt – cur) x (i – cur). Если оно равно нулю, это значит, что точки лежат на одной прямой. После этого, точку nxt (выше 59) делаем cur и повторяем вычисления, формируя охватывающий контур против часовой стрелки. Алгоритм останавливается, когда возвращается к исходной точке beg: Функция isInArray (статическая) проверяет, есть ли в массиве minWay значение i. В конце подготавливается массив was, i-й элемент которого равен true, если i-й город уже находится в пути.
Дальнейшие вычисления проводятся в таймере и они достаточно незатейливые. Выбирается сегмент [i1, i2] и город i, добавление которого между i1 и i2 увеличивает длину пути минимальным образом:
Перестановка соседей
Перейдём теперь к эвристикам которые, обычно, позволяют улучшить найденный предыдущими двумя методами путь. Простейшей из них является перестановка двух соседних городов в пути. Если такая перестановка приводит к уменьшению общей длины пути, то она запоминается. Этот приём позволяет "распутывать маленькие петли":
Перестановка соседей имеет квадратичное время работы, поэтому сделаем её "не таймерной":
Выше использована функция next получения следующего индекса, с учётом перодичности движения по массиву minWay:
Поэкспериментировать с этой эвристикой можно на страничке сравнения различных методов (метод " перевороты"). Лучше её запускать после жадного алгоритма или метода шнурка.
Перестановка пар
В этой эвристике берутся две пары соседних узлов и проверяется, уменьшится ли расстояние, если переставить местами по одному городу из каждой пары. Ниже одна пара – это узлы b1 и b2, а вторая пара – узлы e1 и e2. Пунктирными линиями обозначены остальные участки пути (с не нарисованными на них узлами) и стрелками – направление движения. Понятно, что если после города b1 пойти не в b2, а в e1, то общая длина пути уменьшится (второй рисунок). При такой замене необходимо также обратить последовательность прохождения участка пути A (см. направление стрелок):
| [B] b1b2 [A] e1e2 | [B] b1e1 [A] inv b2e2 |
Эвристика перестановки пар в классе Salesman сделана "таймерной" (функции swapInit и swapTimer). Алгоритм начинается с индексов beg1=0, beg2=1 (в массиве minWay), а для второй пары берутся соседние города с индексами end1=2 и end2=3. Затем в таймерной функции вторая пара начинает скользить вдоль пути в поисках возможных перестановок. Если они произошли, увеличивается счётчик числа перестановок cntSwaps "на круге". Если при полном обходе второй парой пути не произошло ни одной перестановки, то первая пара сдвигается на один индекс. Вторая опять становится после неё и всё повторяется.
На результат работы этой эвристики можно посмотреть на страничке сравнения методов (метод swap).
Частичный перебор
Ещё одна эвристика обобщает метод "перестановки соседей". В ней выбирается небольшой участок пути ("окно перестановок"). Ниже на рисунке приведено окно шириной в четыре города между узлами b и e (попавшие в него города обведены пунктиром). Города внутри окна переставляются всеми возможными способами. После проведения этих перестановок окно сдвигается вдоль пути на один город. Процедура повторяется до тех пор, пока при полном прохождении окна перестановок вдоль пути не будет найдено ни одного лучшего решения. Соответствующие функции moveInit и moveTimer есть в исходниках. Эту эвристика, как и остальные, можно запустить на страничке сравнения методов (метод move perm).
Задачу комивояжера можно решить используя следующие методы:
Жадный алгоритм
Жадный алгоритм – алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами. «Жадным» этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность.
Посмотрим, как поведет себя при решении ЗК жадный алгоритм. Здесь он превратится в стратегию «иди в ближайший (в который еще не входил) город». Жадный алгоритм, очевидно, бессилен в этой задаче. Рассмотрим для примера сеть на рис. 2, представляющую узкий ромб. Пусть коммивояжер стартует из города 1. Алгоритм «иди вы ближайший город» выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.
В пользу процедуры «иди в ближайший» можно сказать лишь то, что при старте из одного города она не уступит стратегии «иди в дальнейший».
Как видим, жадный алгоритм ошибается. Можно ли доказать, что он ошибается умеренно, что полученный им тур хуже минимального, положим, в 1000 раз? Мы докажем, что этого доказать нельзя, причем не только для жадного логарифма, а для алгоритмов гораздо более мощных. Но сначала нужно договориться, как оценивать погрешность неточных алгоритмов, для определенности, в задаче минимизации. Пусть fB – настоящий минимум, а fA – тот квазиминимум, который получен по алгоритму. Ясно, что fA/ fB?1, но это – тривиальное утверждение, что может быть погрешность. Чтобы оценить её, нужно зажать отношение оценкой сверху:
где, как обычно в высшей математике, е?0, но, против обычая, может быть очень большим. Величина е и будет служить мерой погрешности. Если алгоритм минимизации будет удовлетворять неравенству (5), мы будем говорить, что он имеет погрешность е.
Предположим теперь, что имеется алгоритм А решения ЗК, погрешность которого нужно оценить. Возьмем произвольный граф G (V,E) и по нему составим входную матрицу ЗК:
- 1,если ребро (i,j) принадлежит Е
- 1+nе в противном случае
Если в графе G есть гамильтонов цикл, то минимальный тур проходит по этому циклу и fB = n. Если алгоритм А тоже всегда будет находить этот путь, то по результатам алгоритма можно судить, есть ли гамильтонов цикл в произвольном графе. Однако, непереборного алгоритма, который мог бы ответить, есть ли гамильтонов цикл в произвольном графе, до сих пор никому не известно. Таким образом, наш алгоритм А должен иногда ошибаться и включать в тур хотя бы одно ребро длины 1+nе. Но тогда fA?(n-1)+(1+nе) так что fA/fB=1+nе т.е. превосходит погрешность е на заданную неравенством (5). О величине е в нашем рассуждении мы не договаривались, так что е может быть произвольно велик.
Таким образом доказана следующая теорема.
Либо алгоритм А определяет, существует ли в произвольном графе гамильтонов цикл, либо погрешность А при решении ЗК может быть произвольно велика.
Это соображение было впервые опубликовано Сани и Гонзалесом в 1980 г. Теорема Сани-Гонзалеса основана на том, что нет никаких ограничений на длину ребер. Теорема не проходит, если расстояния подчиняются неравенству треугольника (4).
Если оно соблюдается, можно предложить несколько алгоритмов с погрешностью 12. Прежде, чем описать такой алгоритм, следует вспомнить старинную головоломку. Можно ли начертить одной линией открытый конверт? Рис.2 показывает, что можно (цифры на отрезках показывают порядок их проведения). Закрытый конверт (рис.3.) одной линией нарисовать нельзя и вот почему. Будем называть линии ребрами, а их перекрестья – вершинами.
Когда через точку проводится линия, то используется два ребра – одно для входа в вершину, одно – для выхода. Если степень вершины нечетна – то в ней линия должна начаться или кончиться. На рис. 3 вершин нечетной степени две: в одной линия начинается, в другой – кончается. Однако на рис. 4 имеется четыре вершины степени три, но у одной линии не может быть четыре конца. Если же нужно прочертить фигуру одной замкнутой линией, то все ее вершины должны иметь четную степень.
Верно и обратное утверждение: если все вершины имеют четную степень, то фигуру можно нарисовать одной незамкнутой линией. Действительно, процесс проведения линии может кончиться, только если линия придет в вершину, откуда уже выхода нет: все ребра, присоединенные к этой вершине (обычно говорят: инцидентные этой вершине), уже прочерчены. Если при этом нарисована вся фигура, то нужное утверждение доказано; если нет, удалим уже нарисованную часть G’. После этого от графа останется одна или несколько связных компонент; пусть G’ – одна из таких компонент. В силу связности исходного графа G, G’ и G” имеют хоть одну общую вершину, скажем, v. Если в G” удалены какие-то ребра, то по четному числу от каждой вершины. Поэтому G” – связный и все его вершины имеют четную степень. Построим цикл в G” (может быть, не нарисовав всего G”) и через v добавим прорисованную часть G” к G’. Увеличивая таким образом прорисованную часть G’, мы добьемся того, что G’ охватит весь G.
Эту задачу когда-то решил Эйлер, и замкнутую линию, которая покрывает все ребра графа, теперь называю эйлеровым циклом. По существу была доказана следующая теорема.
Эйлеров цикл в графе существует тогда и только тогда, когда (1) граф связный и (2) все его вершины имеют четные степени.