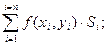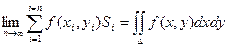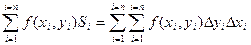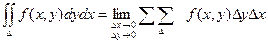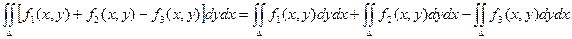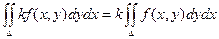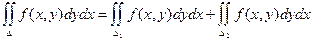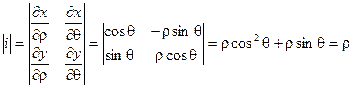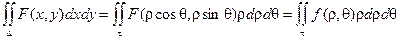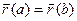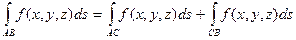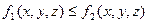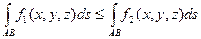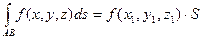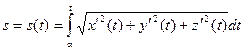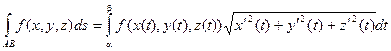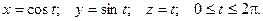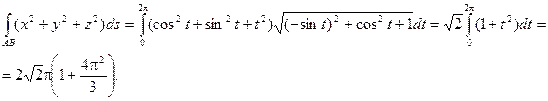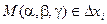Интегральное исчисление функций нескольких переменных

Читайте также:

1. E) Погрешности функций измеренных величин
2. II. Неопределенный интеграл
3. II. Неопределенный интеграл
4. N синтезируется во многих клетках с гена р53
5. АНАЛИЗ ФУНКЦИЙ, ВЫПОЛНЯЕМЫХ ПЕРСОНАЛОМ, И ЗАТРАТ НА ИХ ОСУЩЕСТВЛЕНИЕ
6. Аналитическая запись функций алгебры логики
7. Аналитическое описание булевых функций
8. Аппроксимативные свойства однородных скоростных функций. Геологические среды, которые могут быть приближены однородными функциями.
9. Аппроксимация функций методом наименьших квадратов.
10. Базис И, ИЛИ, НЕ. Свойства элементарных функций алгебры логики
11. В информационной теории эмоций выделяется несколько функций эмоций.
12. В специальной литературе приводится множество определений понятия управления и тех функций, которые присущи этой экономической категории.

Как известно, интегрирование является процессом суммирования. Однако суммирование может производится неоднократно, что приводит нас к понятию кратных интегралов. Рассмотрение этого вопроса начнем с рассмотрения двойных интегралов.

Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой

y

Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой областью D. Если выбрать точки области без учета точек, лежащих на кривой, область будет называется незамкнутой область D.

С геометрической точки зрения D – площадь фигуры, ограниченной контуром.

Разобьем область D на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние Dх_i, а по оси у – на Dу_i. Вообще говоря, такой порядок разбиения наобязателен, возможно разбиение области на частичные участки произвольной формы и размера.

Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны S_i = Dx_i × Dy_i .

В каждой частичной области возьмем произвольную точку Р(х_i, y_i) и составим интегральную сумму

где f – функция непрерывная и однозначная для всех точек области D.

Если бесконечно увеличивать количество частичных областей D_i, тогда, очевидно, площадь каждого частичного участка S_i стремится к нулю.

Определение: Если при стремлении к нулю шага разбиения области D интегральные суммы 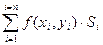имеют конечный предел, то этот предел называется двойным интеграломот функции f(x, y) по области D.

С учетом того, что S_i = Dx_i × Dy_i получаем:

В приведенной выше записи имеются два знака S, т.к. суммирование производится по двум переменным х и у.

Т.к. деление области интегрирования произвольно, также произволен и выбор точек Р_i, то, считая все площади S_i одинаковыми, получаем формулу:

Условия существования двойного интеграла.

Сформулируем достаточные условия существования двойного интеграла.

Теорема. Если функция f(x, y) непрерывна в замкнутой области D, то двойной интеграл существует.

Теорема. Если функция f(x, y) ограничена в замкнутой области D и непрерывна в ней всюду, кроме конечного числа кусочно – гладких линий, то двойной интеграл существует.

Свойства двойного интеграла.

1)

2)

4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования.

5) Если f(x, y) ³ 0 в области D, то .

6) Если f₁(x, y) £ f₂(x, y), то .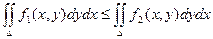

7) .

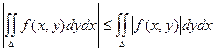
Вычисление двойного интеграла.

Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями х = a, x = b, (a

Воспользуемся формулой замены переменных:

При этом известно, что

В этом случае Якобиан имеет вид:

Тогда

Здесь t – новая область значений,

Определение. Кривая () называется непрерывной кусочно – гладкой, если функции j, y и g непрерывны на отрезке [a,b] и отрезок [a,b] можно разбить на конечное число частичных отрезков так, что на каждом из них функции j, y и g имеют непрерывные производные, не равные нулю одновременно.

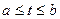
Если определено не только разбиение кривой на частичные отрезки точками, но порядок этих точек, то кривая называется ориентированннойкривой.

Ориетированная кривая называется замкнутой, если значения уравнения кривой в начальной и конечной точках совпадают.

Рассмотрим в пространсве XYZ кривую АВ, в каждой точке которой определена произвольная функция .

Разобьем кривую на конечное число отрезков и рассмотрим произведение значения функции в каждой точке разбиения на длину соответствующего отрезка.

Сложив все полученные таким образом произведения, получим так называемую интегральнуюсумму функции f(x, y, z).

Определение. Если при стремлении к нулю шага разбиения кривой на частичные отрезки существует предел интегральных сумм, то этот предел называется криволинейным интегралом от функции f(x, y, z) по длине дуги АВили криволинейным интегралом первого рода.

Свойства криволинейного интеграла первого рода.

1) Значение криволинейного интеграла по длине дуги не зависит от направления кривой АВ.

2) Постоянный множитель можно выносить за знак криволинейного интеграла.

3) Криволинейный интерал от суммы функций равен сумме криволинейных интегралов от этих функций.

4) Если кривая АВ разбита на дуга АС и СВ, то

5) Если в точках кривой АВ

6) Справедливо неравенство:

7) Если f(x, y, z) = 1, то

S – длина дуги кривой, l – наибольшая из всех частичных дуг, на которые разбивается дуга АВ.

8) Теорема о среднем.

Если функция f(x, y, z) непрерывна на кривой АВ, то на этой кривой существует точка (x₁, y₁, z₁) такая, что

Для вычисления криволинейного интеграла по длине дуги надо определить его связь с обыкновенным определенным интегралом.

Пусть кривая АВ задана параметрически уравнениями x = x(t), y = y(t), z = z(t),

a £ t £ b, где функции х, у, z – непрерывно дифференцируемые функции параметра t, причем точке А соответствует t = a, а точке В соответствует t = b. Функция f(x, y, z) – непрерывна на всей кривой АВ.

Для любой точки М(х, у, z) кривой длина дуги АМ вычисляется по формуле

(См. Вычисление длины дуги кривой.):

Длина всей кривой АВ равна:

Криволинейный интеграл по длине дуги АВ будет находиться по формуле:

Таким образом, для вычисления криволинейного интеграла первого рода (по длине дуги АВ) надо, используя параметрическое уравнение кривой выразить подынтегральную функцию через параметр t, заменить ds дифференциалом дуги в зависимости от параметра t и проинтегрировать полученное выражение по t.

Пример. Вычислить интеграл по одному витку винтовой линии

Если интегрирование производится по длине плоской кривой, заданной уравнением 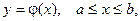то получаем:

Криволинейные интегралы второго рода.

Пусть АВ – непрерывная кривая в пространстве XYZ (или на плоскости ХОY), а точка P(x, y, z) – произвольная функция, определенная на этой кривой. Разобьем кривую точками на конечное число частичных дуг. И рассмотрим сумму произведений значений функции в каждой точке на длину соответствующей частичной дуги.

;

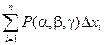
Дата добавления: 2014-01-07 ; Просмотров: 867 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Задача 7. Вычислить .

Решение. Это интеграл вида с чётными m и n (в данном случае ). Воспользуемся формулой (19) понижения степени

,

получим

Интегральное исчисление функций нескольких переменных

Понятие двойного интеграла

Квадрируемые фигуры и их площади

Определение. Плоской фигурой F называется ограниченная замкнутая область из . Множество всех граничных точек фигуры F называется её границей и обозначается .

Определение. Многоугольником называется плоская фигура, ограниченная замкнутой ломаной.

Многоугольная фигура P – объединение нескольких многоугольников.

Понятие площади многоугольной фигуры и её свойства известны (из курса геометрии). Площадь обозначим .

Свойства площади многоугольной фигуры

.

Если , и P1 и P2 не имеют общих внутренних точек, то (аддитивность).

Если P1=P2, то (инвариантность).

Если то (монотонность)

Пусть дана плоская фигура F, ограниченная одной или несколькими замкнутыми кривыми. Рассмотрим всевозможные многоугольные фигуры Р, целиком содержащиеся в F, и многоугольные фигуры Q, целиком содержащие в себе F: . Для их площадей справедливо .

Рассмотрим 2 числовых множества: и . Множество ограничено сверху любым числом из . Следовательно, имеет верхнюю грань, то есть . выполнено . Следовательно, , то есть ограничено снизу. Следовательно, . Ясно, что . Тогда выполнено

.

Определение. Фигура F называется квадрируемой, если . При этом называется площадью фигуры F.

Теорема 1 (необходимое и достаточное условие квадрируемости). Пусть дана произвольная плоская фигура F. Для квадрируемости плоской фигуры F необходимо и достаточно, чтобы , такие, что .

Теорема 2. Фигура F квадрируема, если её границу можно разбить на конечное число частей, каждая из которых представляют собой кривую вида y=f(x), x Î [a;b] или x=φ(y), y Î [c;d], где f и φ – непрерывные функции.

Определение. Кривая L называется гладкой, если он задана параметрическими уравнениями

где определены и непрерывно дифференцируемы на [α;β], и " t Î [α;β].

Кривая называется кусочно-гладкой, если её множество разбить на конечное число гладких кривых.

Теорема 3. Фигура F квадрируема, если её граница является гладкой или кусочно-гладкой кривой.

Площадь плоской фигуры обладает теми же свойствами, что и площадь многоугольной фигуры:

.

Если , и F1 и F2 не содержит общих внутренних точек, то .

Если F1=F2, то .

Если то .

2. Задача об объёме цилиндрического бруса

Пусть тело V ограничено: снизу – плоской фигурой P, лежащей в плоскости XOY, сверху – поверхностью z=f(x;y), где f – неотрицательная и непрерывная на P функция, с боков – цилиндрической поверхностью с образующими параллельными оси OZ. Такое тело называется цилиндрическим брусом. Найдём объём тела V. Разобьём область Р сетью кривых на n частей P1, P2,…,Pn. На контуре каждой части Pk построим поверхность с образующей, параллельной оси OZ. Эта поверхность вырежет в теле столбик Vk с основанием Pk. Таких столбиков будет n, и в совокупности они составят всё тело V. Сумма объёмов всех Vk даст объём тела V. Выберем в каждой части Pk произвольную точку и вычислим в ней значение функции . Затем каждый цилиндрический столбик Vk заменим прямым цилиндром с основанием Pk и высотой zk. Тогда объём цилиндрического столбика Vk приблизительно равен объёму этого прямого цилиндра: .

Просуммировав эти выражения по , получим объём V:

.

Это равенство тем точнее, чем мельче разбиение области P на части Pk.

Диаметром замкнутой области P называется наибольшее расстояние между двумя точками её границы. Пусть -диаметр Pk. Обозначим . Пусть , тогда то есть

.

3. Определение двойного интеграла

Пусть на замкнутой квадрируемой области P задана функция z=f(x;y). Построим разбиение T области P сетью кривых на n частичных квадрируемых областей P1, P2,…,Pn. Площади их также обозначим P1, P2,…,Pn. В каждой из частей Pk произвольно выберем точку и вычислим значение функции в ней. Составим сумму

,

которую будем называть интегральной суммой для функции f(x;y) на области Р, соответствующей разбиению T и выбору точек . Пусть l k – диаметр области Рk, .

Определение 1. Число I называется пределом интегральной суммы S(T) , если для любого разбиения Т области P, такого, что и при любом выборе точек Î Рk выполнено .

Определение 2. Если существует конечный предел интегральной суммы S(T) при , не зависящий ни от способа разбиения T, ни от выбора точек , то этот предел называется двойным интегралом от функции f(x;y) по области P и обозначается или ,

где dP – элемент площади.

Итак, .

Функция f(x;y) в этом случае называется интегрируемой на области P.

Геометрический смысл двойного интеграла

1) Рассматривая задачу об объёме цилиндрического бруса, мы установили что . Мы предполагали, что f-непрерывная функция. Так как справа мы имеем предел интегральной суммы S(T) для непрерывной функции, то он существует и равен двойному интегралу от этой функции по области P. Значит, .

Двойной интеграл от неотрицательной непрерывной функции геометрически выражает объем цилиндрического бруса.

2) Если положить f(x;y)=1 всюду в области P, то

,

– площадь плоской фигуры равна двойному интегралу от 1 по этой области.

5. Ограниченность интегрируемой функции

Теорема 1. Если функция z= f(x;y) интегрируема на области Р, то она ограничена на ней.

Допустим, что функция не ограничена на области Р. Тогда при любом разбиении области на части функция будет не ограничена хотя бы в одной из её частей. Тогда, выбирая точку произвольно, мы можем сделать сколь угодно большим. Значит, и интегральная сумма S(T) будет сколь угодно большой по абсолютной величине. Следовательно, S(T) не будет иметь конечного предела, и поэтому функция f(x;y) не будет интегрируемой.

Замечание. Обратное утверждение неверно.

Функции нескольких переменных

При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.

Определение: Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому – либо правилу ставится в соответствие одно или несколько значений переменной z , то переменная z называется функцией двух переменных.

Определение: Если паре чисел (х, у) соответствует одно значение z , то функция называется однозначной, а если более одного, то – многозначной. Векторный анализ Задача. Найти производную скалярного поля

Определение: Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.

Определение: Окрестностью точки М(х, у) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию .

Определение: Число А называется пределом функции f ( x , y ) при стремлении точки М(х, у) к точке М(х, у), если для каждого числа e > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие

также верно и условие .

Записывают:

Определение: Пусть точка М(х, у) принадлежит области определения функции f ( x , y ). Тогда функция z = f ( x , y ) называется непрерывной в точке М(х, у), если

(1)

причем точка М(х, у) стремится к точке М(х, у) произвольным образом.

Если в какой – либо точке условие (1) не выполняется, то эта точка называется точкой разрыва функции f ( x , y ). Это может быть в следующих случаях :

1) Функция z = f ( x , y ) не определена в точке М(х, у).

2) Не существует предел .

3) Этот предел существует, но он не равен f ( x , y ).

Свойство. Если функция f ( x , y , …) определена и непрерывна в замкнутой и

ограниченной области D , то в этой области найдется по крайней мере одна точка

N ( x , y , …), такая, что для остальных точек верно неравенство

а также точка N ₁ ( x ₀₁ , y ₀₁ , …), такая, что для всех остальных точек верно неравенство

тогда f ( x , y , …) = M – наибольшее значение функции, а f ( x ₀₁ , y ₀₁ , …) = m – наименьшее значение функции f ( x , y , …) в области D .

Непрерывная функция в замкнутой и ограниченной области D достигает по крайней мере один раз наибольшего значения и один раз наименьшего.

Свойство. Если функция f ( x , y , …) определена и непрерывна в замкнутой ограниченной области D , а M и m – соответственно наибольшее и наименьшее значения функции в этой области, то для любой точки m Î [ m , M ] существует точка

Пяяще говоряя непрерывная функция принимает в области D все промежуточные значения между M и m . Следствием этого свойства может служить заключение, что если числа M и m разных знаков, то в области D функция по крайней мере один раз обращается в ноль.

Свойство. Функция f ( x , y , …), непрерывная в замкнутой ограниченной области D , ограничена в этой области, если существует такое число К, что для всех точек области верно неравенство

Свойство. Если функция f ( x , y , …) определена и непрерывна в замкнутой ограниченной области D , то она равномерно непрерывна в этой области, т.е. для любого положительного числа e существует такое число D > 0, что для любых двух точек (х₁, y ₁ ) и (х₂, у₂) области, находящихся на расстоянии, меньшем D , выполнено неравенство

Приведенные выше свойства аналогичны свойствам функций одной переменной, непрерывных на отрезке.

Элементы дискретной математики Элементы математической логики, теории множеств и общей алгебры. Дискретные объекты и структуры в математике. Метод математической индукции. Бинарные и n-арные отношения. Необходимые и достаточные условия. Логические (булевы) переменные. Алгебра логики, функции алгебры логики (булева алгебра, булевы функции). Множества, отображения, мощности. Алгебра множеств. Дизъюнктивные и конъюнктивные нормальные формы. Минимизация булевых функций. Функциональная полнота систем булевых функций. Понятие группы. Абелева группа. Подгруппы. Циклическая группа. Изоморфизмы, автоморфизмы, гомоморфизмы. Кольца, тела и поля.