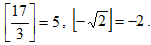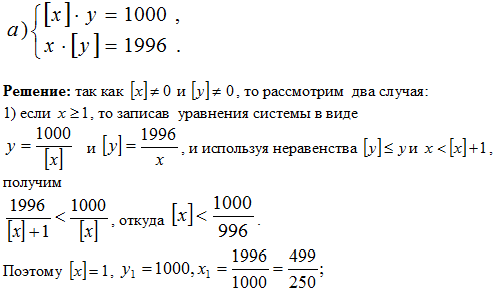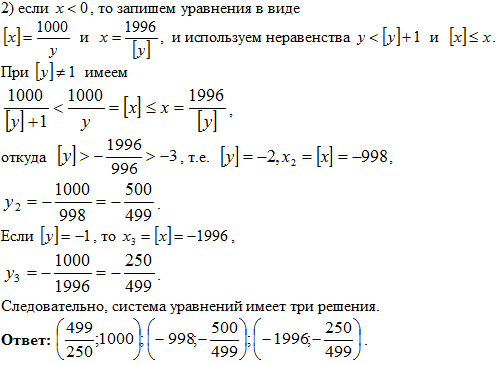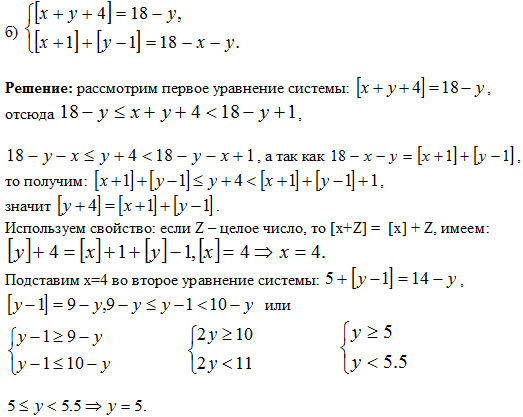Задачи на целую и дробную часть

Разделы: Математика

Цели урока: познакомить учащихся с понятием целой и дробной части числа; сформулировать и доказать некоторые свойства целой части числа; познакомить учащихся с широким спектром применения целой и дробной части числа; совершенствовать умение решать уравнения и системы уравнений, содержащих целую и дробную части числа.

Оборудование: плакат “Кто смолоду делает и думает сам, тот и становится потом надёжнее, крепче, умнее” (В. Шукшин).
Проектор, магнитная доска, справочник по алгебре.

1. Организационный момент.
2. Проверка домашнего задания.
3. Изучение нового материала.
4. Решение задач по теме.
5. Итоги урока.
6. Домашнее задание.

I. Организационный момент: сообщение темы урока; постановка цели урока; сообщение этапов урока.

II. Проверка домашнего задания.

Ответить на вопросы учащихся по домашнему заданию. Решить задачи, вызвавшие затруднения при выполнении домашней работы.

III. Изучение нового материала.

Во многих задачах алгебры приходится рассматривать наибольшее целое число, не превосходящее данного числа. Такое целое число получило специальное название “целая часть числа”.

Целой частью действительного числа х называется наибольшее целое число, не превосходящее х. Целая часть числа х обозначается символом [x] или Е(х) (от французского Entier “антье” ─ “целый”). Например, [5] = 5, [ π ] = 3,

Из определения следует, что [x] ≤ х, так как целая часть не превосходит х.

С другой стороны, т.к. [x] – наибольшее целое число, удовлетворяющее неравенству, то [x] +1>х. Таким образом, [x] есть целое число, определяющееся неравенствами [x] ≤ х α = υ ─ [x] называют дробной частью числа х и обозначают <х>. Тогда имеем: 0 ≤ <х>0 ≤ α о [x+у] = [x] + [у].

Если 1≤ α т.е. α = 1 + α` , где 0 ≤ α` α` и

Это свойство распространяется на любое конечное число слагаемых:

Умение находить целую часть величины очень важно в приближенных вычислениях. В самом деле, если мы умеем находить целую часть величины х, то, приняв [x] или [x]+1 за приближенное значение величины х, мы сделаем погрешность, величина которой не больше единицы, так как

≤ х – [x] ≥ 0 , а во-вторых, в сумме, стоящей в середине полученного двойного неравенства, все слагаемые, начиная с третьего, равны 0, так что x .

Поскольку х – целое число, то остается проверить значения от 0 до 6. Решениями уравнения оказываются числа 0,4 и 5.

Задача 7. Решить систему уравнение

(Провести проверку с помощью проектора.)

Найти число корней уравнения

Преобразуем, неравенство к виду 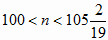, откуда получим, что искомое количество целых чисел равно 5. Значит, число корней данного уравнения равно 5.

Задача 9. (Соросовская олимпиада).

а) провести проверку самостоятельных работ с помощью проектора;

б) ответить на вопросы:

1. “Дайте определение целой и дробной части числа”;
2. “При решении, каких задач используется целая и дробная часть числа?”;

в) выставление отметок.

VI. Домашнее задание.

Дополнительная задача (по желанию).

Некто измерил длину и ширину прямоугольника. Он умножил целую часть длины на целую часть ширины и получил 48; умножил целую часть длины на дробную часть ширины и получил 3,2; умножил дробную часть длины на целую часть ширины и получил 1,5. Определите площадь прямоугольника.

Изучая алгебру 10 класса по учебнику А.Г.Мордковича и П.В. Семёнова, ученики впервые встретились с функцией целой части числа у = [х]. Некоторых она заинтересовала, но теоретических сведений, да и заданий, содержащих целую часть числа, оказалось очень мало. Чтобы поддержать интерес детей к предмету и возникла идея создания данного пособия.

Реализация программы курса рассчитана на 1 полугодие 10 класса для обучающихся физико – математического профиля.

Цель курса: расширить знания обучающихся о математических функциях и формировать умение использовать знания о функциях при решении уравнений и неравенств разной степени сложности. В представленном учебном пособии содержатся теоретические сведения справочного характера. Это сведения о функции целой части числа у = [х] и функции дробной части числа у = <х>, их графиках. Объясняются преобразования графиков, содержащих целую часть числа. Рассмотрены решения простейших уравнений и неравенств, содержащих целую или дробную частъ числа. А также методы решения квадратных, дробно – рациональных уравнений и неравенств, систем уравнений, содержащих целую или дробную часть числа.

В пособии приведены задания для самостоятельного решения.

Пособие включает в себя следующие пункты:

§1. Знакомство с функциями у = [х] и у =<х>.

§2. Уравнения, содержащие дробную или целую часть числа.

2.1 Простейшие уравнения.

2.2 Решение уравнений вида [f (х)] = g (х).

2.3 Графический способ решения уравнений.

2.4 Решение уравнений введением новой переменной.

2.5 Системы уравнений.

§3. Преобразование графиков функций, содержащих целую часть числа.

3.1 Построение графиков функций вида у = [f (х)]

3.2 Построение графиков функций вида у = f ([х]).

§4. Неравенства, содержащие целую или дробную часть числа.

§5. Целая и дробная часть числа в олимпиадных заданиях.

Ответы на задания для самостоятельного решения.

Пособие обеспечивает развитие представлений о функции и формирование прикладных навыков.

Адресовано учителям, решающим задачи профильного обучения.

Скачать:

Вложение	Размер
uchebnoe_posobie_zadachisoderzhashchie_celuyu_ili_drobnuyu_chast_chisla.doc	822.5 КБ

Предварительный просмотр:

Задачи, содержащие целую

или дробную часть числа

Вы приступаете к углубленному изучению темы «Целая и дробная части числа». Данное пособие позволит вам расширить свои знания о математических функциях при решении уравнений и неравенств разной степени сложности. В представленном пособии содержатся теоретические сведения справочного характера, объясняются преобразования графиков, содержащих целую или дробную часть числа, рассмотрены решения простейших уравнений. А также методы решения квадратных, дробно – рациональных уравнений и неравенств, систем уравнений. В пособии приведены задания для самостоятельного решения. Учебное пособие поможет вам систематизировать и обобщить полученные знания по теме «Целая и дробная части числа».

§1. Знакомство с функциями у = [х] и у=<х>………………………4

§2. Уравнения, содержащие целую или дробную часть числа…. 7

2.3 Графический способ решения уравнений………………10

1. Решение уравнений введением новой переменной……11

§3. Преобразования графиков функций, содержащих целую

1. 3.1 Построение графиков функций вида у = [f(х)]……………13
2. 3.2 Построение графиков функций вида у = f([х])……………15

§4. Неравенства, содержащие целую или дробную часть числа. 17

§5. Целая или дробная часть числа в олимпиадных заданиях…. 20

Ответы на задания для самостоятельного решения……………. 23

§1. Знакомство с функциями у = [x]

История и определение целой и дробной части числа

Понятие целой части числа было введено немецким математиком Иоганном Карлом Фридрихом Гауссом(1771-1855), автором "Трудов по теории чисел". Также Гаусс продвинул теорию специальных функций, рядов, численные методы, решение задач математической физики, создал математическую теорию потенциала.

Обозначается целая часть действительного числа x символом [x] или E(x).

Символ [x] был введён К.Гауссом в 1808 г.

Функция же целой части числа была введена Адриеном Мари Лежандром ( 1752-1833). – французским математиком. Его работа "Опыт теории чисел", которая вышла в свет в 1798 году, является фундаментальным трудом, итогом арифметических достижений XVIII века. Именно в честь него функцию y = [x] называют французским словом "Антье" (фр. «entier» -целый) обозначают E(x).

Определение: целой частью числа х называется наибольшее целое число с, не превышающее х, т.е. если [х] = с, c ≤ x

По некоторым значениям функции можно построить её график. Он выглядит следующим образом:

Свойства функции y = [x]:

1. Область определения функции y = [x] есть множество всех действительных чисел R.

2. Область значений функции y = [x] есть множество всех целых чисел Z.

3. Функция y = [x] кусочно-постоянная, неубывающая.

4. Функция общего вида.

5. Функция не периодична.

6. Функция не ограничена.

7. Функция имеет точку разрыва.

9. y 0, при х 0,при х>0.

10.Функция не имеет точек экстремума.

11. У наиб. и У наим. не существует.

Возникает вопрос: «Если есть функция целой части числа, может, есть и функция дробной части числа?»

Определение: дробная часть числа (обозначается <х>) есть разность х – [х].

Построим график функции у = <х>. Он выглядит следующим образом:

Простейшие свойства функции y = :

1. Область определения функции y = есть множество всех действительных чисел R.

2. Область значений функции y = есть полуинтервал [0;1)

3.Функция общего вида.

5.Функция не прерывна.

6.у=0, при всех целых х.

7.у>0, при всех действительных х.

8.Функция монотонно возрастает на [n; n+1)

9. Функция не имеет точек экстемума.

Представление о том, как выглядят графики функций у = [х] и у = <х>поможет выполнить и некоторые задания.

ЗАДАНИЯДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1) Построить графики функций:

2) Какими могут быть числа х и у, если:

3) Что можно сказать о величине разности х – у , если:

4) Что больше: [а] или <а>?

§2. Уравнения, содержащие целую или дробную часть числа

2.1. Простейшие уравнения

К простейшим уравнениям относятся уравнения вида [х] = а.

Уравнения такого вида решаются по определению:

Если а – дробное число, то такое уравнение не будет иметь корней.

Рассмотрим пример решения одного из таких уравнений:

[х + 1,3] = – 5. По определению такое уравнение преобразуется в неравенство:

Это и будет являться решением уравнения.

Рассмотрим ещё одно уравнение, относящееся к разряду простейших:

Для решения уравнений такого вида необходимо использовать свойство функции целого числа: Если р – целое число, то справедливо равенство

Доказательство: х = [х] +

х = k + а, где k = [х], а =

[ k + a ± p ] = [ k + a ] ± p = [х] ±p.

Решим предложенное уравнение, используя доказанное свойство: Получим [х] + 1 + [х] – 2 – [х] – 3 = 2. Приведём подобные слагаемые и получим простейшее уравнение [х] = 6. Его решением является полуинтервал х[6;7), который и будет решением данного уравнения.

Рассмотрим более сложное уравнение:

Преобразуем уравнение в неравенство: 1 ≤ х 2 -5х+6

х 2 – 5х + 6 ≥ 1 и решим её;

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

3) [x + 4] – [x + 1] = 2

2.2 Решение уравнений вида [f(x)]=g(x)

Уравнение вида [f(x)]=g(x) можно решить путем сведения их к уравнению

Рассмотрим пример 1 .

Заменим правую часть уравнения на новою переменную a и выразим отсюда x

11a = 16x + 16, 16x = 11a – 16,

Теперь решим уравнение относительно переменной а .

Раскроем знак целой части по определению и запишем с помощью системы неравенств:

Из промежутка выберем все целые значения a: 3;4;5;6;7 и проведем обратную замену:

Разделим каждое слагаемое числителя в скобке на знаменатель:

Из определения целой части числа следует, что (а+1) должно быть целым, значит и а – целое. Числа а, (а+1), (а+2) – три последовательных числа, значит одно из них обязательно делится на 2, а одно – на 3. Следовательно, произведение чисел делится нацело на 6.

То есть целое число. Значит

Решим это уравнение.

а + 1 = 0 или а 2 + 2а – 6 = 0

a = -1 ± (не являются целыми).

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:

2.3. Графический способ решения уравнений

Решение. Решим это уравнение графически. Построим графики функций у = [х] и у = 2<х>. Найдём абсциссы точек их пересечения.

Ответ: х = 0; х = 1,5.

В некоторых случаях удобнее по графику найти ординаты точек пересечения графиков. Затем подставить полученное значение в одно из уравнений и найти искомые значения х.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Решите уравнения графически:

10) Сколько решений имеет уравнение 2 <х>= 1 – .

2.4. Решение уравнений введением новой переменной.

Рассмотрим первый пример:

Заменим <х>на а, 0 а

а 2 – 8а + 7 = 0, которое решим по теореме, обратной теореме Виета: Полученные корни а = 7 и а = 1 . Проведем обратную замену и получим два новых уравнения: <х>= 7 и <х>= 1. Оба эти уравнения не имеют корней. Следовательно, уравнение не имеет решений.

Ответ: решений нет.

Рассмотрим ещё один случай решения уравнения введением новой

3[х] 3 + 2[х] 2 + 5[х]-10 = 0

Проведём замену [х] = а, аz. и получим новое кубическое уравнение За 3 +2а 2 +5а-10=0. Первый корень этого уравнения найдём путём подбора: а=1 – корень уравнения. Делим наше уравнение на (а-1). Получаем квадратное уравнение 3а 2 + 5а +10=0. Это уравнение имеет отрицательный дискриминант, а значит, не имеет решений. То есть, а=1 – единственный корень уравнения. Проводим обратную замену: [х]=а=1. Полученное уравнение решаем по определению целой части числа: х[1 ;2).

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:

10) 10[х] 3 -11[х] 2 -31[х]-10 = 0

2.5. Системы уравнений.

Рассмотрим систему уравнений:

Ее можно решить либо методом сложения, либо подстановкой. Остановимся на первом способе.

После сложения двух уравнений получаем 11[x] = 11. Отсюда

[x] = 1. Подставим это значение в первое уравнение системы и получаем

[x] = 1 и [y] = 2 – решения системы. То есть x [1;2), y [2;3).

Ответ: ( x [1;2), y [2;3)).

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:

§3. Преобразования графиков функций, содержащих целую часть числа

3.1. Построение графиков функции вида y = [f(x)]

Пусть имеется график функции у = f(х). Чтобы построить график функции у = [f(x)], поступаем следующим образом:

1. Проводим прямые у = n, n = 0; -1; +1; -2; +2; … и рассматриваем одну из полос, образованных прямыми у = n, у = n + 1.
2. Отмечаем точки пересечения прямых у = n, у = n + 1 с графиком функции у = f(х). Эти точки принадлежат графику функции у = [f(x)], так как их ординаты целые числа (на рисунке это точки А, В, С, D).

1. Для получения остальных точек графика функции у = [f(x)] в указанной полосе часть графика у = f(х), попавшую в полосу, проектируем параллельно оси Оу на прямую у = n. Поскольку любая точка М этой части графика функции у = f(х) имеет такую ординату , что n ≤ ] = n.
2. В каждой другой полосе, где имеются точки графика функции у = f(х), построение проводится аналогично.

Построим график функции у = [х]. Для этого

1. Проводим прямые у = n, n = 0; -1; +1; -2; +2; … и рассматриваем одну из полос, образованных прямыми у = n, у = n + 1.
2. Отмечаем точки пересечения прямых у = n, у = n + 1 с графиком

функции у = [х]. Эти точки принадлежат графику функции у = [х],

так как их координаты целые числа.

1. Для получения остальных точек графика функции у = [х] в указанной полосе часть графика у = х, попавшую в полосу, проецируем параллельно оси О у на прямую у = n, у = n + 1. Поскольку любая точка М этой части графика функции y = x, имеет такую ординату y 0 , что n 0 0 ] = n
2. В каждой другой полосе, где имеются точки графика функции у = х, построение проводится аналогично.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Постройте графики функций:

1. у = ;
2. у = 2[sinx];
3. y = [3 – 1] + 3;
4. у = -[cosx] + 1;
5. y = [|x|];
6. y = [tgx];
7. y = 2[|cosx|] – 4;
8. y = 1,5[cosx] – 2;
9. y = [ctgx + 2] -1

3.2. Построение графиков функции вида y = f([x])

Пусть дан график некоторой функции у = f(х). Построение графика функции у = f([х]) осуществляется следующим образом:

1. Проводим прямые х = n, n = 0; -1; +1; -2; +2; …
2. Рассмотрим одну из полос, образованных прямыми у = n и у = n + 1. Точки А и В пересечения графика функции у = f(х) с этими прямыми принадлежат графику функции у = f([х]), так как их абсциссы – целые числа.

1. Для получения остальных точек графика функции у = f([х]) в указанной полосе часть графика функции у = f(х), попавшую в эту полосу, проектируем параллельно оси О у на прямую у = f(n).
2. В каждой другой полосе, где имеются точки графика функции у = f(х), построение ведётся аналогично.

Рассмотрим построение графика функции у = . Для этого пунктиром построим график функции у = . Далее

1. Проводим прямые х = n, n = 0; -1; +1; -2; +2; …
2. Рассмотрим одну из полос, образованных прямыми у = n и у = n + 1. Точки пересечения графика функции у = с этими прямыми принадлежат графику функции у = , так как их абсциссы – целые

3. В каждой другой полосе, где имеются точки графика функции у = , построение ведётся аналогично.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Постройте графики функций:

§4. Неравенства, содержащие целую или дробную части числа

Назовём основными неравенствами с [х] и <х>следующие соотношения: [х] > b и <х>> b. Удобным методом их решения является графический метод. Поясним его на двух примерах.

Решение. Введём в рассмотрение две функции у = [х] и у = b и начертим их графики на одном и том же чертеже. Ясно, что тогда следует различать два случая: b – целое и b – нецелое.

Случай 1. b – целое

Из рисунка видно, что графики совпадают на [b; b + 1].

Следовательно, решением неравенства [х] ≥ b будет луч х ≥ b.

Случай 2. b – нецелое.

В этом случае графики функций у = [х] и у = b не пересекаются. Но часть графика у = [х], лежащая выше прямой, начинается в точке с координатами ([b] + 1; [b] + 1). Таким образом, решением неравенства [х] ≥ b будет луч х ≥ [b] + 1.

Остальные виды основных неравенств исследуются точно так же. Результаты этих исследований сведены ниже в таблицу.

Идёт приём заявок

Подать заявку

Для учеников 1-11 классов и дошкольников

История и определение целой и дробной части числа

В эпоху Средневековья жил один из величайших английских учёных монах – францисканец Уильям Оккам. Он родился в Оккаме, английском графстве Серрей, где – то между 1285 и 1300 годами, учился и преподавал в Оксфорде, а затем в Париже. Преследуемый из-за своего учения, Оккам нашел себе убежище при дворе Людовика IV Баварского в Мюнхене и, благоразумно не покидая его, прожил там вплоть до своей кончины в 1349 г.

Оккама считают одним из предшественников великих мыслителей Рене Декарта и Иммануила Канта. Согласно его философским воззрениям, реальность есть бытие конкретной вещи, поэтому «тщетно делать с большим то, что можно делать с меньшим». Это высказывание стало основой принципа экономии мышления. Уильям Оккам применял его с такой разящей силой, что он получил впоследствии столь популярное сейчас название «бритвы Оккама».

Для многих людей, не сведущих в математике, общим местом стали вопросы типа «Что же ещё можно открыть в математике?». Учитывая математическую подготовленность спрашивающих, можно предположить, что речь идёт только о математике школьного уровня. Вполне в духе Оккама мы предлагаем вопрошающим, и в первую очередь самим учащимся, некоторые задачи, варьирующие хорошо знакомые им понятия целой и дробной частей числа. На этих задачах мы покажем, как важно рассматривать не каждую задачу в отдельности, а соединять их в систему, разрабатывая общий алгоритм решения. Такой методический приём диктует нам принцип экономии мышления Оккама.

Определение: целой частью числа х называется наибольшее целое число с, не превышающее х, т.е. если [х] = с, c ≤ x c + 1.

Обозначается целая часть действительного числа x символом [x] или E(x).

Символ [x] был введён немецким математиком К. Гауссом (1771-1855) в 1808 г. для обозначения целой части числа x .

Функцию у = [х] называют функцией «Антье» ( фр. e ntier – целый) и обозначается E(x). Этот знак предложил в 1798 году французский математик А.Лежандр (1752-1833) . По некоторым значениям функции можно построить её график. Он выглядит следующим образом:

Простейшие свойства функции y = [x]:

1. Область определения функции y = [x] есть множество всех действительных чисел R.

2. Область значений функции y = [x] есть множество всех целых чисел Z .

3. Функция y = [x] кусочно-постоянная.

4. Функция y = [x] неубывающая, т. е. для любых х ₁ и х ₂ из R таких,

что х ₁ ≤ х ₂ ,имеет место неравенство [ х ₁ ] ≤ [ х ₂ ].

5. Для любого целого числа n и любого действительного числа x выполняется равенство: [x + n] = [x] + n.

6. Если х ─ нецелое действительное число, то справедливо следующее равенство [-x] = -[x] – 1.

7. Для любого действительного числа х верно соотношение

[x] ≤ x ─ целое число, т. е. х Z.

Возникает вопрос: «Если есть функция целой части числа, может, есть и функция дробной части числа?»

Определение: дробная часть числа (обозначается <х>) есть разность х – [х].

Построим график функции у = <х>. Он выглядит следующим образом:

Простейшие свойства функции y = :

1. Область определения функции y = есть множество всех действительных чисел R.

2. Область значений функции y = есть полуинтервал [0;1).

3. Функция y = ограничена, т. е. для любого действительного числа x имеет место соотношение: 0 ≤

4. Для любого целого числа n и любого действительного числа х выполняется равенство: = , т. е. функция y = – периодическая с основным периодом, равным единице.

5. Если х ― нецелое действительное число, то справедливо равенство: <-x>= 1 – .

Представление о том, как выглядят графики функций у = [х] и у = <х>поможет выполнить и некоторые задания.

1) Построить графики функций:

2) Какими могут быть числа х и у, если:

3) Что можно сказать о величине разности х – у , если:

4) Что больше: [а] или <а>?

2.1. Простейшие уравнения

К простейшим уравнениям относятся уравнения вида [х] = а.

Уравнения такого вида решаются по определению:

Если а – дробное число, то такое уравнение не будет иметь корней.

Рассмотрим пример решения одного из таких уравнений:

[х + 1,3] = – 5. По определению такое уравнение преобразуется в неравенство:

Это и будет являться решением уравнения.

Ответ: х[-6,3;-5,3).

Рассмотрим ещё одно уравнение, относящееся к разряду простейших:

Для решения уравнений такого вида необходимо использовать свойство функции целого числа: Если р – целое число, то справедливо равенство

Доказательство: х = [х] +

х = k + а, где k = [х], а =

[ k + a ± p ] = [ k + a ] ± p = [х] ± p .

Решим предложенное уравнение, используя доказанное свойство: Получим [х] + 1 + [х] – 2 – [х] – 3 = 2. Приведём подобные слагаемые и получим простейшее уравнение [х] = 6. Его решением является полуинтервал х[6;7), который и будет решением данного уравнения.

Ответ: х[6;7).

Рассмотрим более сложное уравнение:

Преобразуем уравнение в неравенство: 1 ≤ х 2 -5х+6

х 2 – 5х + 6

х 2 – 5х + 6 ≥ 1 и решим её;

Получаем х(1;4)

х(-∞;(5 – )/2][(5 +)/2; +∞),

х(1; (5 – )/2][(5 +)/2;4).

Ответ: х(1; (5 – )/2][(5 +)/2;4).

РЕШИТЕ ПРЕДЛОЖЕННЫЕ УРАВНЕНИЯ САМОСТОЯТЕЛЬНО: